 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Одномерное движение газаСтр 1 из 3Следующая ⇒
ИЗУЧЕНИЕ ПРОЦЕССА АДИАБАТНОГО ИСТЕЧЕНИЯ ГАЗА ЧЕРЕЗ СУЖИВАЮЩЕЕСЯ СОПЛО ЛАБОРАТОРНАЯ РАБОТА № 5 ИЗУЧЕНИЕ ПРОЦЕССА АДИАБАТНОГО ИСТЕЧЕНИЯ ГАЗА ЧЕРЕЗ СУЖИВАЮЩЕЕСЯ СОПЛО
ЦЕЛЬ РАБОТЫ: · Экспериментальное изучение процесса адиабатного истечения воздуха через суживающееся сопло; · Опытное определение зависимости скорости и расхода газа через суживающееся сопло, коэффициента расхода и коэффициента скорости сопла от величины перепада давлений на его входе и выходе. ТЕОРЕТИЧЕСКИЕ СВЕДЕНИЯ: Жидкости и газы, в отличие от твердых тел, обладают относительно слабыми межмолекулярными связями. Эта особенность их физической природы проявляется в легкой подвижности, т. е. текучести (малой сопротивляемости деформации сдвига): движение жидкостей и газов под действием различных сил сопровождается изменением формы, а в общем случае – и объема выделенной ее части. Газы, в отличие от жидкостей, характеризуются проявлением сжимаемости: их плотность является переменной величиной; поверхности свободного уровня они не образуют. Часто газы называют сжимаемыми жидкостями. Вместе с тем, при малых перепадах давления сжимаемость газов проявляется слабо. Подчеркнем, что при больших перепадах давления сжимаемость обнаруживается и в жидкостях, однако, она по сравнению с газами несоизмеримо мала. Отсюда следует, что сжимаемость свойственна всем жидкостям и газам, однако ее количественное проявление различно, в зависимости от физических свойств среды. Это послужило основанием объединить сплошные среды, обладающие общим свойством легкой подвижности, под общим названием жидкости, выделяя практически несжимаемые (капельные) и сжимаемые (газообразные) жидкости. Поэтому в дальнейшем, и мы будем понимать под жидкостью всякую непрерывную среду, обладающую свойством текучести; несжимаемой жидкостью будем называть капельную жидкость или газ, зависимостью плотности которого от давления можно пренебречь, а сжимаемой жидкостью – газ, зависимостью плотности которого от давления пренебречь нельзя. Плотностью r, кг/м3, называется, как известно, ее масса m, заключенная в единице объема V: r = m / V. Для определения плотности, в точке пользуются формулой Величину, обратную плотности, называют удельным объемом: 1/r = u. В общем случае плотность является функцией координат и времени, т.е. r = r (x, y, z, t). В практических приложениях часто используется понятие объемный вес, Н/м3, – вес G, приходящийся на единицу объема V: g = G / V. Для определения объемного веса в данной точке следует пользоваться формулой
Так как G = mg, то плотность и объемный вес связаны между собой соотношением g =rg. (1) Плотность, а, следовательно, и объемный вес меняются с изменением давления и температуры.
Одномерное движение газа Как известно из курса термодинамики, основные параметры состояния газа – давления p, плотность ρ и абсолютная температура T, связаны для идеальных газов уравнением состояния pV = R0Tm/m, (2) где V – объем газа; m – его масса; m – молярная масса газа, (кг/моль); R0 – универсальная газовая постоянная (R0 = 8,314 Дж/(моль·K)). Если учесть, что удельный объем u газа определяется как V/m и равен 1/r, а R0/m = R – газовая постоянная данного газа (Дж/(кг×K)), то уравнение состояния записывается также в форме: pu = RT или p = rRT. (3) Газовая постоянная R кислорода равна 259,81 Дж/(кг·K), углекислого газа – 188,95 Дж/(кг·K), воздуха Rв – 287,1 Дж/(кг·K); R = Rв/D (D – относительная плотность газа по воздуху, равна отношению rг/rв плотности rг газа к плотности rв воздуха при одинаковых (например, стандартных) условиях, причем (rв)ст » 1,204 кг/м3). В термодинамике обычно рассматривают следующие характерные процессы изменения состояния газа: изобарный p = const; изохорный V = const; изотермический pV = const или p/r = const; адиабатический pVk = const, где k = сp/сV – показатель адиабаты, определяемый отношением теплоемкостей при постоянном давлении (сp) и объеме (сV); для воздуха и двухатомных газов k = 1,4, для перегретого водяного пара k = 1,33, для идеального газа сp – сV = R; политропический pVn = const, где n – некоторая постоянная величина. При решении большинства задач газодинамики, процессы изменения состояния газа можно считать изотермическими, адиабатическими, или, в общем случае, – политропическими. Так, например, движение газа в длинной трубе без теплоизоляции стенок можно рассматривать как изотермическое (длительный контакт со стенками трубы приводит к тому, что температура газа не отличается от температуры стенки); истечение газа из отверстия в резервуаре можно (без существенной погрешности) считать происходящим без теплообмена между выходящим газом и внешней средой, т.е. адиабатическим. При адиабатическом процессе давление и плотность связаны соотношением: p/rk = const или p/p0 = (r/r0)k, (4) а, используя уравнение состояния (2), можно получить для данного процесса следующие соотношения:
Для политропического процесса k в выражениях (5) заменяется n. Газовая динамика изучает течения газа с большими скоростями, сравнимыми со скоростью звука (а), изменение скорости при которых приводит к изменению плотности. Процесс измерения параметров газа в звуковой волне, которая представляет собой распространяющиеся в газе слабые возмущения давления и плотности, следует считать адиабатическим. Для определения скорости звука используют следующую формулу:
В частности, для воздуха, подставляя величины k и R, имеем a = 20,1×T1/2. При температуре 15°C последняя формула дает a = 340 м/с. Скорость звука – одна из важнейших механических характеристик газа. Законы его движения резко отличаются в зависимости от соотношения скорости газа u и скорости звука a. Отношение M = u/a (7) называют числом Маха. Течения, в которых u < a и M < 1, называются дозвуковыми. Если u > a и Μ > 1, течение – сверхзвуковое.
Поиск по сайту: |
 .
. .
. . (5)
. (5)
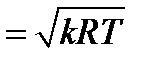 . (6)
. (6)