 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Дисперсия дифференцируемой функции случайного вектора
Для дифференцируемой функции случайного вектора Z = f(X1, X2, …,Xn) (118) связь между ее дисперсией σZ2 и элементами ковариационной матрицы KX её случайных аргументов X1nT может быть установлена лишь приближенно. Однако, при малых по модулю центрированных значениях случайных аргументов Дано: Z = f(Xn1) = f(X1, X2, …,Xn) – дифференцируемая функция случайного вектора Xn1; KX= {Kij} – ковариационная матрица этого вектора, элементы которой Kij определяются формулой (100). Найти: D(Z) = Решение: Представим в формуле (118) каждую случайную величину Xi в виде суммы её математического ожидания и соответствующего центрированного значения Z = f(E(X1) + Разложим дифференцируемую функцию f в ряд Тейлора в окрестности точки E(X1nT), ограничиваясь только линейными членами: Z ≈ f(E(X1) … E(Xn)) + (∂f/∂x1) ∙ Отсюда, переходя к математическому ожиданию функции Z, получаем: E(Z) ≈ f(E(X1), … , E(Xn)), (120) так как E( Центрированное значение Ż величины Z будет линейной функцией центрированных значений её аргументов Ż= Z – E(Z) ≈ (∂f/∂x1)∙ Численные значения частных производных (∂f/∂xi) находят в окрестности точки разложения E(X1nT), где и вычисляется искомая дисперсия. Окончательно, применяя к функции (121) формулу (115) и учитывая, что по третьему свойству дисперсии (60)
имеем:
Полученная формула упрощается для попарно некоррелированных аргументов:
2.3.5.5 Определение дисперсий некоррелированных аргументов по дисперсии функции этих аргументов. Сформулированная в заголовке данного параграфа задача имеет множество решений, так как в одном уравнении (123) мы имеем nнеизвестных дисперсий σi2. Для выбора единственного решения требуются дополнительные ограничения, удовлетворяющие нас по каким-либо мотивам. Во-первых, очевидно, что все решения должны быть положительными, т.е. они не должны противоречить определению дисперсии. Во-вторых, ограничения можно сформулировать, опираясь на здравый смысл. Рассмотрим наиболее простые и практически обоснованные варианты ограничений: «принцип равных дисперсий», «принцип равных влияний» и «принцип имеющихся возможностей». Принцип равных дисперсий. Данный принцип используется в ситуации, когда аргументы Xi являются физически однородными величинами и для их измерений предполагается использование однотипной технологии, характеризующейся постоянной дисперсией: si2 = sj2 = s2. (124) С учетом последнего ограничения, формула (123) упрощается: sZ2 ≈ s2 Откуда, окончательно, получаем выражение для искомой постоянной дисперсии аргументов: s2 ≈ Аналогично решается подобная задача для случая линейной функции (112): s2= Принцип равных влияний. Этот принцип используется в случае физически неоднородных аргументов и довольно условен. Под «влиянием» отдельного аргумента понимается произведение квадрата его частной производной на дисперсию этого аргумента, а сам принцип равных влияний заключается в приравнивании таких произведений друг другу: (∂f/∂xi)2si2 = (∂f/∂xj)2sj2 (126) Данное условие приводит к тому, что в формуле (123) оператор суммы å заменяется множителем, равным числу аргументов «n» :
Из формулы (127) получаем n значений искомых дисперсий:
Для линейной функции (112) формула (128) принимает вид:
Принцип имеющихся возможностей. Этот принцип предполагает, что имеется возможность нахождения значений части случайных аргументов Xj с дисперсиями
Имея возможность вычислить первую сумму
находим вторую:
Далее мы можем столкнуться с двумя ситуациями: а) В первом случае решения не существует, так как имеющиеся возможности Во втором случае решение находят, используя уже описанный выше принцип равных дисперсий (125) или принцип равных влияний (128).
Поиск по сайту: |
 (в геодезии это величины, модуль которых порядка X ∙(10-3 - 10-4) и меньше) степень такого приближения вполне удовлетворительна.
(в геодезии это величины, модуль которых порядка X ∙(10-3 - 10-4) и меньше) степень такого приближения вполне удовлетворительна. – ?
– ? :
: ,… , E(Xn) +
,… , E(Xn) +  ).
). + … +(∂f/∂xn) ∙
+ … +(∂f/∂xn) ∙ 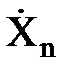 . (119)
. (119) ) =(μ1)iº 0.
) =(μ1)iº 0. =
= 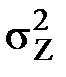 ,
, ≈
≈  *
*  +2
+2 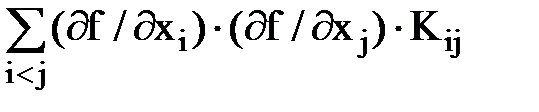 . # (122)
. # (122) ≈
≈ 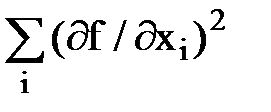 ∙
∙  . (123)
. (123) .
. /
/  . (125)
. (125)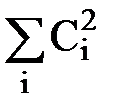 .
. . (127)
. (127) . (128)
. (128)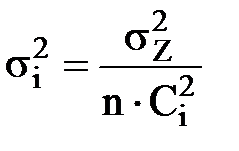 .
.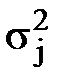 , определяемая, например, парком измерительных приборов. Не теряя общности, мы можем положить, что это – «k» первых аргументов. Дисперсии
, определяемая, например, парком измерительных приборов. Не теряя общности, мы можем положить, что это – «k» первых аргументов. Дисперсии  остальных (n – k) аргументов Xi необходимо найти. Сказанное позволяет разбить сумму (123) на две составляющие:
остальных (n – k) аргументов Xi необходимо найти. Сказанное позволяет разбить сумму (123) на две составляющие: =
=  +
+  =
= 
 +
+ 
 . (129)
. (129) =
= 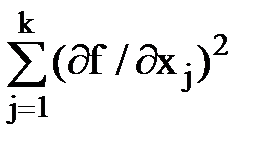
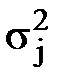 ,
, =
= 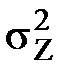 –
– 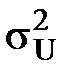 . (130)
. (130)
 0 и б)
0 и б) > 0.
> 0. определения величин Xj приводят к превышению заданного предельного значения дисперсии функции
определения величин Xj приводят к превышению заданного предельного значения дисперсии функции  . Выхода здесь два: либо изменить проект определения величины Z, моделируемый функцией (118), либо искать новые возможности (приборы, технологии), характеризующиеся меньшими дисперсиями
. Выхода здесь два: либо изменить проект определения величины Z, моделируемый функцией (118), либо искать новые возможности (приборы, технологии), характеризующиеся меньшими дисперсиями  .
.