 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Дисперсия линейной функции случайного вектора
Две только что доказанные теоремы позволяют вычислять математическое ожидание суммы или произведения случайных величин, входящих в систему, по математическим ожиданиям слагаемых или сомножителей (с учетом ковариаций стохастически связанных сомножителей), не прибегая к промежуточной операции построения закона распределения результирующей случайной величины. Третья теорема этой группы даст возможность аналогично решить задачу нахождения дисперсии линейной функции случайного вектора по коэффициентам этой функции и по ковариационной матрице вектора её случайных аргументов. Дано: Z= C0 + C1X1 + C2X2 +…+ CnXn = C0 + = C0 + C1n∙Xn1 – линейная функция случайного вектора Xn1; (112) KX = {Kij} – ковариационная матрица этого вектора, элементы которой Kij определяются формулой (100). Найти: D(Z) = Решение: По определению дисперсии (51)
Центрированное значение линейной функции Ż требуется лишь в качестве промежуточной величины, необходимой для вывода, т.к. математические ожидания случайных аргументов E(Xi) не указаны среди известных величин, хотя они и будут участвовать в преобразованиях: Ż= Z – E(Z) = = Возведем эту величину в квадрат, как этого требует формула (113): Ż2= Теперь определим МО этой суммы:
Величины
Для попарно некоррелированных компонентов формула (115) упрощается:
Теорема (116) имеет следствие: дисперсия алгебраической суммы попарно некоррелированных случайных величин равна сумме дисперсий этих случайных величин:
Задача 2.14 [8]. Определить границы, в которых находится абсолютное значение коэффициента корреляции rXY. Дано: X и Y– две коррелированные случайные величины; их коэффициент корреляции rXY = KXY / (sX∙sY). Найти: |ρXY| – ? Решение: Составим линейную функцию Zкоррелированных случайных аргументов X и Y: Z = sY ∙X Найдем её дисперсию по формуле (115):
Поскольку дисперсия любой случайной величины по определению положительна, то справедливо неравенство: 2 Разделив его на первое слагаемое левой части, увидим что 1 ± ρXY > 0, откуда получим искомые границы: | ρXY| ≤ 1. Итак,абсолютное значение коэффициента корреляции не превышает единицы. #
Поиск по сайту: |
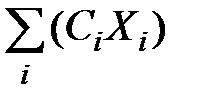 =
=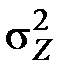 – ?
– ?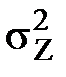 =
= 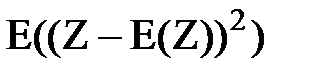 =
= 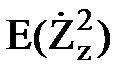 . (113)
. (113)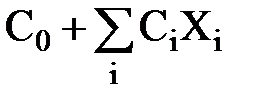 -
- 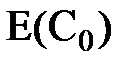 -
- 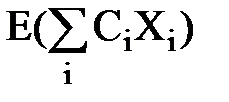 =
=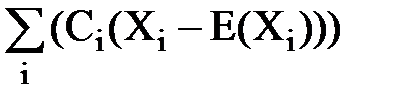 =
= 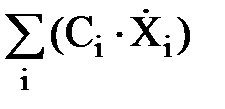 .
. =
=  .
.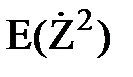 =
= 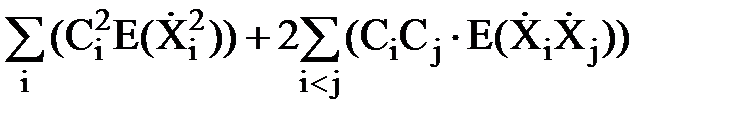 . (114)
. (114)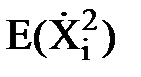 и
и 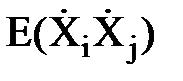 представляют собой дисперсии
представляют собой дисперсии 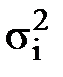 и ковариации Kij, соответственно, i-ых и j-ых компонентов случайного вектора и являются диагональными и недиагональными элементами ковариационной матрицы KX, которая полагается известной. Окончательно имеем:
и ковариации Kij, соответственно, i-ых и j-ых компонентов случайного вектора и являются диагональными и недиагональными элементами ковариационной матрицы KX, которая полагается известной. Окончательно имеем: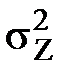 =
= 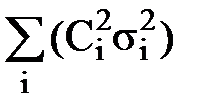 + 2
+ 2 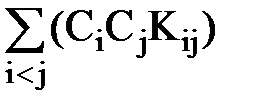 . # (115)
. # (115)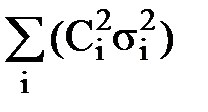 . (116)
. (116)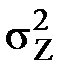 =
= 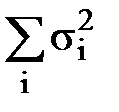 . (117)
. (117)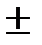 sX ∙Y.
sX ∙Y.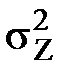 =
= 
 +
+ 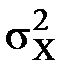
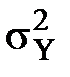
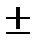 2
2 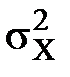
 ρXY.
ρXY.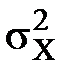

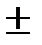 2
2 
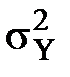 ρXY> 0.
ρXY> 0.