 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Применение динамического программирования для выбора графика сработки водохранилища для ГЭС ⇐ ПредыдущаяСтр 5 из 5
Рассмотрим систему, в которой ГЭС работает на нагрузку параллельно с обобщенной ТЭС.
Нагрузка ГЭС однозначно определяется расходом воды из водохранилища, что приводит к изменению уровня ГВБ. Поэтому в качестве оптимизируемой переменной принимаем отметку ГВБ – x(t). Полагаем, что известен цикл t = 24 часа, известна отметка в начале и в конце цикла регулирования x0 и xК. Известен также прогнозируемый суточный график нагрузки PH(t) (рис.1.38), зависимость объема воды в водохранилище от уровня V(x) (рис. 1.39):
Задаются также зависимость отметки ГНБ от расхода воды Q (рис.1.40) и расходная характеристика ТЭС (рис.1.41):
Нагрузка ГЭС определяется прогнозом приточности, называемым гидрографом QПР(t) (рис.1.42).
Как известно, процесс оптимизации разбивается на шаги по времени. Основное уравнение динамического программирования при развитии условной оптимизации с начального состояния
где S– состояние в конце i-го шага, Ui – управление на i-м шаге, Wi(S) – условно оптимальная эффективность на всех шагах до i-го, при условии, что система находится в состоянии S. Ui(S) – условно оптимальное управление на i-м шаге, совместно с U1,..,Ui-1 формирующее вектор оптимального управления. Cвойства системы определяют характер зависимости эффекта на шаге wi(S,Ui) и состояния в начале шага S’=f(S,Ui) как функции только S и управления Ui.
В конце 1-го шага намечается несколько возможных состояний отметки ГВБ, и для каждого определяется расход топлива на ТЭС расчетом по следующему алгоритму: 1) При x0 и xi находим V(x0) и V(xi); 2) Считается средний расход воды 3) По расходу находим отметку xГНБ; 4) Определяем средний напор: 5) Находим мощность 6) Определяем нагрузку ТЭС На втором шаге в конце его аналогично намечаются возможные состояния, и для каждого состояния рассматривается все переходы из возможных состояний в конце первого. Для каждого перехода по отметкам в начале и в конце по рассмотренному алгоритму считаются расходы на шаге. Условно оптимальное управление на шаге выбирается по минимуму расхода на 1-ом и 2-ом шагах, определяющего условно оптимальную эффективность для рассмотренного состояния.. Это условно-оптимальное управление запоминается. Такая условная оптимизация проводится последовательно для всех этапов, включая и последний. Оптимальный график находится обратным ходом от xК к x0., используя запомненные условно оптимальные управления. Недостаток метода – большой объем вычислений.
Поиск по сайту: |


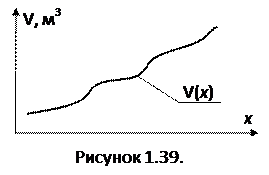



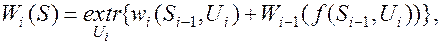
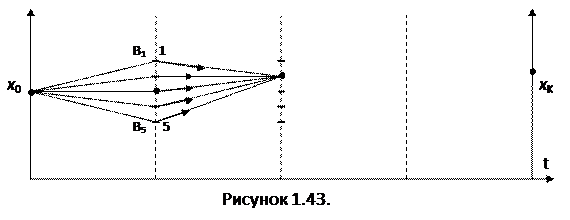
 ;
; ;
;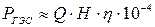 ;
; и расход топлива.
и расход топлива.