 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Формулировка задачи оптимизацииСтр 1 из 5Следующая ⇒
Задачи оптимизации режима. Критерии. Оптимизация режимов энергосистем Режимом энергосистемы называют некоторое состояние ее, определяемое значениями температуры – t°,давления – p, частоты – f, напряжения – U, тока –I, активной мощности – P, реактивной мощности –Q и других физических величин, называемых параметрами режима, которые характеризуют процесс производства, преобразования, передачи и распределения энергии. Режимы делятся на стационарные и переходные. Оптимизируются только стационарные режимы. Оптимизация обеспечивается на всех этапах: 1. Оптимально должно работать все оборудование (с максимальным КПД). Это определяется в основном его техническим состоянием; 2. Распределение нагрузки между параллельно работающими агрегатами; 3. Распределение нагрузки между объектами ЭС. Здесь экономический эффект достигается не только за счет экономии топлива в процессе генерации, но и за счет снижения потерь в сети. Параметры режима ЭС Математическая модель режима – это система нелинейных алгебраических уравнений, как правило, узловых.
где
n – количество независимых узлов. Для решения системы должны задаваться независимые параметры, к числу которых относятся узловые мощности и напряжения в балансирующем узле. Имея эти параметры можно однозначно определить режим (если он существует) путем решения системы (1). Все остальные параметры режима, получаемые на основе расчета: напряжения в узлах ЭС – US, потоки по линиям –Pl, Ql, токи в ветвях –Il,потери – DP и др., называют зависимыми параметрами режима. Часть независимых параметров (узловые мощности) в нормальных условиях не подчиняются диспетчеру (нагрузки в узлах). Остальные (мощности источников) должны оптимизироваться. К числу независимых параметров относятся и коэффициенты трансформации автотрансформаторов связи сетей разных напряжений (КТ), которые могут регулироваться с помощью РПН. Своеобразным независимым параметром является и состав включенного в работу оборудования, который характеризуется графом G. Независимые параметры режима, оптимизация которых должна проводиться при диспетчерском управлении, можно рассматривать как вектор X = { Pi, Qi, KT, G, }, где индекс i определяет источники. По аналогии вектор зависимых параметров объединяет все остальные параметры режима, однозначно определяемые при фиксированных допустимых значениях всех независимых параметров: Y = {US, Pl, Ql, Il, d, DP,… } Для определения Y при заданных Xиспользуются различные методы и программы расчета стационарных режимов. Формулировка задачи оптимизации В общем случае оптимизация заключается в поиске такого состава оборудования и параметров его работы, при которых потребности в энергии за период T обеспечиваются при минимальных затратах. Решение этой сложной задачи обычно проводится в два этапа. На первом выбирается состав включенного в работу оборудования при упрощенной оптимизации режима. На втором этапе для принятого состава оборудования .проводится оптимизация режима его работы. При этом должны учитываться затраты не только в энергосистеме, но и у потребителей. В состав затрат в энергосистеме входят амортизация, зарплата, стоимость топлива и различные налоговые отчисления. От режима в основном зависит расход топлива, который и является определяющим целевую функцию. У потребителей затраты возникают из-за низкого качества электроэнергии, определяемого в первую очередь уровнем напряжения на их шинах. Наличие на потребительских подстанциях трансформаторов с РПН позволяет поддерживать оптимальное напряжение в пределах регулировочного диапазона. В связи с этим затраты у потребителей можно в общем случае не учитывать. Таким образом, в качестве целевой функции можно принять:
где
T – расчетный период. Оптимизацию за период T проводят там, где имеются в системе электростанции с ограниченным запасом первичного ресурса топлива на ТЭС или воды на ГЭС При нормированных запасах топлива можно проводить оптимизацию для каждой ступени графика отдельно и независимо
Оптимизация должна проводиться с учетом ограничений, накладываемых на независимые параметры, например на мощности электростанций Расходная характеристика топлива F(Х) ® min , G(x) >= 0. ЗдесьХ = {x1,…,xn} – вектор неизвестных, G(X) = {g1(x),…,gm(x)} – вектор-функция, состоящая из m элементов. Если F(Х) или g(Х) или оба нелинейные, то задача относится к нелинейному программированию.
Поиск по сайту: |

 - матрица узловых проводимостей, имеет порядок n;
- матрица узловых проводимостей, имеет порядок n;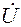 - вектор напряжений в узлах;
- вектор напряжений в узлах; - вектор узловых мощностей;
- вектор узловых мощностей;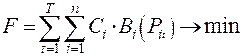
 - расходная характеристика топлива i-ой ТЭС;
- расходная характеристика топлива i-ой ТЭС; - цена топлива;
- цена топлива;
 , а также на зависимые параметры режима, например на напряжения в узлах
, а также на зависимые параметры режима, например на напряжения в узлах  .
. является нелинейной зависимостью. Ограничения на зависимые параметры также являются нелинейными, поэтому задача оптимизации относится к нелинейному программированию, которая в общем виде записывается так:
является нелинейной зависимостью. Ограничения на зависимые параметры также являются нелинейными, поэтому задача оптимизации относится к нелинейному программированию, которая в общем виде записывается так: