|
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Расчет высоты абсорбера по числу единиц переноса
Высота насадки определяется как произведение числа единиц переноса
Множитель
Множитель
Число единиц переноса можно определить по формуле , которая применяется в том случае, когда линия равновесия является прямой или близка к ней, а также графическим методом или методом графического интегрирования.
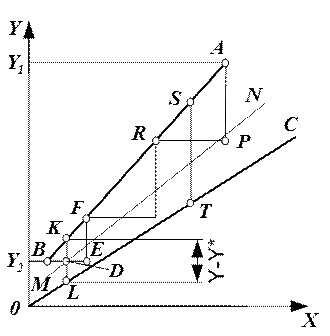
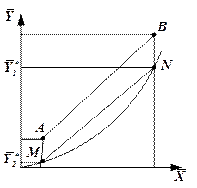
Рассмотрим графический метод. На диаграмме Y – X (рис. 1.6) проводят линию МN, делящую пополам отрезки ординат, заключенные между рабочей линией АВ и линией равновесия ОС. Эти отрезки ординат равны Y – Y* и выражают движущую силу процесса. Затем -через точку В на рабочей линии, соответствующую состоянию фазы G на выходе из аппарата, проводят горизонталь. Эту горизонталь, пересекающуюся с линией МN в точке D, продолжают до точки Е, причем отрезок ВЕ равен удвоенному отрезку ВD. Из точки Е проводят вертикаль ЕF до пересечения с рабочей линией. Из подобия треугольников ВЕF и ВDК следует
Ступенька ВЕF соответствует некоторому участку аппарата, в котором изменение рабочих концентраций в фазе G равно ЕF, а в фазе L соответствует ВЕ. Отрезок КL изображает среднюю движущую силу на этом участке. Так как изменение рабочей концентрации ЕF по построению равно средней движущей силе КL, то ступенька ВЕF соответствует одной единице переноса. Продолжая вписывать указанным выше способом ступеньки до точки А, соответствующей состоянию системы на входе в аппарат, находим число единиц переноса (равное числу ступенек), необходимое для достижения заданного изменения рабочих концентраций между точками А и В. Если между точками В и A не вписывается целое число ступенек, то число единиц переноса, соответствующее последней неполной ступеньке, равно отношению отрезка АP, ограничивающего неполную ступеньку, к вертикальному отрезку SТ между рабочей линией и линией равновесия, проведенного через середину основания неполной ступеньки. Если рабочая линия расположена ниже линии равновесия (то есть при десорбции), то построение ступенек ведут не слева направо, как описано выше, а справа налево, начиная от точки А. Рассмотренный метод применим, если на участке соответствующем одной ступеньке (рис. 1.6) линия равновесия сильно не отличается от прямой. В противном случае отрезок КL не будет изображать среднюю движущую силу на данном участке. В этом случае пользуются более точным методом графического интегрирования [4]. Определение высоты абсорбера через высоту, эквивалентную теоретической тарелке. Высота слоя насадки Нн рассчитывается по уравнению
где Число теоретических тарелок-ступеней изменения концентрации в абсорбере определяют обычно графическим путем (см. рис. 1.3). Высоту насадки h, эквивалентную одной теоретической тарелке, для условий, соответствующих точке нагрузки (началу эмульгирования), определяют по уравнению
Здесь m - среднее значение тангенса угла наклона кривой равновесия к оси абсцисс в координатах
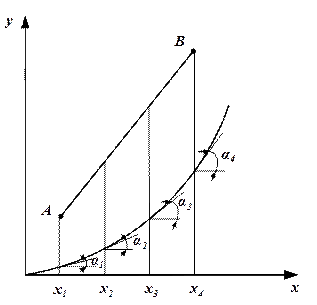
Величину m с достаточной точностью можно найти спрямлением участков кривой равновесия (заменой кривой равновесия ломаной линией), при этом
где i – число прямолинейных участков ломаной линии. Средний наклон линии равновесия можно определить как наклон хорды, проведенной через точки М и N (см.рис. 1.7) ограничивающие рабочий участок линии равновесия: где Если растворимость абсорбируемого газа подчиняется закону Генри и линия равновесия представляет собой прямую, то множитель Эта формула рекомендуется В. В. Кафаровым для колонн, работающих в эмульгационном режиме. Высота насадки, эквивалентная одной единице переноса, зависит от характеристик насадки и фазового состояния газожидкостной системы:
Высота насадки, эквивалентная одной единице переноса для газовой фазы, hy определяется следующим образом: для нерегулярных насадок
для регулярных насадок
Величина hy может быть также определена по формуле
Высота насадки, эквивалентная одной единице переноса для жидкой фазы hy, определяется по формуле Эквивалентный диаметр насадки: Критерий Рейнольдса:
Массовые скорости:
Диффузионный критерий Прандтля:
Приведенная толщина пленки жидкости, стекающей по насадке:
Тарельчатые колонны. Определение высоты тарельчатой колонны проводится по уравнению
где Определение числа тарелок. Определение числа тарелок может быть выполнено несколькими методами. Первый и наиболее простой из них использует так называемый средний к.п.д. тарелок. Из-за недостаточной теоретической обоснованности его применяют при приближенных расчетах. По этому методу число тарелок п определяют по формуле:
Здесь Значения η определяют по опытным данным и находятся в пределах 0,3 - 0,8. По другому методу действительное число тарелок определяется также графическим методом с построением кинетической кривой. Для построения кинетической кривой предложено несколько способов. Первый способ построения кинетической кривой основан на общих положений массопередачи. В соответствии с ним после построения рабочей линии и кривой равновесия рассчитывается коэффициент массопередачи:
где Коэффициент массоотдачи в газовой и жидкой фазах: для колпачковых тарелок
для ситчатых тарелок
где Число единиц переноса одной тарелки:
Здесь
Определяем величину Су:
Величина отрезков на вертикалях диаграммы у – х между линией рабочих концентраций и вспомогательной кинетической кривой
На линии рабочих концентраций (рис. 1.8) наносят ряд точек А1, А2, А3 и т. д., а на линии равновесия – соответствующие им точки С1, С2, С3 и т. д. Пользуясь полученным равенством , находят на отрезках Число единиц переноса n на одну тарелку может быть определено в зависимости от чисел переноса для газовой фазы n1 и для жидкой фазы n2 по уравнению Значения nг и nж для колпачковых и ситчатых тарелок приведены в [4]. После определения n0 находим относительный коэффициент извлечения Е:
где Относительный коэффициент извлечения Е представляет собой отношение количества поглощенного на тарелке компонента к количеству, поглощенному при достижении равновесия между газом и находящейся на тарелке жидкостью.
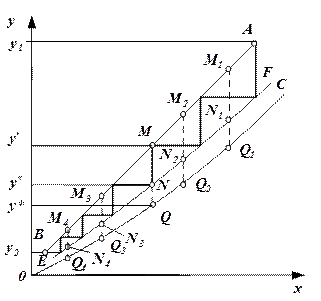
Исходя из изложенного, число тарелок можно найти графически следующим путем. Определив Е из формулы , проводят на у – х диаграмме рис. 1.9 ряд вертикальных прямых
Кинетическую кривую можно построить также следующим образом. Задаемся рядом значений х, на оси абсцисс проводим из этих точек вертикальные линии, пересекающие линию равновесия и рабочую линию (рис. 8.10). В точках пересечения с равновесной кривой проводим касательную к линии равновесия. Определяем тангенс угла наклона касательной линии m. Для каждого значения m определяем величину n0 и Е. В соответствии с полученными значениями Е строим кинетическую кривую.
Поиск по сайту: |
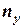 на высоту насадки hу, эквивалентную одной единице переноса:
на высоту насадки hу, эквивалентную одной единице переноса: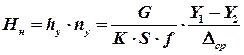 .
.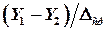 называется числом единиц переноса. Величина
называется числом единиц переноса. Величина 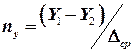 .
. представляет собой высоту участка насадки, соответствующего одной единице переноса, то есть изменению концентрации улавливаемого компонента в газе Y на величину Dср и называется высотой единицы переноса:
представляет собой высоту участка насадки, соответствующего одной единице переноса, то есть изменению концентрации улавливаемого компонента в газе Y на величину Dср и называется высотой единицы переноса: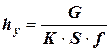 .
.
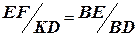 . Но по построению
. Но по построению 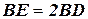 и
и 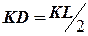 . Таким образом,
. Таким образом,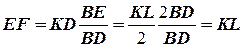 .
.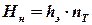 ,
,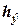 - высота, эквивалентная теоретической тарелке;
- высота, эквивалентная теоретической тарелке; 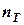 - число теоретических тарелок.
- число теоретических тарелок.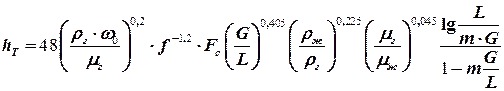 .
. .
.
 ,
,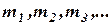 – тангенсы углов наклона прямых на отдельных участках,
– тангенсы углов наклона прямых на отдельных участках,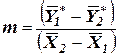 ,
,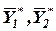 – ординаты точек М и N, а
– ординаты точек М и N, а 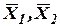 – абсциссы этих точек.
– абсциссы этих точек.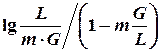 из формулы принимается равным единице. Высота насадки, эквивалентная одной теоретической ступени, hэ может быть рассчитана по уравнению
из формулы принимается равным единице. Высота насадки, эквивалентная одной теоретической ступени, hэ может быть рассчитана по уравнению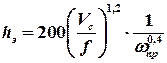
 .
.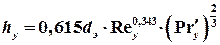 ;
;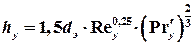 .
.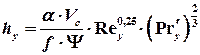 .
.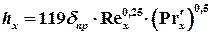 .
.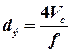 .
.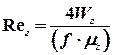 ,
, 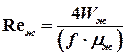 .
.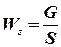 ;
; 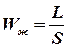 .
. ;
; 
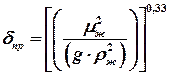 .
.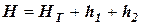 ,
,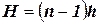 – высота тарельчатой части колонны, м;
– высота тарельчатой части колонны, м;  – высота сепарационной части колонны, м;
– высота сепарационной части колонны, м;  – расстояние от нижней тарелки до днища, м;
– расстояние от нижней тарелки до днища, м; 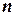 – число тарелок;
– число тарелок; 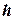 – расстояние между тарелками, м.
– расстояние между тарелками, м. .
. ,
,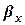 ,
, 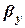 – коэффициент массоотдачи соответственно в жидкой и газовой фазах,
– коэффициент массоотдачи соответственно в жидкой и газовой фазах, 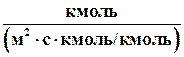 .
. ;
;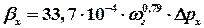 ;
;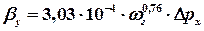 ;
;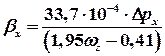 ,
,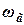 - скорость газа, отнесенная к свободному сечению колонны, м/с;
- скорость газа, отнесенная к свободному сечению колонны, м/с; 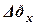 - гидравлическое сопротивление жидкости на тарелке, Па.
- гидравлическое сопротивление жидкости на тарелке, Па. .
.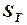 – рабочая площадь тарелки, м2:
– рабочая площадь тарелки, м2: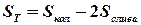 .
.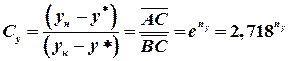 .
.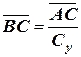 .
.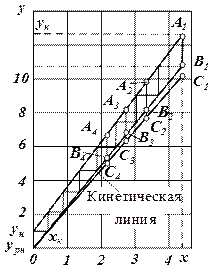
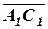 ,и т. д. точки В1,В2,В3и т. д. Проводя через полученные точки В1,В2,В3и т. д. линию, получают вспомогательную кинетическую кривую. Из точки В1 в пределах заданных рабочих концентраций ун и ук между линией рабочих концентраций и вспомогательной кинетической кривой строят ломаную линию А1В1 – А2В2 – А3В3 и т. д. Полученное число ступеней (или отрезков
,и т. д. точки В1,В2,В3и т. д. Проводя через полученные точки В1,В2,В3и т. д. линию, получают вспомогательную кинетическую кривую. Из точки В1 в пределах заданных рабочих концентраций ун и ук между линией рабочих концентраций и вспомогательной кинетической кривой строят ломаную линию А1В1 – А2В2 – А3В3 и т. д. Полученное число ступеней (или отрезков  ) и дает необходимое для заданных условий число тарелок.
) и дает необходимое для заданных условий число тарелок.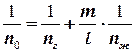 .
.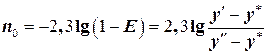 ,
,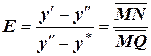 .
.
 ,
, 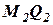 и т. д. и делят эти отрезки между линией равновесия и рабочей линией в отношении
и т. д. и делят эти отрезки между линией равновесия и рабочей линией в отношении 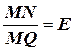 . Через найденные при этом точки N1, N2 и т. д. проводят линию ЕF, называемую кинетической кривой. Далее, начиная от точки А, соответствующей составу газа и жидкости на входе в аппарат, вписывают между рабочей и кинетической кривой ступенчатую линию из вертикальных и горизонтальных участков отрезков, как показано на рис. 1.9. Число вертикальных отрезков этой ступенчатой линии между начальным и конечным составами газа у1 и у2 равно числу тарелок, необходимому для достижения заданного изменения состава газа.
. Через найденные при этом точки N1, N2 и т. д. проводят линию ЕF, называемую кинетической кривой. Далее, начиная от точки А, соответствующей составу газа и жидкости на входе в аппарат, вписывают между рабочей и кинетической кривой ступенчатую линию из вертикальных и горизонтальных участков отрезков, как показано на рис. 1.9. Число вертикальных отрезков этой ступенчатой линии между начальным и конечным составами газа у1 и у2 равно числу тарелок, необходимому для достижения заданного изменения состава газа.