 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
ГАРМОНИЧЕСКИЕ КОЛЕБАНИЯ. КИНЕМАТИКА ГАРМОНИЧЕСКИХ КОЛЕБАНИЙ
КИНЕМАТИКА ГАРМОНИЧЕСКИХ КОЛЕБАНИЙ
Основные понятия, законы и формулы
1.1. Гармонические колебания – колебания, при которых колеблющаяся величина
где 1.2. Циклическая частота связана с периодом где Следует обратить внимание на различие наименований и размерности циклической и линейной частот:
1.3. Скорость колеблющейся точки:
1.4. Ускорение колеблющейся точки:
Скорость и ускорение изменяются по гармоническому закону с амплитудами
1.5. Гармонические колебания можно представить комплексным выражением. С помощью формулы Эйлера:
где
В теории колебаний принимается, что колеблющаяся величина
ДИНАМИКА ГАРМОНИЧЕСКИХ КОЛЕБАНИЙ Основные понятия, законы и формулы 2.1. Сила, действующая на колеблющуюся материальную точку
пропорциональна смещению материальной точки и направлена в противоположную сторону (к положению равновесия). 2.2. Кинетическая энергия колеблющейся материальной точки:
2.3. Потенциальная энергия материальной точки, колеблющейся под действием квазиупругой силы
где 2.4. Полная энергия
На рис. 2. приведены графики зависимости энергий Энергии
ГАРМОНИЧЕСКИЕ ОСЦИЛЛЯТОРЫ
Основные понятия, законы и формулы
3.1. Гармонический осциллятор – система (тело), совершающая гармонические колебания, описываемые уравнением вида:
Примерами гармонических осцилляторов будут пружинный, физический, математический маятники, совершающие свободные колебания без трения под действием квазиупругой силы (или момента силы), т.е. силы, направленной к положению равновесия и зависящей от смещения из этого положения линейно. 3.2. Возьмем начало где Тогда, согласно основному уравнению динамики, уравнение движения маятника примет вид:
или
где Решение этого уравнения:
3.3. Физический маятник – твердое тело, совершающее колебания под действием силы тяжести вокруг неподвижной горизонтальной оси, не проходящей через центр масс С тела, рис. 4. Выберем положительное направление отсчета угла
Уравнение динамики вращательного движения твердого тела примет вид:
или
или
где Решением дифференциального уравнения будет уравнение движения физического маятника:
Физический маятник совершает гармонические колебания с циклической частотой
3.4. Математический маятник – материальная точка массы Математический маятник можно представить как предельный случай физического маятника, вся масса которого сосредоточена в его центре масс, момент инерции маятника (момент инерции материальной точки) Период колебаний и циклическая частота математического маятника соответственно равны
3.5. Приведенная длина физического маятника – это длина такого математического маятника, который колеблется с физическим маятником синхронно. Периоды колебаний физического и математического маятников будут одинаковы. При этом условии приведенная длина физического маятника
Поиск по сайту: |
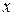 (например, линейное или угловое смещение из положения равновесия) изменяется со временем
(например, линейное или угловое смещение из положения равновесия) изменяется со временем  по закону синуса или косинуса:
по закону синуса или косинуса: или
или  ,
,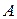 – амплитуда колебаний (максимальное значение колеблющейся величины),
– амплитуда колебаний (максимальное значение колеблющейся величины),  – фаза колебаний в момент времени
– фаза колебаний в момент времени  – начальная фаза в момент времени
– начальная фаза в момент времени  ,
,  – циклическая (круговая) частота колебаний.
– циклическая (круговая) частота колебаний.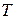 и линейной частотой
и линейной частотой 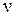 как
как  ,
,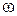 ,
, 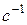 ;
; 

 и
и  соответственно. При этом скорость опережает смещение
соответственно. При этом скорость опережает смещение 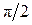 , а ускорение – на
, а ускорение – на  . На рис. 1 приведены графики зависимостей
. На рис. 1 приведены графики зависимостей  ,
,  ,
,  для случая
для случая 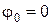 .
.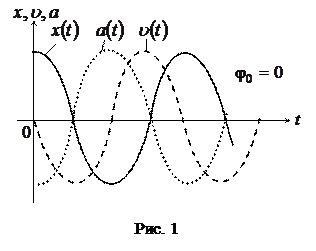
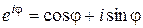 ,
, – мнимая единица, легко видеть тождественность следующих математических выражений:
– мнимая единица, легко видеть тождественность следующих математических выражений: .
. вещественной части принято опускать):
вещественной части принято опускать): .
. ,
, .
. :
:
 – коэффициент упругости
– коэффициент упругости  .
. .
. ,
,  от времени. Из рисунка видно, что в процессе колебаний происходит переход потенциальной энергии в кинетическую и обратно.
от времени. Из рисунка видно, что в процессе колебаний происходит переход потенциальной энергии в кинетическую и обратно. и
и  , т.е. с частотой, которая в 2 раза превышает частоту изменения смещения
, т.е. с частотой, которая в 2 раза превышает частоту изменения смещения 
 .
. Пружинный маятник – грузик массой
Пружинный маятник – грузик массой  на пружине жесткостью
на пружине жесткостью  оси
оси  ,
, – растяжение пружины.
– растяжение пружины.
 ,
, 
 – ускорение;
– ускорение;  .
. Пружинный маятник совершает гармонические колебания с циклической частотой и периодом:
Пружинный маятник совершает гармонические колебания с циклической частотой и периодом: ;
;  .
. против часовой стрелки (ось
против часовой стрелки (ось  проходит через точку О и направлена к нам). Тогда проекция момента силы тяжести на ось
проходит через точку О и направлена к нам). Тогда проекция момента силы тяжести на ось  .
. ,
, ,
, ,
, – угловое ускорение маятника относительно оси
– угловое ускорение маятника относительно оси 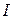 – момент инерции маятника относительно оси
– момент инерции маятника относительно оси  – расстояние между точкой подвеса и центром масс маятника;
– расстояние между точкой подвеса и центром масс маятника;  соответствует малым колебаниям маятника, т.е. малым отклонениям маятника из положения равновесия.
соответствует малым колебаниям маятника, т.е. малым отклонениям маятника из положения равновесия. .
. ;
;  .
. , и совершающая колебания в вертикальной плоскости под действием силы тяжести.
, и совершающая колебания в вертикальной плоскости под действием силы тяжести. , где расстояние от оси до центра масс равно длине маятника
, где расстояние от оси до центра масс равно длине маятника  .
. и
и 
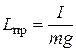 .
.