 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
В соответствии с уравнением Дюпюи ⇐ ПредыдущаяСтр 4 из 4
Отделим переменные и проинтегрируем от сечения 1 до сечения М:
а на всем протяжении отсечения 1 до сечения 2:
тогда Для конечного сечения (на урезе правой реки), где x=L1-2
Определение расстояния до водораздела. Наличие инфильтрации приводит к возникновению на поверхности грунтовых вод подземного водораздела. При этом движение подземных вод от водораздела в сторону рек отличается. Расход через сечение на водоразделе равен нулю (qx = 0). Обозначив расстояние до водораздела через а, и учитывая, что qx = 0, найдем а:
Если h1 = h2, то а= если h1 > h2, то а< если h1 < h2 , то а> Значение а может быть отрицательным (а<0) или больше L1-2, когда водораздел находится за пределами междуречного массива. Построение кривой депрессии. Используя уравнение
определим ординату кривой депрессии на расстоянии x от левой реки Для нахождения q1 необходимо решить другое уравнение относительно hx,
отсюда с учетом q1 откуда: Это уравнение эллипса. Следовательно, в междуречном массиве кривая депрессии грунтовых вод при наличии инфильтрационного питания описывается уравнением эллипса, при отсутствии инфильтрационного питания - уравнением параболы Максимальная мощность ординаты кривой депрессии находится на водоразделе и поэтому, приняв х = а в предыдущем уравнении можно получить hmax
Расчет расходов и ординат депрессии междуречных потоков грунтовых вод с наклонным залеганием водоупора сложный и еще недостаточно разработанный, поэтому на практике обычно водоупорное основание условно считают горизонтальным. Потоки подземных вод в междуречном массиве неоднородного строения. Положим W=const и горизонтальное залегание водоупора i =0. Пусть в пределах междуречья имеются 2-а участка: L1, где k1 и L2 , где k2 Составим уравнение для единичного расхода на границе 2-ух фрагментов используя формулу:
для фрагмента 1-S
для фрагмента S-2
В силу неразрывности потока приток подземных вод к правой границе левого фрагмента равен их оттоку от левой границы правого фрагмента, поэтому правые части этих формул можно приравнять:
откуда
Задание Задача 1.(Для варианта 1). Междуречье шириной 9км сложено трещиноватыми известняками, которые подстилаются плотными горизонтально залегающими глинами. Мощность водонасыщенных известняков у рек 83м и 75м. Коэффициент фильтрации 26м/сут. В инфильтрационном питании участвуют лишь 30% годового количества осадков, которое достигает 380мм. Необходимо определить единичный расход подземных вод в реке и построить депрессионную кривую. Таблица 1.Исходные данные по вариантам для задачи 1.
Задача 2.(Для варианта 1). Расстояние от реки до канала равно 1730м. На этом расстоянии водоносные аллювиальные пески с коэффициентом фильтрации 10.0м/сут. Среднее годовое количество осадков характеризуется величиной 520мм. В инфильтрационном питании участвует только 31% этих осадков. Уровни воды в реке и канале находятся на отметках соответственно 34.0м и 33.0м. Водоупорное ложе плотных глин залегает наклонно с отметками 20.0м у реки и 24.0м у канала. Определить величины единичного расхода подземного стока в реку и канал, расстояние до водораздела, ординату водораздела, а также построить депрессионную кривую. Таблица 2.Исходные данные по вариантам для задачи 2.
Поиск по сайту: |
 , тогда
, тогда  (2)
(2) , получим для единичного расхода:
, получим для единичного расхода: (3)
(3) , (4)
, (4) (5)
(5) (6)
(6) (7)
(7)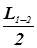 , т.е. водораздел посредине,
, т.е. водораздел посредине, (9)
(9)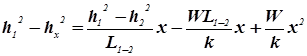 (10)
(10)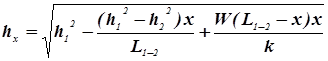 (11)
(11) (12)
(12) (14)
(14)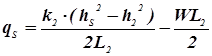 (15)
(15)
 (16)
(16) (17)
(17)