 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Движение подземных вод в неоднородных водоносных пластах
Под неоднородными водоносными толщами понимают неоднородные водоносные пласты сложенные различными по литологическому составу (по водопроводности) породами в горизонтальном и вертикальном направлении. Неоднородные водоносные пласты в природе встречаются чаще, чем однородные. Особенно характерна неоднородность для аллювиальных отложений речных долин (нижняя часть крупнозернистые пески, а в верхней - мелкозернистые - суглинки, торфы). Наряду с изменением фильтрационных свойств изменяется и мощность водоносного горизонта. Наибольшее распространение получили три типа неоднородности? 1) слоистая неоднородность (чередующиеся пласты водоносных пород); 2) двухслойные пласты (вертикальная неоднородность) - верхний слой имеет меньшуюнеоднородность или наоборот); 3)горизонтальная неоднородность. Если фильтрационные свойства отличаются не более чем в 5-10 раз, то условно считают область однородной (осредняется коэффициент фильтрации). Если отличаются более, то такие пласты уже считают неоднородными. Неоднородность определяется путем расчета К в разных направлениях,
Рис.1 Вертикальная неоднородность водоносных пластов (движение подземных вод параллельно напластыванию) Единичный расход всего потока в слоистом пласте можно записать Q=q1+ q2+ q3+…+ qn (1) q=(k1h1+k2h2+…+knhn)I (2) но: q = kсрhI (3) где kср - средний коэффициент всего водоносного пласта, h - суммарная мощность всех слоев = (h1+ h2+…+hn). тогда (k1h1+k2h2+…+knhn)I = kсрhI (4) получаем формулу определения среднего значения коэффициента фильтрации для слоистого пласта:
Его называют средневзвешенным по мощности или средним, приведенным или эквивалентным. Он является показателем водопроводности всего комплекса неоднородной толщи
Формула применима как к безнапорному, так и напорному потокам. Для напорного вместо h1, h2,… hn пишется m1, m2…mn При равномерном движении депрессионная кривая будет представлять собой прямую линию. 2. Движение подземных вод нормально к напластованию.
Рис.2 Вертикальная неоднородность водоносных пластов (движение подземных вод перпендикулярно напластыванию) k - коэффициент фильтрации каждого слоя; I - напорные градиенты; ΔH - падение напора в каждом слое.
Сравнивая kср для горизонтального и вертикального движения, можно убедиться, что первое значение будет максимальным (kсргор.-max), а второе минимальным (kсрверт.-min).
3. Движение подземных вод в двухслойном пласте. Рассмотрим случай, когда водоносный пласт состоит из двух горизонтально залегающих слоев имеющих различную водопроводимость: h – мощность грунтового потока, m – мощность напорного потока.
Рис.3 Движение подземных вод в двухслойном пласте. Расход всего потока в любом сечении можно рассматривать как сумму расходов верхнем и нижнем слоях. Предполагается, что в верхнем слое находится поток со свободной поверхностью, а в нижнем - напорный поток, оба имеют единую пьезометрическую поверхность.
где: q1 - грунтовый поток; q2 - напорный поток.
Разделив переменные и проинтегрировав, получим: но т.к. Это уравнение применимо и для пласта состоящего из трех и более слоев. В этом случае h1, и h2 - мощности верхнего слоя, а m1 - суммарная мощность всех остальных нижележащих слоев. Вместо k1 следует применять средневзвешенный коэффициент верхних слоев. Применяется эта формула при соотношении Движение подземных вод в неоднородном пласте с резкой сменой водопроницаемости в горизонтальном направлении. Такое изменение очень часто имеет место в надпойменной и пойменной террасах речных долин, или на склонах речных долин, имеющих различные коэффициенты фильтрации.
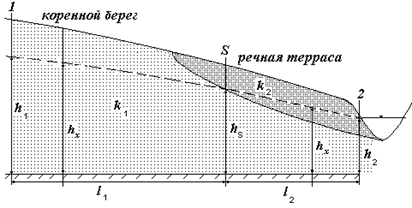
l1 + l2 =L Рис.4 Горизонтальная неоднородность водоносных слоев.
Напишем уравнение единичного расхода потока отдельно для участка коренного берега и речной террасы, 1.для участка I -S:
2.для речной террасы S-2:
Сложив эти два уравнения, и исключив hs , получим:
Решив уравнение относительно q, получим для единичного расхода (формула Каменского):
Приравняв правые части уравнении для участка 1-S и S-2, получим:
Ордината депрессионной кривой hx определяется отдельно для участка коренного берега и речной террасы по формуле:
Построение кривой депрессии в пределах участков 1-S и S-2 выполняется с использованием формул (12) и (13), записанных для любых участков 1-X и X-2: для участка 1-S: отсюда для участка S-2: отсюда Если грунтовый поток проходит по коренному берегу речной долины и нескольким террасам с разной водопроводностью, то формула выглядит так:
Здесь, l1 и k1 - протяженность и коэффициент фильтрации коренного берега. Для напорного потока с резкой сменой водопроводимости в горизонтальном направлении можно получить расчетные формулы, пользуясь известной подстановкой: грунтовый поток напорный поток Данный способ дает возможность переходить от более простых решений напорного потока к более сложным - для грунтового. Для определения расхода потока:
для определения величины напора в промежуточном сечении:
Для нахождения Hx в любом сечении используется формула:
Пьезометрическая кривая строится отдельно для каждого участка (коренной берег и терраса). Подъем уровня в поверхностном водоеме, дренирующем подземный поток, приведет к подпору грунтовых вод. В случае, если при подпоре единичный расход сохраняется неизменным (q=const) , порядок расчета подпора будет следующим: а) в сечении 2 определяется мощность потока h2¢ h2¢ = h2 +DH (27) б)определяется мощность грунтового потока на стыке пород с разным коэффициентом фильтрации hS¢ hS¢= в)в сечении 1 определяется мощность потока h1¢ h1¢= г) по формулам (19) и (21) определяются ординаты кривой депрессии при подпоре, мощности hX1¢ и hX2¢, подставляя в них измененные параметры h1¢ и h2¢ .
Задание. Для варианта 1. Скважина пробурена через надпойменную террасу L в 500м от уреза реки (к1=36м/сут). К берегу реки прислонена аллювиальная терраса l2 шириной120м (к2=15м/сут). При бурении скважины уровень грунтовых вод H1 установился на отметке 111м; залегание водоупора Z – на отметке 106м; горизонт воды в реке H2 – на отметке 109м. Отметка поверхности верхней террасы B1 – 126м, нижней B2– 123м. Уклон водоупорного основания i = 0. Определить единичный расход грунтовых вод, построить кривую депрессии до и после повышения горизонта воды в реке (DH) на 2,6м.
Для остальных вариантов исходные данные этой задачи приведены в таблице 1.
Таблица 1 Исходные данные к задаче для различных вариантов.
Задание №3 Движение подземных вод в междуречном массиве однородного строения, при наличии инфильтрационного питания. Расход потока не меняется, если на пути фильтрации он не теряет и не приобретает воду. Для этого необходимо, чтобы границы, ограничивающие его снизу, сверху и с боков были непроницаемы. Эти условия, как правило, не соблюдаются, и расход потока на пути фильтрации меняет свои значения. Особенно большую роль играет водообмен подземных вод через зону аэрации, а именно, инфильтрация, конденсация и испарение влаги на свободной поверхности грунтовых вод (Рис.1). Интенсивность этого водообмена на единице площади поверхности грунтовых вод за единицу времени называется инфильтрационным питанием. Положим W=const и горизонтальное залегание водоупора i =0. Тогда граничными условиями задачи будут: W= сonst, К= соnst , i = 0. Согласно Каменскому, единичный расход грунтового потока в междуречном массиве при наличии инфильтрационного питания: qx=q1 + Wx (1) где qx - единичный расход на расстоянии х от уреза левой реки; q1- начальный расход в сечении 1 W - интенсивность фильтрации (в ед. времени на единицу площади)
Рис. 1 Линейный поток безнапорных подземных вод с инфильтрационным питанием в междуречном массиве.
Поиск по сайту: |

 (5)
(5) (6)
(6)
 , (7)
, (7) (8)
(8)
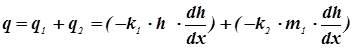 (9)
(9) (10)
(10) , получим:
, получим: (11)
(11) .
.
 , откуда:
, откуда:  (12)
(12) откуда
откуда  (13)
(13) (14)
(14) (15)
(15) (16)
(16) (17)
(17) (18)
(18) (19)
(19) (20)
(20) (21)
(21) (22)
(22) ; получаем :
; получаем :  (23)
(23) (24)
(24) (25)
(25) (26)
(26) (28)
(28) (29)
(29)