 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Для наклонного залегания водоупора
При наклонном водоупоре расход грунтовых вод можно определить по приближенной формуле Г. H. Каменского:
где: H1 и H2 - напоры подземных вод, которые отсчитываются от какой-либо горизонтальной плоскости сравнения, но не от наклонного водоупорного основания. Формула имеет приближенный характер, т.к. при выводе ее, переменная мощность потока h была заменена средней мощностью hср. Для построения депрессионной кривой, из уравнения Каменского, заменим h2 и H2 на hx и Hx .Это возможно из-за постоянства q для любых двух сечений потока.
Для участка потока длиной x уклон можно выразить через уравнение
Если известны величины единичного расхода q, коэффициента фильтрации k и уклон водоупорного ложа i, то при заданном значении x , эти два уравнения представляют собой систему с двумя неизвестными hx и Hx. При ее решении получим:
Если же расход неизвестен, то согласно формуле Каменского будем иметь:
При этом Однако полученные уравнения являются приближенными и справедливы только при постоянных значениях q, k, и i , где уклон имеет не очень большие значения и определяется по уравнению:
Если на исследуемом участке уклон водоупорного ложа заметно меняется, то эти уравнения использовать нельзя. В этом случае необходимо предварительно выделить участки с относительно постоянными уклонами. При радиальных потоках подземных вод, которые часто наблюдаются в излучинах и на прямолинейных участках речных долин, Г.Н.Каменский рекомендует пользоваться следующим уравнением:
где: B1 и В2 –ширина потока в двух его сечениях. Единичный расход потока напорных водпри постоянной мощности водоносного пласта определяется по дифференциальному уравнению:
Для km=const , после интегрирования, получим расчетную формулу:
В условиях пласта переменной мощности напорный поток движется неравномерно, т. е. скорость фильтрации меняется от сечения к сечению. Кривая депрессии при этом приобретает криволинейный характер. При увеличении мощности пласта по направлению движения потока кривая будет иметь вогнутый характер, а при уменьшении – выпуклый.
Рис.2 Схема напорного потока переменной мощности.
Единичный расход напорного потока переменной мощности, по Г.Н.Каменскому, приближенно можно рассчитать по формуле:
Ординаты кривой депрессиинапорных потоков рассчитываются по формулам: для потока с постоянной мощностью: для потока с переменной мощностью:
В.И. Давидович и Н.Н. Биндеман вывели более точную расчетную формулу единичного расхода напорных воддля случая линейного изменения мощности потока. Решение получается на основе интегрирования дифференциального уравнения Дюпюи с учетом переменного значения мощности m , подчиняющейся линейной зависимости. Для обоих случаев изменения мощности, в любом сечении, расположенном на расстоянии x от сечения 1, мощность определяется по формуле:
После интегрирования уравнения: Ординаты кривой депрессиинапорных потоковпо Давидовичу и Биндеману:
Задание. По данным, приведенным в соответствующим варианте табл.1, построить схему и определить общий и единичный расходы плоского грунтового потока в однородном пласте. Таблица 1 Исходные данные для определения q, Q, hx (построения кривой депрессии)
Задание №2
Поиск по сайту: |
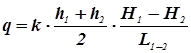 ; (9)
; (9) ; (10)
; (10) (11)
(11) ; (12)
; (12) (13)
(13) (14)
(14)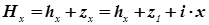 (15)
(15) (16)
(16) ; (17)
; (17) ,где: m –мощность пласта,
,где: m –мощность пласта, 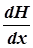 - напорный градиент.
- напорный градиент.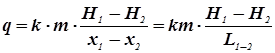 (18)
(18)

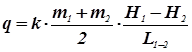 (19)
(19) ; (20)
; (20) (21)
(21)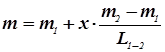 (22)
(22) для напорных вод, получаем расчетную формулу:
для напорных вод, получаем расчетную формулу:  (23)
(23)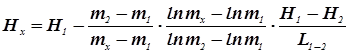 (23)
(23)