 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Кинематика поступательного и вращательного движений
31. Автомобиль трогается с места с постоянным ускорением a1=2 м/с2
32. Два поезда прошли одинаковый путь S за одно и тоже время t, однако один поезд, трогаясь с места, прошел весь путь равноускоренно с ускорением а=3 м/с2, а другой поезд половину пути шел со скоростью υ1=18 км/ч, а другую половину пути – со скоростью υ2=54 км/ч. Найти путь S, пройденным каждым поездом.
33. Тело, движущееся равноускорено с начальной скоростью υ0=1 м/с, пройдя некоторое расстояние, приобретает скорость υ=7 м/с. Какова была скорость тела в тот момент времени, когда оно прошло половину расстояния?
34. За какую секунду от начала движения путь, пройденный телом при равноускоренном движении, втрое больше пути, пройденного за предыдущую секунду, если движение происходит без начальной скорости?
35. Пассажир, стоящий у начала третьего вагона электрички, определил, что начавший двигаться вагон прошел мимо него за t1=5 c, а вся электричка – за t2=15,8 c. Сколько вагонов у электрички? За какое время прошел мимо пассажира последний вагон? Движение электрички считать равноускоренным.
36. Тело, с начальной скоростью υ01=3 м/с и ускорением а1=0,2 м/с2, начинает двигаться из точки А по прямой в точку В, отстающую от А на расстоянии S= 3,46 км. Через время t=20 с из точки В в точку A начинает равноускоренно двигаться второе тело, с начальной скоростью υ02= 2 м/с? Через какое время, после начала движения первого тела, они встретились? Найти ускорение и скорость второго тела в момент встречи.
37. Велосипедист в течение первых пяти секунд двигался из состояния покоя с ускорением а=1 м/с, затем t=0,1 мин двигался равномерно, а последние 25 м равнозамедленно до остановки. Определить время движения велосипедиста и весь пройденный путь.
38. Автомобиль начал движение с ускорением а=0,5 м/с в тот момент, когда мимо него равноускоренно проезжал трамвай со скоростью υ=18 км/ч. Какую скорость будет иметь автомобиль, когда он догонит трамвай? Ускорение трамвая 0,3 м/с.
39. Реактивный самолет летит со скоростью υ=720 км/ч. С некоторого момента самолет движется с ускорением в течение t=10 с и в последнюю секунду проходит 295 м. Определить ускорение и конечную скорость самолета.
40. Два велосипедиста едут навстречу друг другу. Один, имея скорость υ1=18 км/ч, движется равнозамедленно с ускорением а1=20 см/с2, другой, имея скорость υ2=5,4 км/ч, движется равноускоренно с ускорением а2=2 см/с2. Через какое время велосипедисты встретятся и какой путь пройдет каждый из них до встречи? Первоначальное расстояние между велосипедистами 103,25 м.
41. Тормозной путь поезда перед остановкой на станции S=1000м. Определить ускорение и время торможения, если в начале торможения скорость была 40 км/ч. Какова была скорость поезда у светофора, находящегося в средней точке тормозного пути?
42. Мотоциклист и велосипедист одновременно начинают движение из состояния покоя. Ускорение мотоциклиста в 3 раза больше, чем велосипедиста. Во сколько раз большую скорость разовьет мотоциклист: 1) за одно и тоже время; 2) на одном и том же пути?
43. Мальчик скатился на санках с горы длиной 20 м и проехал по горизонтальному участку пути 40 м. Все движение заняло время 15 с. Найти: 1) время торможения; 2) скорость в конце горы; 3) ускорение при торможении.
44. Автомобиль начинает спускаться с горы равноускоренно без начальной скорости и за время t=1 мин, приобретает скорость υ1=27 км/ч. Одновременно навстречу ему начинает равнозамедленно подъем в гору автомобиль, имеющий начальную скорость υ0=20 м/с. За время t=1 мин скорость второго автомобиля уменьшается до υ2=8 м/с. Какое расстояние будет разделять автомобили через t=80 с после начала движения, если длина горы l=2 км?
45. По наклонной доске пустили снизу вверх шарик. На расстоянии S=30 см от начала доски шарик побывал дважды: через 1 с и через 2 с после начала движения. Определить начальную скорость и ускорение шарика, считая его постоянным.
46. За машиной «Жигули», которая ехала со скоростью υ1=54 км/ч, на расстоянии S1= 20м оказался грузовик, движущийся со скоростью υ2= 90км/ч. Какое минимальное ускорение должно быть у «Жигулей», чтобы интервал между машинами оставался не менее S2=5 м? Движение «Жигулей» считать равноускоренным, грузовика - равномерным.
47. Материальная точка перемещается в пространстве так, что вектор ее скорости меняется по закону:
где А=1 м/с2, В=2 м/с3. Найти: 1) модуль скорости в момент времени t=2 с; 2) приращение радиуса – вектора за время от t1=2 с до t2=4 с.
48. Точка перемещается в пространстве так, что ее радиус – вектор меняется с течением времени по закону:
где А=3 м/с2, c=4 м/с4. Найти: 1) путь, пройденный точкой за время от t1=1 с до t2=2 с; 2) модуль мгновенного ускорения в момент времени t=2 с.
49.Ускорение частиц меняется с течением времени по закону:
50. Движение точки по плоскости задано уравнениями:
где А=2 м; В=1 м/с2; С=3 м/с3. Найти: 1) зависимость вектора ускорения точки от времени; 2) путь, пройденный точкой за 10 с от начала движения.
51. Точка движется по окружности радиусом 10см так, что зависимость пути от времени:
52. Точка движется по окружности радиусом R=20см так, что зависимость ее линейной скорости от времени имеет вид:
53. Точка движется по окружности согласно уравнению φ=A + Bt3, где B=1 рад/с3. Найти радиус окружности, если известно, что спустя 5 с от начала движения полное ускорение точки стало равно 400 см/с2.
54. Точка движется по окружности с тангенциальным ускорением, изменяющимся по закону: aτ=Ct, где С=2 см/с3. Через сколько времени от начала движения нормальное ускорение будет в два раза больше тангенциального? Радиус окружности 20 см. 55. Точка движется по окружности радиусом 10 см так, что ее нормальное ускорение меняется по закону: an=At4, где A=4 м/с6. Найти тангенциальное и полное ускорение точки спустя 2с от начала движения.
56. Точка движется по окружности радиусом 4см так, что зависимость пути от времени имеет вид: S=A+Ct3, где А=2 м, С=1 м/с3. Сколько оборотов сделает точка к тому времени, когда ее тангенциальное ускорение станет равным 1,2 м/с2.
57. Точка движется по окружности таким образом, что ее линейная скорость меняется по закону: V=At+Bt3, где А=2 м/c2, В=1 м/c4. Найти путь, который пройдет точка за 5 с от начала движения. Сколько оборотов сделает точка за это время, если радиус окружности 1 м?
58. Точка движется по окружности согласно уравнению y=At + Bt2, где A=2 рад/с, В=1 рад/c2. Найти, сколько оборотов сделает точка спустя 5 с от начала вращения. Чему будет равно ее полное ускорение? Радиус окружности 6 см.
59. Точка движется по окружности радиусом 8 см так, что ее тангенциальное ускорение меняется по закону: aτ=A +Bt, где A=3 м/c2, В=1 м/c3. Найти полное ускорение точки спустя 2 с от начала движения.
60. Точка движется по окружности радиусом 10 см так, что ее нормальное ускорение меняется по закону: an=Bt6, где B=9 м/c8. Найти, какой путь пройдет точка за 20 с от начала движения, чему будет равно ее тангенциальное ускорение в этот момент.
Поиск по сайту: |
 и, достигнув скорости υ=36 км/ч, некоторое время идет равномерно, затем тормозит с постоянным ускорением а2=1 м/с2 до остановки. Определить время движения автомобиля, если он прошел путь S=1 км.
и, достигнув скорости υ=36 км/ч, некоторое время идет равномерно, затем тормозит с постоянным ускорением а2=1 м/с2 до остановки. Определить время движения автомобиля, если он прошел путь S=1 км. ,
, ,
, , где В=2 м/с3; С=1 м/с2. Найти: 1) модуль скорости в момент времени t=2 с; 2) модуль радиуса – вектора в этот момент времени. В начальный момент времени частица покоилась в начале координат.
, где В=2 м/с3; С=1 м/с2. Найти: 1) модуль скорости в момент времени t=2 с; 2) модуль радиуса – вектора в этот момент времени. В начальный момент времени частица покоилась в начале координат.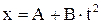 ;
;  ,
, , где A=2 м/с, С=1 м/с3. Найти линейную скорость точки, ее тангенциальное, нормальное и полное ускорение через 2 с от начала движения.
, где A=2 м/с, С=1 м/с3. Найти линейную скорость точки, ее тангенциальное, нормальное и полное ускорение через 2 с от начала движения. , где C=2 м/с2, В=1 м/c3. Найти тангенциальное ускорение точки и путь, пройденный за время 10 с от начала движения.
, где C=2 м/с2, В=1 м/c3. Найти тангенциальное ускорение точки и путь, пройденный за время 10 с от начала движения.