 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Алгоритм Шора (1994) — по заданному целому числу N, найти его простые множители ⇐ ПредыдущаяСтр 5 из 5
В 2001 квантовый компьютер на 7 кубитах с помощью этого алгоритма смог разложить 15 на 3×5. (Наибольшее число, разложенное на квантовом устройстве = 56153 — 2014 год, но не Шором, а адиабатическое вычисление) Алгоритм состоит из двух частей: 1. классическая часть - свести задачу к нахождению периода функции. 2. квантовая часть — найти период. Классическая часть: 1. берём произвольное число a < N. 2. вычисляем НОД(a,N) (наибольший общий делитель). Например, с помощью алгоритма Эвклида — вычитаем из большего числа меньшее. 3. Если НОД(a,N)≠1, то нетривиальный множитель найден, конец. 4. В противном случае, с помощью квантового алгоритма, основанного на дискретном преобразовании Фурье, находим период функции 5. если r нечётное, или a r/2≡ −1 (mod N) - возвращаемся к шагу 1. 6. НОД(ar/2+ 1, N) и НОД(ar/2- 1, N) — нетривиальные множители N. Конец.
Например:
(Примечание: самый быстрый классический алгоритм решения этой задачи — квадратичное решето — основан на той же идее. Но медленнее, т. к. задача поиска порядка функции тяжело решается классическим компьютером)
Квантовая часть: Квантовая цепочка создаётся каждый раз отдельно для каждого N, и каждого случайного выбора a. Находим некоторое Q = 2q,такое что Вход и выход будут содержать суперпозиции состояний от 0 до Q − 1, поэтому состоят из q кубитов. 1. Создаём суперпозицию всех состояний — с помощью вентилей Адамара, или к. преобразования Фурье 2. Конструируем f(x) как к. функцию, и применяем к состоянию выше (Шор использовал алгоритм быстрого возведения в степень, чтобы достичь этого. Это самый долгий шаг. Он заметно сложнее, чем QFT – нужно много вентилей. По сути, он имитирует классический обратимый алгоритм для этой задачи) 3. Применяем к. преобразование Фурье ко входу. (Шор использовал для реализации QFT вентили фазового сдвига и вентили Адамара) (Вентиль Адамара: переводит n кубитов, инициализированных в |0>, в суперпозицию всех 2nортогональных состояний в базисе (|0>,|1>) с равными весами) QFTиспользует Qтый комплексный корень единицы: В результате приходим к состоянию Возьмём x0- наименьший x, что f(x) = z (x0<r), и b — индексирует эти x, пробегая от 0 до (Q- x0-1)/r, так что x0+rb<Q. Тогда получим:
Каждое слагаемое в этой сумме даёт разные пути к одной цели — и возникает к. интерференция: амплитуды состояний, для которых единичные векторы 4. Производим измерение, и получаем y на входе, и z на выходе. Вероятность получить данные y и z тем выше, чем ближе 5. Т.к. yr/Q близко к некоторому целому c, то · s<N · |y/Q - d/s| < 1/2Q. Если d/s не упрощаемая дробь, то s — весьма вероятно наш искомый период r. 6. Проверяем (классически), что
Говоря просто, алгоритм Шора разбивает задачу на Q состояний, каждое из которых — один из возможных r – периодов функции. И затем, благодаря к. спутанности и интерференции, вычисление производится по всем путям одновременно (по сути, это аналог алгоритма к. оценки фазы: вследствие интерференции, амплитуды состояний вдоль перспективных путей стремительно растут, остальные стремительно падают). Отсюда к. выигрыш в скорости. Также алгоритм Шора может использоваться для нахождения дискретного логарифма.
2) Алгоритм Гровера (Leo Grover, 1996) — найти х по заданному у, такой что f(x)=y. Это, по сути, алгоритм инвертирования функции — но он может быть и переформулирован как алгоритм поиска по базе данных (f(x) тогда будет функцией, возвращающей 1 для искомого х, и 0 для всех остальных). В общем виде, f(x) - это чёрный ящик, или оракул, как-то отвечающий на запрос «да» или «нет». Алгоритм Гровера работает за время O(N1/2), где N – размер области определения f(x). Классический алгоритм не может решить этой проблемы за время меньше O(N). И доказано, что O(N1/2) — наименьшее возможное время для любого квантового алгоритма решения, т.е. алгоритм Гровера — оптимальный. На практике, этот алгоритм тоже можно использовать для взлома 128-битного криптографического ключа - методом перебора за 264итераций. Т.е., алгоритм Гровера даёт не экспоненциальное ускорение, по сравнению с классическим (как другие квантовые алгоритмы, применимые в более специфических случаях) — а лишь квадратичное. Но и то неплохо. Алгоритм — вероятностный, т. е. даёт правильный ответ с вероятностью <1. Но предполагается, что количество повторов, чтобы приблизить вероятность к 1 — это постоянная величина, и не зависит от N. Описание:
1. Применяем оператор 2. Применяем оператор Осуществляем измерение, и получаем искомую ω с вероятностью, стремящейся к 1.
Геометрическое объяснение:
Оператор Нам нужно остановиться, когда вектор состояния подойдёт достаточно близко к
На практике, в 2012м, реализовали алгоритм Гровера для четырёх вариантов перебора.
Поиск по сайту: |
 , т. е. такое целое число r, что
, т. е. такое целое число r, что 
 .
.  , где
, где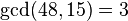 и
и 
 , что означает
, что означает  .
.


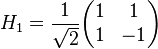
 , чтобы равномерно распределить амплитуду любого данного состояния |x> между всеми Q для состояния |y> - и делать это по-разному для каждого |x>.
, чтобы равномерно распределить амплитуду любого данного состояния |x> между всеми Q для состояния |y> - и делать это по-разному для каждого |x>.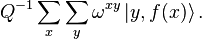 , или если записать иначе:
, или если записать иначе: 

 направлены практически в одну сторону (что значит что вектор
направлены практически в одну сторону (что значит что вектор  направлен вдоль положительной вещественной оси), усиливаются; остальные ослабевают.
направлен вдоль положительной вещественной оси), усиливаются; остальные ослабевают. известное значение y/Q близко к неизвестному c/r. Осуществив (классически) непрерывную дробную последовательность, мы найдём такие аппроксимации d/s, что:
известное значение y/Q близко к неизвестному c/r. Осуществив (классически) непрерывную дробную последовательность, мы найдём такие аппроксимации d/s, что: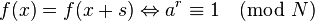 . Если да, то конец. Иначе, пробуем прогнать всю эту часть ещё раз.
. Если да, то конец. Иначе, пробуем прогнать всю эту часть ещё раз. Алгоритм работает на N-мерном пространстве состояний H - для которого надо n=log2 N кубитов. У нас есть унитарный оператор Uω, который зеркально отражает вектор состояния относительно гиперплоскости, перпендикулярной ω.
Алгоритм работает на N-мерном пространстве состояний H - для которого надо n=log2 N кубитов. У нас есть унитарный оператор Uω, который зеркально отражает вектор состояния относительно гиперплоскости, перпендикулярной ω. Мы начинаем с состояния
Мы начинаем с состояния  - равномерной суперпозиции всех возможных состояний величин x:
- равномерной суперпозиции всех возможных состояний величин x: Тогда
Тогда  , Осуществляем «гроверовскую итерацию» r(N) раз (
, Осуществляем «гроверовскую итерацию» r(N) раз (  ):
): .
. .
.
 - кет, перпендикулярный
- кет, перпендикулярный  :
: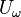 - это, по сути, отражение вектора по отношению к
- это, по сути, отражение вектора по отношению к  ) поворачивает его вектор состояния на угол
) поворачивает его вектор состояния на угол  .
. , где r — это количество гроверовских итераций.
, где r — это количество гроверовских итераций. Смысл GSA состоит в «подскоке амплитуды» (amplitude amplification) целевого состояния за счёт убывания амплитуды всех других состояний.
Смысл GSA состоит в «подскоке амплитуды» (amplitude amplification) целевого состояния за счёт убывания амплитуды всех других состояний.

