 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Относительный сдвиг фазы
Это однокубитный вентиль, определяемый умножением на унитарную матрицу:
Это простейший пример не-классического, квантового вентиля. Он оставляет базовое состояние |0> неизменным, и поворачивает состояние |1> на eiφ. Вероятность измерения |0> или |1> не меняется, но меняется фаза квантового состояния. На сфере Блоха это соответствует повороту в горизонтальной плоскости на угол φ. Вентиль Фредкина (CSWAP) Это универсальный вентиль, переставляющий два последних бита, если первый бит=1.
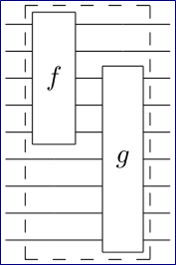
Его свойство — сохраняется количество 0 и 1. В модели бильярдных шаров это означает, что на выходе то же количество шаров, что и на входе. Это хорошо отвечает сохранению массы в физике, и помогает продемонстрировать, что система не растратна. Логические цепочки 1) Обратимые логические цепочки:мы бы хотели иметь несколько видов простых обратимых вентилей, которые можно соединять, чтобы получить любую квантовую цепочку. Например, у нас есть обратимые n-битный вентиль f, и m-битный вентиль g. Соединив их k выходов f с k входами g, мы получим новую (n+m-k)-битную цепочку. И в таких соединениях важно, чтобы промежуточные цепочки также были обратимыми — так чтобы не создавался промежуточный мусор (физически, это означает сохранение энтропии — т. е. мы не теряем информацию в пространство. Для квантовой системы это означает предотвращение декогеренции).
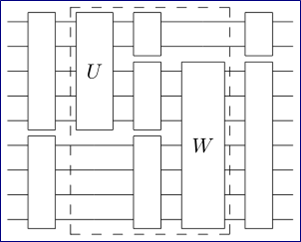
И, можно показать, что, например, вентили Тоффоли — универсальны, и не производят «мусора» - т. е. подходят для наших целей. Квантовые цепочки В реальных КК физическое соединение к. вентилей — это большая инженерная проблема, и именно здесь может возникнуть декогеренция. Есть теорема, что 1-кубитный вентиль сдвига фазы, и 2-кубитный CNOT – составляют универсальную систему. Однако, эта универсальность слабее, чем в классическом случае — она лишь утверждает, что с их помощью можно аппроксимировать работу любой n-битной обратимой цепочки с произвольной точностью. Многие важные числовые задачи сводятся к унитарному преобразованию на конечномерном пространстве (например, дискретное преобразование Фурье — разложение функции на коэффициенты синусоид, т. е. на спектр. Оно используется в спектральном анализе, сжатии данных, решении частных дифференциальных уравнений, умножении полиномов). В принципе, чтобы реализовать это с помощью к. цепочки, нужно всего лишь подготовить n-кубитное состояние ψ в качестве соответствующей суперпозиции базисных состояний — на вход; и измерить выход. Но тут две проблемы: · невозможно измерить фазу ψ в любом вычислительном базисе, так что невозможно считать полный ответ (это так по Природе измерения в КМ) · нет эффективного способа подготовить начальное состояние ψ (потому что нам нужно начальное состояние |x,0>=|x1,...,xm,0,...,0> - а получается всегда смешанное состояние, а не чистые нули. Нули — для промежуточных входов-выходов) Несмотря на это, DFT используются как промежуточные этапы в других к. цепочках. А начальное состояние берётся как некоторое смешанное состояние, близкое к идеальному в некоторой подходящей метрике. Варианты квантового компьютера: В зависимости от того, на какие базовые элементы раскладывается вычисление, есть 4 основные модели: 1. Массив к. вентилей — вычисление раскладывается в последовательность 1,2-кубитных к. вентилей. (разработан David Deutsch, 1989) 2. Однонаправленный КК — вычисление раскладывается на последовательность 1-кубитных измерений над сильно запутанным начальным состоянием (кластерным состоянием). Однонаправленный — потому что измерение уничтожает предыдущее состояние. Выбор базиса для последующих измерений зависит от результата предыдущих — поэтому они не могут быть выполнены одновременно. 3. Адиабатический КК — основан на идее квантового отжига. Это метод нахождения глобального минимума функции среди некоторого набора решений-кандидатов. Текущее решение-кандидат случайным образом заменяется его соседом, если в том состоянии «энергия» (оптимизируемый функционал) меньше. Процесс регулируется параметром «напряжённость поля туннелирования», отвечающим за размер «просматриваемой» области. Изначально поле туннелирования сильное, поэтому поиск происходит по всему пространству. Потом напряжённость уменьшается, система оседает в нескольких состояниях с наименьшими энергиями. Если повезёт, она найдёт глобальный минимум и там останется. В пределе мы получаем систему в одном из основных состояний. Адиабатический КК позволяет избежать проблемы декогеренции: поскольку система находится в основном состоянии, она имеет мало вероятности перейти в состояние с большей энергией, если температура среды достаточно низка. 4. Топологический КК — вычисление раскладывается в переплетение анионов в двумерной решётке — квазичастиц, чьи мировые линии, переплетаясь, формируют решётку из к. вентилей. Такой КК устойчивее моделей на пойманных в ловушку частицах — частицы подвержены декогеренции, а переплетения сохраняют свою топологическую структуру. Пока это только теоретическая модель, предложенная Алексеем Китаевым в 1997. Все эти четыре модели вычислительно эквивалентны — одну можно представить как другую. Физическая реализация: 1) КК на ионных ловушках — ионы подвешены в пространстве с помощью ЭМ-полей. Кубиты хранятся в стабильных электронных состояниях ионов, и к. информация передаётся через коллективное квантизованное движение ионов в общей ловушке. Воздействием лазеров осуществляется связь состояний кубитов. Компоненты: а. Кубит: ион в двух состояниях — основное состояние, и возбуждённое состояние. б. Инициализация: лазер соединяет ион с некоторыми возбуждёнными состояниями, которые постепенно скатываются к одному состоянию, которое не связано лазером. Когда ион достигает этого состояния, у него нет возбуждённых уровней, с которыми связываться в присутствии этого лазера — и он остаётся в этом состоянии. В любом другом состоянии, лазер будет продолжать возбуждать ион, пока он не скатится к тому, которое не взаимодействует с лазером. Многообещающие в смысле масштабируемости КК схемы предлагают переносить ионы в пространственно разделённые участки в массиве ионных ловушек, и создавать большие спутанные состояния с помощью фотонно связанных ионных цепочек. Это делает КК на ионных ловушках самой перспективной схемой масштабируемого, универсального КК. в. Измерение: применяем лазер к иону, который связан только с одним состоянием кубитов. Когда ион коллапсирует в это состояние во время измерения, лазер возбудит его, и тот, распадаясь из этого состояния, испустит фотон. Этот фотон можно уловить камерой. г. Произвольное вращение одного кубита: с помощью квадрипольного переноса в оптических кубитах. д. 2-кубитные вентили с запутанностью: есть CNOT, предложенные Цираком и Золлером в 1995, и другие, более надёжные схемы, реализованные экспериментально. е. Масштабируемые схемы ловушек: ионы могут быть выделены из региона взаимодействия в индивидуальные регионы-хранилища, и перенесены обратно без потери к. информации. Также ионы можно заставить поворачивать на Т-образных перекрёстках, составляя таким образом 2-мерные массивы ловушек. Уже есть технологии выпуска соответствующих полупроводников — что делает «ионную ловушку на чипе» реальностью.
2) Оптические решётки (2005) — формируются интерференцией пере Проблемы: решётка, образованная картиной интерференции очень нестабильна при изменении угла между лазерами (а это нужно для управления системой)
Применяя локальные магнитные поля, мы можем реализовать CNOT; а за счёт узкого зазора между двумя точками можно модулировать их связь, и реализовать Swap. 4) Линейный оптический кк —на фотонах, управляемых линейными элементами: зеркалами, расщепителями потока и сдвигами фазы. Этот подход позволяет легко реализовать суперпозицию (интерференция фотонов), а также к. вентили, и объединять их в цепочки. Также, ЛОКК позволяют рассматривать в одной модели к. вычисления и к. коммуникацию — это хорошо для реализации к. информационных систем. Проблема: в недетерминистских схемах ЛОКК ресурсно неэффективен — нужно много оптических элементов и шагов, чтобы реализовать ту или иную цепочку (а для детерминистских — зачем он нафиг нужен?). Предложена схема KLM, которая за счёт прогнозирующих измерений фотодетекторами может снизить требования к ресурсам — делая масштабируемую систему на ЛОКК более практичной. Пока что самые большие сконструированные квантовые регистры имеют немногим более десятка связанных кубит. Кубитное хранилище:в 2008 учёным удалось на 1.75 секунды передать к. состояние суперпозиции из «вычислительного» спина электрона — в атомный кубит «памяти». Это первый относительно приемлемый эксперимент по созданию к. хранилища данных. Недавно это время довели до 3 часов при сверхнизких температурах, и 39 мин. при комнатных.
Описание алгоритмов:
Поиск по сайту: |

 секающихся лазерных лучей, создающих периодическую в пространстве картину поляризации — в её минимумах и попадают в ловушку атомы. Двигаются атомы при помощи квантового туннелирования.
секающихся лазерных лучей, создающих периодическую в пространстве картину поляризации — в её минимумах и попадают в ловушку атомы. Двигаются атомы при помощи квантового туннелирования.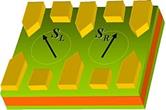 3) Квантовые точки (Daniel Loss и David P. DiVincenzo, 1997)- один кубит можно представить в виде электрона в двухъямном потенциале, так что |0> означает нахождение его в левой яме, а |1> — в правой.
3) Квантовые точки (Daniel Loss и David P. DiVincenzo, 1997)- один кубит можно представить в виде электрона в двухъямном потенциале, так что |0> означает нахождение его в левой яме, а |1> — в правой.