 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Кинетика специфического кислотно-основного катализа
Решение кинетической задачи рассмотрим на примере реакций специфического кислотного катализа. Пусть взаимодействие субстрата (S) и катализатора (H3O+) протекает по схеме:
Скорость лимитирующей стадии определяет скорость протекания процесса: v = k2 cSH+, (6.18) где k2 = k’2·c Концентрация протонированного субстрата (c SH+) составляет какую–то долю (α) от исходной концентрации субстрата (cS0): α = cSH+/cS0 или cSH+ = α· cS0. (6.19)
Учитывая это, уравнение для скорости лимитирующей стадии будет равно: v = k2 α· cS0. (6.20)
Если равновесие в первой стадии реакции устанавливается быстро, то соотношение активностей реагентов практически не будет отличаться от равновесного и степень протонизации субстрата (α) можно оценить из константы равновесия первой стадии процесса:
где
Отсюда
где Учитывая то, что
Используя полученные уравнения, получим кинетическое уравнение для скорости реакции специфического кислотного катализа:
Как видно из уравнения определяемая из опытных данных эффективная константа скорости зависит от кислотности среды:
Проведем анализ уравнения . 1. Если равновесие первой стадии устанавливается быстро, то константа равновесия К достаточно большая величина по сравнению с 1, тогда 2. Если равновесие первой стадии устанавливается медленно, то константа равновесия (К) величина небольшая и слагаемым К·h0 в знаменателе можно пренебречь. В этом случае уравнение для эффективной константы скорости имеет вид:
После логарифмирования имеем:
где логарифм кислотности, взятый с обратным знаком функция кислотности, называется функцией кислотности Гаммета:
График, построенный в координатах Построив по экспериментальным данным график в координатах lgkэфф – рН, можно оценить значение произведения k2·K. Если известнаконстанта равновесия первой стадии, то можно определить k2.· 3. Если константа равновесия К – средняя величина, то уравнение для можно привести к виду прямой линии:
График, построенный по опытным данным в координатах
Поиск по сайту: |
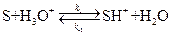 равновесная стадия процесса
равновесная стадия процесса лимитирующая стадия
лимитирующая стадия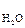
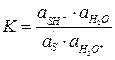 , или
, или  , (6.21)
, (6.21) - концентрация непротонированного субстрата,
- концентрация непротонированного субстрата, 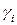 - соответствующие коэффициенты активности.
- соответствующие коэффициенты активности.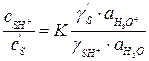 или
или  (6.22)
(6.22)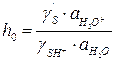 – кислотность среды.
– кислотность среды. получаем:
получаем: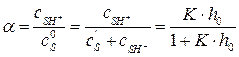 (6.23)
(6.23) , (6.24)
, (6.24)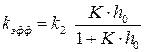 (6.25)
(6.25) .
.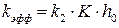 .
.
 , (6.26)
, (6.26)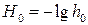 . (6.27)
. (6.27)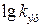 –
– 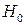 имеет тангенс угла наклона -1. Величину
имеет тангенс угла наклона -1. Величину 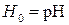 .
.
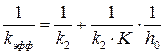 (6.28)
(6.28)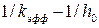 , в случае соответствия этой модели реальной кинетике процесса должен изображаться прямой линией. Зная угловой коэффициент прямой и отрезок на оси ординат, можно вычислить
, в случае соответствия этой модели реальной кинетике процесса должен изображаться прямой линией. Зная угловой коэффициент прямой и отрезок на оси ординат, можно вычислить 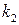 и К.
и К.