 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Интегралы от тригонометрических функций, умноженных на многочлен
Общее правило: за Пример 7 Найти неопределенный интеграл.
Интегрируем по частям:
Хммм, …и комментировать нечего. Пример 8 Найти неопределенный интеграл Это пример для самостоятельного решения Пример 9 Найти неопределенный интеграл Еще один пример с дробью. Как и в двух предыдущих примерах за
Интегрируем по частям:
Если возникли трудности или недопонимание с нахождением интеграла Пример 10 Найти неопределенный интеграл Это пример для самостоятельного решения. Подсказка: перед использованием метода интегрирования по частям следует применить некоторую тригонометрическую формулу, которая превращает произведение двух тригонометрических функций в одну функцию. Формулу также можно использовать и в ходе применения метода интегрирования по частям, кому как удобнее. Вот, пожалуй, и всё в данном параграфе. Почему-то вспомнилась строчка из гимна физмата «А синуса график волна за волной по оси абсцисс пробегает»….
Интегралы от обратных тригонометрических функций. Общее правило: за Напоминаю, что к обратным тригонометрическим функциям относятся арксинус, арккосинус, арктангенс и арккотангенс. Для краткости записи я буду называть их «арками» Пример 11 Найти неопределенный интеграл. Решаем.
Интегрируем по частям:
Интеграл Таким образом, помимо «чистого» интегрирования по частям нередко требуется применять и другие методы, приёмы решения. Пример 12 Найти неопределенный интеграл. Это пример для самостоятельного решения И заключительный пример сегодняшнего урока под счастливым номером тринадцать: «арк», умноженный на многочлен. Он сложнее, и предназначен для Пример 13 Найти неопределенный интеграл. Что касаемо интегрирования по частям, почти всё разобрали. Рассмотренный метод часто применяется в комбинации с другими приёмами решения интегралов. Читатели с хорошими навыками могут ознакомиться с такими примерами на уроке Сложные интегралы. А сейчас, как любила говорить моя учительница по математике, пора кончать. Желаю успехов! Решения и ответы: Пример 3:Решение:
Пример 4:Решение: Интегрируем по частям: Пример 6:Решение: Дважды интегрируем по частям: Пример 8:Решение: Интегрируем по частям: Пример 10:Решение: Интегрируем по частям: Примечание: Здесь мы использовали известную тригонометрическую формулу двойного угла Похожим способом также решаются интегралы вроде Пример 12: Решение:
Интегрируем по частям: Пример 13: Решение: Интегрируем по частям: Примечание: Если возникли трудности с интегралом Вы выполнили проверку? Может я и ошибся где… ;) Автор: Емелин Александр
Высшая математика для заочников и не только >>> (Переход на главную страницу) Как можно отблагодарить автора?
На данном уроке мы рассмотрим интегралы от тригонометрических функций, то есть начинкой интегралов у нас будут синусы, косинусы, тангенсы и котангенсы в различных комбинациях. Все примеры будут разобраны подробно, доступно и понятно даже для чайника. Для успешного изучения интегралов от тригонометрических функций Вы должны хорошо ориентироваться в простейших интегралах, а также владеть некоторыми приемами интегрирования. Ознакомиться с этими материалами можно на лекциях Неопределенный интеграл. Примеры решений и Метод замены переменной в неопределенном интеграле. А сейчас нам потребуются: Таблица интегралов, Таблица производных и Справочник тригонометрических формул. Все методические пособия можно найти на страницеМатематические формулы и таблицы. Рекомендую всё распечатать. Особо заостряю внимание на тригонометрических формулах, они должны быть перед глазами – без этого эффективность работы заметно снизится. Но сначала о том, каких интегралов в данной статье нет. Здесь не найдется интегралов вида При нахождении интегралов от тригонометрических функций используется ряд методов:
Поиск по сайту: |
 всегда обозначается многочлен
всегда обозначается многочлен


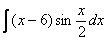
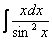


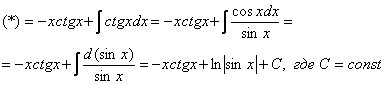
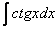 , то рекомендую посетить урок Интегралы от тригонометрических функций.
, то рекомендую посетить урок Интегралы от тригонометрических функций.
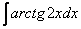



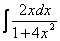 найден методом подведения функции под знак дифференциала, можно использовать и метод замены в «классическом» виде. Аналогичный пример мы разбирали на уроке Метод замены переменной в неопределенном интеграле.
найден методом подведения функции под знак дифференциала, можно использовать и метод замены в «классическом» виде. Аналогичный пример мы разбирали на уроке Метод замены переменной в неопределенном интеграле.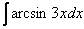

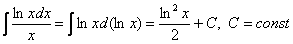
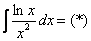

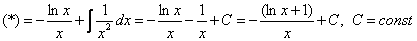
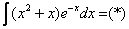

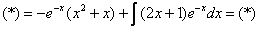
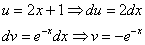
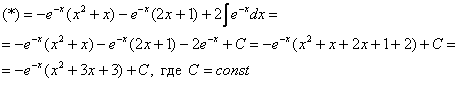
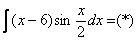
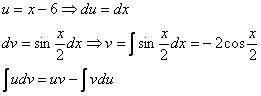
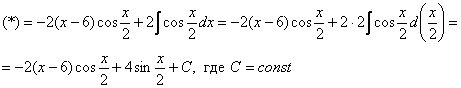
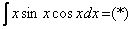
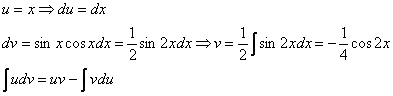
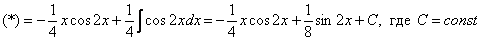
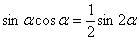 . Её можно было использовать и сразу:
. Её можно было использовать и сразу: 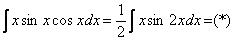 , а потом интегрировать по частям.
, а потом интегрировать по частям.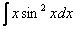 ,
,  – в них необходимо (сразу или в ходе решения) понизить степень синуса (косинуса) с помощью соответствующих формул. Более подробно – см. Интегралы от тригонометрических функций.
– в них необходимо (сразу или в ходе решения) понизить степень синуса (косинуса) с помощью соответствующих формул. Более подробно – см. Интегралы от тригонометрических функций.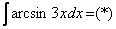
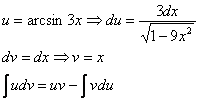
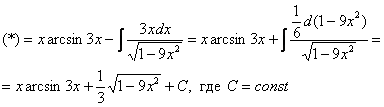
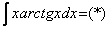


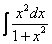 , то следует посетить урок Интегрирование некоторых дробей.
, то следует посетить урок Интегрирование некоторых дробей. 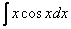 ,
, 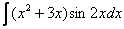 – косинус, синус, умноженный на какой-нибудь многочлен (реже что-нибудь с тангенсом или котангенсом). Такие интегралы интегрируются по частям, и для изучения метода посетите урок Интегрирование по частям. Примеры решений.Также здесь не найдется интегралов с «арками» – арктангенсом, арксинусом и др., они тоже чаще всего интегрируются по частям.
– косинус, синус, умноженный на какой-нибудь многочлен (реже что-нибудь с тангенсом или котангенсом). Такие интегралы интегрируются по частям, и для изучения метода посетите урок Интегрирование по частям. Примеры решений.Также здесь не найдется интегралов с «арками» – арктангенсом, арксинусом и др., они тоже чаще всего интегрируются по частям.