 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
II. Описание установки
Схема установки для определения скорости звука в воздухе представлена на рис .6 В длинной трубе размещается неподвижный источник звука и подвижный приёмник. В отрезке трубы между ними и возбуждается с помощью генератора ГЗ-34 стоячие волны. Частота определяется по шкале генератора и с помощью частотомера. На экране осциллографа С1-4 наблюдают принимаемый сигнал. При перемещении приемника сигнал на экране осциллографа периодически меняется, принимая поочередно минимальные и максимальные значения. Положения приемника в трубе, при которых наблюдаются два ближайших максимума, отличаются на половину длины волны
III. Измерения.
IV. Литература. 1. Пейн Г. Физика колебаний и волн. – М.: Мир, 1979, с. 100-121, с. 157-164. 2. Сивухин Д.В. Общий курс физики. – Механика. - М.: Наука, 1979, с. 81-85. ОПРЕДЕЛЕНИЕ СКОРОСТИ РАСПРОСТРАНЕНИЯ УЛЬТРАЗВУКА В ТВЕРДЫХ ТЕЛАХ
Краткая теория. Звуковые волны представляют собой процесс распространения механических колебаний в упругих средах. При рассмотрении акустических задач надо все среды (не только газы, но и жидкости и твердые тела) рассматривать как среды, обладающие определенной сжимаемостью. В акустике приходится отказываться от таких идеализированных понятий классической механики как абсолютно твердое тело или несжимаемая жидкость. Скорость распространения звуковых колебаний в среде зависит от плотности среды адиабатической сжимаемости
где В твердых телах могут распространяться как продольные, так и поперечные волны. Упругие свойства изотропных твердых тел описываются тремя величинами: модулем Юнга Скорость звука в твердом теле может быть рассчитана по формуле подобной (1)
где
Скорость распространения поперечных или сдвиговых волн определяется соотношением:
Величины
Поэтому для описания упругих свойств изотропного твердого тела достаточно использовать только две из трех этих величин. Измерение скорости распространения продольных и сдвиговых волн в образцах твердых тел используют для определения упругих констант материалов. Используя соотношения (3), (4), (5), коэффициент Пуассона можно выразить через отношение скорости
В кинематическом отношении распространение упругих колебаний в среде описывается уравнением бегущей волны. В одномерном случае (зависимость параметров от данной координаты) плоская ультразвуковая волна, распространяющаяся в положительную сторону оси
где
где
Она и представляет собой скорость распространения ультразвука в упругой среде. В обычных условиях скорость ультразвука в воздухе составляет 330 м/с, в воде 1500 м/с, в кварце 5700 м/с, в стали 6000 м/с. Кроме смещения колебания частиц среды можно характеризовать так называемой колебательной скоростью, которая находится дифференцированием по времени соотношения (7):
Скорость частиц не связана со скоростью распространения звука и обычно она много меньше
Поиск по сайту: |

 . Таким образом, определение длины волны при выбранной частоте производится в следующем порядке: устанавливают приёмник в трубе в такое положение, чтобы на экране осциллографа наблюдался максимум, замечают это положение на шкале приборов (трубы). Затем смещают приемник в ту или другую сторону до тех пор, пока на экране снова не будет наблюдаться максимум. По шкале, расположенной на трубе, определяют величину смещения приемника равную
. Таким образом, определение длины волны при выбранной частоте производится в следующем порядке: устанавливают приёмник в трубе в такое положение, чтобы на экране осциллографа наблюдался максимум, замечают это положение на шкале приборов (трубы). Затем смещают приемник в ту или другую сторону до тех пор, пока на экране снова не будет наблюдаться максимум. По шкале, расположенной на трубе, определяют величину смещения приемника равную  и
и
 (1)
(1) - модуль объемной упругости. В таком виде формулу (1) обычно используют для расчета скорости распространения продольных звуковых волн в жидкостях и газах.
- модуль объемной упругости. В таком виде формулу (1) обычно используют для расчета скорости распространения продольных звуковых волн в жидкостях и газах. , модулем сдвига
, модулем сдвига  и коэффициента Пуассона
и коэффициента Пуассона  . Модуль Юнга характеризует упругие свойства твердого тела при изменении линейных размеров (растяжения и сжатия), модуль сдвига - при поперечных смешениях слоев друг относительно друга. Коэффициент Пуассона представляет собой отношение поперечной деформации твердого стержня и продольной, т.е. относительного поперечного сжатия к относительному удлинению, вызванному продольным напряжением.
. Модуль Юнга характеризует упругие свойства твердого тела при изменении линейных размеров (растяжения и сжатия), модуль сдвига - при поперечных смешениях слоев друг относительно друга. Коэффициент Пуассона представляет собой отношение поперечной деформации твердого стержня и продольной, т.е. относительного поперечного сжатия к относительному удлинению, вызванному продольным напряжением. (2)
(2) - эффективный модуль упругости для данного типа волн, он зависит также от размеров образца, точнее, от соотношения между поперечными размерами образца и длиной волны в образце. Если поперечные размеры существенно превышают длину волны, скорость распространения продольных волн определяется соотношением:
- эффективный модуль упругости для данного типа волн, он зависит также от размеров образца, точнее, от соотношения между поперечными размерами образца и длиной волны в образце. Если поперечные размеры существенно превышают длину волны, скорость распространения продольных волн определяется соотношением: (3)
(3) (4)
(4) (5)
(5)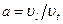
 (6)
(6)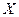 , описывается формулой:
, описывается формулой: (7)
(7)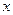 - смешение колеблющихся частиц относительно положения равновесия,
- смешение колеблющихся частиц относительно положения равновесия,  - амплитуда,
- амплитуда,  - циклическая частота,
- циклическая частота,  - волновое число. Формулу (7) можно записать в виде:
- волновое число. Формулу (7) можно записать в виде: (8)
(8)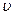 - фазовая скорость, которая определяется соотношением:
- фазовая скорость, которая определяется соотношением: (9)
(9) (10)
(10)