 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Определение модуля ЮнгаСтр 1 из 6Следующая ⇒
Раздел: «Изучение деформаций» Издательство Тюменского государственного университета, 1999
Работа утверждена на заседании кафедры механики многофазных систем 06.07.1998 г.
Методические указания, предназначенные для студентов первого курса физического факультета, полностью соответствуют действующим программам курса общей физики и физического практикума. Данные методические указания отличаются доходчивостью и ясностью изложения основных вопросов одного из важнейших разделов курса механики, описывающего деформации Экспериментальная часть методических указаний написана в соответствии с техническими характеристиками нового класса лабораторных работ по курсу механики.
Рецензент: зав. каф. радиофизики, к.ф.-м.н. В.А. Михеев
© Тюменский государственный университет, 1999. © Семихин В. И., Семихина Л.П., Зырянова М.В. 1999.
ИЗУЧЕНИЕ УПРУГОСТИ ТВЕРДОГО ТЕЛА.
Определение модуля Юнга.
Принадлежности: прибор, линейка, штангенциркуль, исследуемый стержень.
Изменение формы или объема твердого тела под действием внешних сил называется деформацией. Упругой называется деформация, исчезающая с прекращением действия силы. Свойство материала восстанавливать свою форму и объем называется упругостью. Деформация, остающаяся в теле после прекращения действия сил, называется остаточной, или пластической деформацией. Остаточная деформация характеризует свойство, называемое пластичностью. Упругость и пластичность присущи всем твердым телам. Деформация, возникающая в телах в зависимости от действия силы, подразделяется на следующие виды: растяжение, сжатие, сдвиг, кручение, изгиб.
I. Растяжение.
Деформацией сжатия подвергаются тела, к которым приложены силы, направленные по одной прямой навстречу друг другу, при этом происходит уменьшение длины тела и увеличение поперечного сечения (рис. 2). Деформацию сжатия испытывают столбы, колонны, стены, фундаменты домов и др.
III. Сдвиг. Часто тела подвергаются боковому действию. При этом, возникающие силы стремятся сместить одну его часть относительно другой. Возникающая деформация в этом случае называют сдвигом (рис. 3). Деформацию сдвига подвергаются болты и заклепки, соединяющие отдельные конструкции при боковых нагрузках.
Если один конец стержня закрепить, а к другому концу приложить пару сил, действующих в плоскости, перпендикулярно оси стержня, он деформируется. Этот вид деформации называется деформацией кручения. При деформации кручения отдельные слои тела остаются параллельными между собой, но повернутыми друг относительно друга (рис. 4). Деформации кручения подвергаются валы машин, передающие вращающий момент, болты при завинчивании гаек.
Детали, у которых один конец закреплен, а к другому приложена сила, изгибаются (рис. 5). Прямолинейная ось детали превращается в криволинейную. Наибольший прогиб в направлении, перпендикулярном оси, называют стрелой прогиба. Деформации изгиба подвергаются детали, подпертые с двух сторон и нагруженные между опорами (рис. 6). При деформации изгиба наружные слои вещества В случае, когда необходимо, чтобы тело сохраняло свою форму, используют упругую деформацию. При изготовлении деталей ковкой, штамповкой, волочением, прокатом, используют пластическую деформацию. Упругая деформация описывается законом, установленным Гуком. По закону Гука величина деформации пропорциональна действующей силе.
где Рассмотрим закон Гука применительно к деформации растяжения. Представим себе однородный стержень длиной Под действием силы
где Обычно деформацию тел характеризую не абсолютной деформацией
Закон Гука для деформации растяжения можно сформулировать следующим образом: относительное удлинение в пределах упругости пропорционально напряжению. Чаще упругие свойства материала характеризуются величиной, обратной коэффициенту упругости:
которую называют модулем Юнга. Подставим в (3) вместо
Из формулы имеем:
Если бы стержень подвергался такой деформации, что его длина возросла бы в двое, т.е. численно равная напряжению, при котором относительное удлинение стержня равно 1. Таков физический смысл модуля Юнга. При упругой деформации изгиба, величина деформации определяется стрелой прогиба
где
Целью данной работы является определение величины модуля упругости из деформации изгиба прямоугольных стержней.
ОПИСАНИЕ МЕТОДА ИЗМЕРЕНИЙ.
Для определения упругости
ПОРЯДОК ВЫПОЛНЕНИЯ РАБОТЫ.
Таблица 1.
Таблица 2.
ЛИТЕРАТУРА.
КОНТРОЛЬНЫЕ ВОПРОСЫ.
Поиск по сайту: |
 Деформации растяжения подвергаются тела, к которым приложены две силы, направленные по одной прямой в противоположные стороны, при этом увеличивается длина тела, не сохраняется сечение тела (рис. 1). Деформацию растяжения испытывают тросы, канаты, цепи в подъемных транспортных устройствах и др.
Деформации растяжения подвергаются тела, к которым приложены две силы, направленные по одной прямой в противоположные стороны, при этом увеличивается длина тела, не сохраняется сечение тела (рис. 1). Деформацию растяжения испытывают тросы, канаты, цепи в подъемных транспортных устройствах и др. II. Сжатие.
II. Сжатие.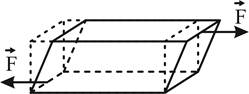
 IV. Кручение.
IV. Кручение.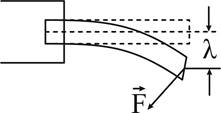 V. Изгиб.
V. Изгиб.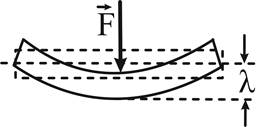 детали на вогнутой стороне подвергаются сжатию, а выпуклой — растяжению. Между ними лежит слой, который изменил только свою форму, но длина осталась без изменения. Этот слой называется нейтральным слоем. Вблизи от нейтрального слоя вещества почти не испытывают сжатия или растяжения. Поэтому сплошные детали, подвергающиеся изгибу, заменяют трубами, балки делают тавровыми (в виде T) или двутавровыми (в виде Н). Это облегчает вес конструкции и экономит металл. По этому пути шло развитие в природе. Кости животных, стебли растений имеют трубчатое строение.
детали на вогнутой стороне подвергаются сжатию, а выпуклой — растяжению. Между ними лежит слой, который изменил только свою форму, но длина осталась без изменения. Этот слой называется нейтральным слоем. Вблизи от нейтрального слоя вещества почти не испытывают сжатия или растяжения. Поэтому сплошные детали, подвергающиеся изгибу, заменяют трубами, балки делают тавровыми (в виде T) или двутавровыми (в виде Н). Это облегчает вес конструкции и экономит металл. По этому пути шло развитие в природе. Кости животных, стебли растений имеют трубчатое строение. (1)
(1) - коэффициент пропорциональности, постоянная величина для данного твердого тела.
- коэффициент пропорциональности, постоянная величина для данного твердого тела. с площадью поперечного сечения
с площадью поперечного сечения  , один конец которого закреплен, а к другому приложена сила
, один конец которого закреплен, а к другому приложена сила  , (рис. 7).
, (рис. 7). . Величина
. Величина  , приложенной к стержню, длине стержня
, приложенной к стержню, длине стержня  (2)
(2)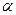 - коэффициент линейного растяжения или упругости. Это одна из формулировок закона Гука для деформации растяжения.
- коэффициент линейного растяжения или упругости. Это одна из формулировок закона Гука для деформации растяжения.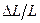 . Так как равные силы у стержней одной длины и одного материала, но разного сечения вызывают неодинаковые деформации, то вводят величину называемую напряжением:
. Так как равные силы у стержней одной длины и одного материала, но разного сечения вызывают неодинаковые деформации, то вводят величину называемую напряжением:  т. е. силу, приходящуюся на единицу площади. Тогда формула (2) принимает вид:
т. е. силу, приходящуюся на единицу площади. Тогда формула (2) принимает вид: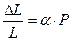 (3)
(3) (4)
(4) , получаем
, получаем (5)
(5) (6)
(6) и относительное удлинение стало бы
и относительное удлинение стало бы  , то получилось бы
, то получилось бы  , т. е. модуль Юнга есть величина,
, т. е. модуль Юнга есть величина, , т. е. перемещением нейтрального слоя под действием сил. Стрела прогиба
, т. е. перемещением нейтрального слоя под действием сил. Стрела прогиба  (7)
(7)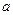 - ширина стержня,
- ширина стержня,  - высота. Из формулы (7) определяем
- высота. Из формулы (7) определяем (8)
(8)
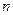 раз.
раз.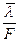 для точки на графике, отстоящей достаточно далеко от начала координат.
для точки на графике, отстоящей достаточно далеко от начала координат. .
.