 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
ОСНОВНЫЕ ЕДИНИЦЫ ИЗМЕРЕНИЯ ПОЛЯ ИЗЛУЧЕНИЯ⇐ ПредыдущаяСтр 23 из 23
Для характеристики поля излучения в практических задачах часто используется поток ионизирующих частиц или флюенс ионизирующих частиц(то есть перенос) – это отношение числа ионизирующих частиц dN, проникающих в элементарную сферу, к площади центрального сечения dS этой сферы:
Как общепринято в физике, под dN понимают как дифференциал ожидаемого значения числа частиц N. При этом дифференциал в знаменателе, с одной стороны, мал по сравнению с изменением поля излучения, с другой стороны, достаточно велик, чтобы можно было зарегестрировать много частиц. При практических измерениях под элементарной следует понимать такую сферу, в пределах объема которой характеристики поля излучения можно считать неизменными.
Единица флюенса частиц в СИ: м-2, предпочтительная см-2 , т.е. Плотностью потока частиц называют отношение потока частиц dФ за некоторый промежуток времени dt к этому промежутку времени:
Ј= Потоком энергии излучения называется отношение энергии dE частиц или квантов ионизирующего излучения, проникающих в объем элементарной сферы с площадью поперечного сечения dS, к этой площади:
F= Интенсивностью излучения (плотностью потока энергии) называется отношение потока энергии излучения dF частиц или квантов ионизирующего излучения за некоторый промежуток времени dt к этому промежутку времени: I=
Интеграл интенсивности излучения по времени назван количеством излучения (Копенгаген, 1953 год). Эта физическая величина получила название «доза». Введенные в этом параграфе характеристики поля излучения – флюенс частиц, плотность потока частиц и интенсивность излучения – положительные скалярные величины. Как эти величины даны здесь, они являются интегральными характеристиками поля и не дают представления об энергетическом и угловом распределениях излучения. Более детально поле излучения можно описать дифференциальными характеристиками. . ВЕКТОРНЫЕ И СКАЛЯРНЫЕ ХАРАКТЕРИСТИКИ ПОЛЯ ИЗЛУЧЕНИЯ Имеются два вида полей – скалярные и векторные. Скалярное поле задается функцией положения φ (x, y, z), которая привязывает к каждой точке пространства определенное значение скаляра. Векторное поле задается векторной функцией F (x, y, z), которая приписывает каждой точке в некоторой заданной системе отсчета вектор.
Поиск по сайту: |
 .
.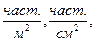 .
.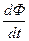 =
=  , (
, (  ).
). , (
, (  ,
, 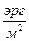 ,
,  ,
,  ).
). =
=  , (
, (  ,
,  ,
,  ,
,  ).
).