|
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Определение погрешностей при прямых измерениях
Надо измерить некоторую величину N. Пусть
есть величина, наиболее близкая к истинному значению, называемая средним значением величины N. Отсюда следует, что каждое физическое измерение должно быть повторено несколько раз. Разности
…………..
называются абсолютными ошибками или погрешностями отдельных измерений и могут быть и положительными и отрицательными. Для определения средней абсолютной ошибки результата берут среднее арифметическое абсолютных значений (модулей) отдельных ошибок, т.е.
Отношения Отношение средней абсолютной ошибки результата
Относительные ошибки принято выражать в процентах
Истинное значение
Не следует думать, что величина
Теория вероятностей дает более точную формулу для вычисления абсолютной ошибки результата, устанавливая понятие так называемой наиболее вероятной ошибки результата
В этом случае окончательное значение измеряемой величины
Если точность прибора такова, что при любом числе измерений получается одно и тоже число, лежащее где-то между делениями шкалы, то приведенный метод оценки погрешности неприменим. В этом случае измерение производится один раз и результат измерения записывается так:
где
Иногда положение какого-либо указателя, например, мениска столбика ртути в термометре, трудно различимо в пределах одного деления, равного, допустим, 0,1С. Тогда за предельную погрешность измерения берется значение всего деления, а не его половины. Часто в работах даются значения некоторых величин, измеренных заранее. В таких случаях абсолютную погрешность принимают равной ее предельной величине, т.е. равной половине единицы наименьшего разряда, представленного в числе. Например, если дана масса тела
Определение погрешностей для прямых измерений удобно производить по следующей таблице:
Поиск по сайту: |
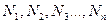 - результаты отдельных измерений, где n – число отдельных измерений. Среднее арифметическое из этих результатов, т.е.
- результаты отдельных измерений, где n – число отдельных измерений. Среднее арифметическое из этих результатов, т.е.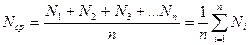
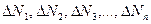 между средними значениями
между средними значениями  измеряемой величины и значениями
измеряемой величины и значениями  ;
; ;
; ;
;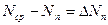 .
.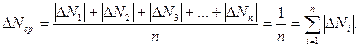
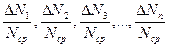 называются относительными ошибками отдельных измерений.
называются относительными ошибками отдельных измерений. к его среднему значению
к его среднему значению 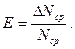
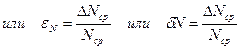
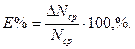

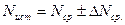
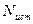 имеет два значения
имеет два значения 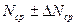 имеет только одно значение, а знак «+» или « - » показывает, что истинное значение измеряемой величины находится в интервале
имеет только одно значение, а знак «+» или « - » показывает, что истинное значение измеряемой величины находится в интервале .
.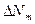 :
:
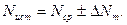
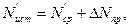
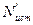 - искомый результат измерения;
- искомый результат измерения;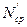 - средний результат, равный среднему арифметическому из двух значений, соответствующих соседним делением шкалы, между которыми заключено остающееся неизвестным истинное значение измеряемой величины.
- средний результат, равный среднему арифметическому из двух значений, соответствующих соседним делением шкалы, между которыми заключено остающееся неизвестным истинное значение измеряемой величины.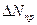 - предельная погрешность, равная половине цены деления шкалы прибора.
- предельная погрешность, равная половине цены деления шкалы прибора.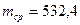 г, то
г, то  г, следовательно,
г, следовательно,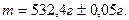


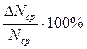



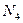 …
…
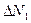
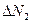
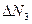
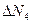 …
…