 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Получение фундаментальных величинСтр 1 из 3Следующая ⇒
Под измерением понимается сравнение измеряемой величины с другой величиной, принятой за единицу измерения. При прямых измерениях определяемая величина сравнивается с единицей измерения непосредственно или при помощи измерительного прибора, проградуированного в соответствующих единицах. К этим измерениям относятся измерения длины линейкой, штангенциркулем плитками Иогансона. Плитка Иогансона представляет собой хорошо отполированную плоскопараллельную пластинку определенной толщины (концевая мера). Складывая эти пластинки друг с другом, получают разные эталоны толщины. При косвенных измерениях измеряемая величина определяется (вычисляется) из результатов прямых измерений других величин, которые связаны с измеряемой величиной определенной функциональной зависимостью. Примерами косвенных измерений могут служить измерения скорости равномерного (или равноускоренного) движения по измерениям длины пройденного пути и промежутков времени; измерения плотности тела по измерениям массы и объема тела и т. п. При измерении любой физической величины обыкновенно приходится выполнять три последовательные операции: 1) проверку и установку приборов, 2) наблюдение их показаний и отсчет, 3) вычисление искомой величины из результатов измерений и оценку погрешности. При измерении любой величины мы никогда не получаем истинного значения этой величины, т. е. результат измерения дает лишь приближенное значение. Это объясняется как принципиально ограниченной возможностью точности измерения, так и природой самих измеряемых объектов. Развитие измерительной техники привело к появлению разнообразных приборов, отличающихся своей точностью. Точность прибора — это свойство измерительного прибора, характеризующее степень приближения показаний данного измерительного прибора к действительным значениям измеряемой величины. Она связана с физическим явлением, на основе которого построен метод измерения, и с допусками при изготовлении отдельных частей прибора. Точность прибора либо задается классом точности прибора, либо указана в паспорте, прилагаемом к прибору. Погрешность, вносимая прибором при каждом отдельном измерении (приборная погрешность), связана с точностью прибора. Эта погрешность равна той доле деления шкалы прибора, до которой с уверенностью в правильности результата можно производить отсчет. Обычно, если нет оговорок в паспорте прибора, она равна цене наименьшего деления шкалы (точнее, ±0,5 цены наименьшего деления). Естественно, чем точнее прибор, тем меньше погрешность прибора. Повышая точность отсчета по шкале данного прибора, мы принципиально не можем изменить (увеличить) точность самого прибора. Например, производя измерения длины карандаша с помощью линейки (грубого прибора), разделенной на сантиметры, мы не изменим точности линейки, если будем рассматривать ее шкалу с помощью лупы. Действительно, несмотря на то, что отсчет с помощью лупы будет содержать большее число значащих цифр, точность результата измерения длины карандаша останется прежней, так как точность линейки не изменилась. (Штрихи линейки нанесены через один сантиметр, но середины штрихов при изготовлении могут быть несколько смещены.) Точность измерений обратно пропорциональна так называемой относительной погрешности измерений, определение которой будет дано ниже. Так как точность измерений всегда бывает ограниченной, то результат измерений дает нам не истинное значение измеряемой величины, а лишь приближенное. Погрешности результата измерений определяются разностью измеренной и истинной величин и будут зависеть от многих причин. Обычно стараются произвести измерения с наибольшей достижимой точностью. е. сделать погрешность измерения по возможности малой. Следует иметь в виду, что чем точнее мы хотим измерить ту или иную величину, тем труднее это сделать, тем больше времени потребуют эти измерения. Так, например, измерение толщины пластинки штангенциркулем можно производить с погрешностью 0,1 мм; измерение этой же толщины винтовым микрометром можно производить с погрешностью 0,005 мм. Применение компаратора — прибора, применяемого при измерении положения спектральных линий, — позволяет уменьшить погрешность измерений до 0,001 мм. Интерференционные методы позволяют производить измерения с погрешностью до 0,1 Повторные измерения одной и той же величины дают в общем случае результаты, несколько отличающиеся друг от друга даже тогда, когда они производились одним и тем же лицом, одним и тем же способом, посредством одних и тех же приборов. Любые измерения всегда производятся с какими-то погрешностями (ошибками). Погрешности разделяются на две группы: систематические и случайные . Систематические погрешности — погрешности, связанные с ограниченной точностью изготовления прибора (погрешностью прибора), неправильным выбором метода измерений, неправильной установкой прибора. Они также появляются, если пренебречь действием некоторых внешних факторов. Случайные погрешности вызываются большим числом случайных причин, действие которых на каждое измерение различно и не может быть заранее учтено. Типичным примером подобных погрешностей может служить так называемая ошибка параллакса (рис. 1), которая состоит в следующем. Для отсчета делений шкалы прибора необходимо, строго говоря, расположить глаз наблюдателя на перпендикуляре к шкале, проходящем через конец стрелки прибора или через край измеряемого предмета. Однако глаз человека не всегда может быть расположен точно на перпендикуляре. Поэтому при отсчетах мы будем получать, либо завышенные, либо заниженные значения (рис. 2).
Рис. 2. Ошибка параллакса при отсчете делений шкалы. Надежностью результата серии измерений называется вероятность Чем больше величина доверительного интервала ( Произвести измерения физических величин абсолютно точно невозможно, так как всякое измерение сопровождается той или иной ошибкой или погрешностью. Погрешности или ошибки измерений бывают систематические и случайные. Систематические ошибки происходят от несовершенства приборов для измерений, а также от недостаточно разработанной теории опыта (например, трудно учесть многие причины, влияющие на точность искомого результата: влияние среды, роль примесей, контакты с другими телами и т.п. – это так называемые объективные причины). Систематические ошибки дают отклонение результата от истинного значения только в одну сторону (или в сторону увеличения, или в сторону уменьшения). Систематических ошибок можно избежать путем изучения приборов, которыми пользуются при выполнении работ, полной разработкой теории опыта, а также введением соответствующих поправок в результат измерений. Случайные ошибки носят субъективный характер. Они могут происходить по вине экспериментатора: от несовершенства зрения, слуха или по другим причинам, которые заранее нельзя учесть. Случайные ошибки могут изменять результаты в обе стороны, по увеличивая, то уменьшая их. Иногда говорят о промахах или просчетах – это ошибки, возникающие в результате небрежности отсчета по приборам или неразборчивости в записи их показаний. Единственное средство устранить их: внимательно сделать повторное (контрольное) измерение. Эти ошибки в расчет не принимают. Исключить при измерениях случайные ошибки невозможно, но благодаря тому, что к случайным ошибкам можно применить законы теории вероятности, можно уменьшить влияние этих ошибок на окончательный результат измерений.
Поиск по сайту: |
 , т. е. при применении зеленого света до 0,0005 мм. Однако применение компаратора требует постоянства температуры измеряемого тела и самого компаратора — их приходится помещать в термостат, иначе тепловое расширение при изменении температуры даст большее изменение длины, чем может чувствовать прибор, и , таким образом, будут искажены результаты измерений. Применение интерферометров требует кроме термостатирования тщательной полировки поверхности предмета, жесткости основания установки (обычно монтаж производится на бетонном или чугунном основании) и т. д. Таким образом, проведение измерений с высокой точностью связано с большими экспериментальными трудностями, а следовательно, с затратами времени и труда. Поэтому не следует требовать от измерений большей точности, чем это необходимо. Инженер также не должен необоснованно уменьшать допуски на изготовление деталей и т. п.
, т. е. при применении зеленого света до 0,0005 мм. Однако применение компаратора требует постоянства температуры измеряемого тела и самого компаратора — их приходится помещать в термостат, иначе тепловое расширение при изменении температуры даст большее изменение длины, чем может чувствовать прибор, и , таким образом, будут искажены результаты измерений. Применение интерферометров требует кроме термостатирования тщательной полировки поверхности предмета, жесткости основания установки (обычно монтаж производится на бетонном или чугунном основании) и т. д. Таким образом, проведение измерений с высокой точностью связано с большими экспериментальными трудностями, а следовательно, с затратами времени и труда. Поэтому не следует требовать от измерений большей точности, чем это необходимо. Инженер также не должен необоснованно уменьшать допуски на изготовление деталей и т. п.
 того, что истинное значение а измеряемой величины попадает в данный доверительный интервал. Эта величина а выражается или в долях единицы, или м процентах.
того, что истинное значение а измеряемой величины попадает в данный доверительный интервал. Эта величина а выражается или в долях единицы, или м процентах.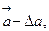
 ), т. е. чем больше задаваемая погрешность результата измерений
), т. е. чем больше задаваемая погрешность результата измерений  , тем с большей надежностью искомая величина а попадает в этот интервал.Измерить какую-либо величину – значит узнать, сколько раз заключается в ней однородная величина, принятая за единицу меры. Непосредственно измерять данную величину (прямое измерение) приходится очень редко. В большинстве случаев производят не прямые измерения данной величины, а косвенные – через величины, связанные с измеряемой физической величиной определенной функциональной зависимостью. Например, измерение ускорения силы тяжести производится по измерению длины маятника и времени его качания.
, тем с большей надежностью искомая величина а попадает в этот интервал.Измерить какую-либо величину – значит узнать, сколько раз заключается в ней однородная величина, принятая за единицу меры. Непосредственно измерять данную величину (прямое измерение) приходится очень редко. В большинстве случаев производят не прямые измерения данной величины, а косвенные – через величины, связанные с измеряемой физической величиной определенной функциональной зависимостью. Например, измерение ускорения силы тяжести производится по измерению длины маятника и времени его качания.