 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Вычисление определённого интеграла с помощью пакета Maxima
Определенный интеграл integrate(f, x, a, b), где f – подынтегральная функция, x – переменная интегрирования, a и b соответственно верхний и нижний пределы интегрирования. Примеры. Вычислить интеграл: 1) В вводной ячейке задаём команду (%i4) integrate((1+cos(x))^2,x,0,%pi); получаем результат (%o4) (3*%pi)/2. 2) (%i14) integrate(cos(2*x)*exp(-x),x,0,3); (%o14) (%e^(-3)*(2*sin(6)-cos(6)))/5+1/5 (%i15) %o14, numer; (%o15) 0.184874675854 Численное интегрирование выполняется функцией romberg или при помощи функций пакета quadpack. Пример. Вычислить интеграл В стоке меню выбираем кнопку Анализ → Integrate…(Рис. 7.2), в результате возникает вспомогательное окно для ввода подынтегральной функции и пределов интегрирования Интегрировать(Рис. 7.3), здесь же указывается режим интегрирования (численное), а также метод интегрирования romberg или quadpack.
Рис. 7.2
Рис. 7.3 Нажав на клавишу Okв рабочем окнепоявитсявводная ячейка и результат интегрирования (%i2) quad_qags(tan(x)/(sin(x)^2-5*cos(x)^2+4), x, %pi/4, acos(1/sqrt(3))); (%o2) [0.081093021621633,9.0031339740762459*10^-16,21,0] В ячейке вывода (%о2) массив результата вычисления содержит: 0.081093021621633 – приближённое значение интеграла; 9.0031339740762459*10^-16 – относительная погрешность вычислений; 21 – число интервалов разбиения; 0 – признак корректности вычислений (0 – без проблем). Примеры для самостоятельного решения Вычислить определённый интеграл с помощью пакета Maxima 1) 4) 7) Применение определённого интеграла 7.4.1. Вычисление площадей плоских фигур Прямоугольные координаты Известно, что определенный интеграл на отрезке представляет собой площадь криволинейной трапеции, ограниченной графиком функции f(x). Если график расположен выше оси Ох (см. рис. 7.4), т.е. f(x) > 0,
Рис. 7.4 то площадь имеет знак “+“ и в этом случае искомая площадь определяется формулой
Если график функции f(x) расположен ниже оси Ох (см. рис. 7.3), т.е. f(x) < 0,
Рис. 7.5 то площадь имеет знак “ - ” и Площадь фигуры, ограниченной кривыми y = f1 (x) и y = f2 (x) (при условии f2 (x) ≥ f1 (x) см. рис. 7.6), прямыми x = a и x = b может быть найдена с помощью определенных интегралов
Рис. 7.6. Примеры. 1. Вычислить площадь фигуры, ограниченной графиком функции y = sin x и осью Ох при
Рис. 7.7. Используя формулу (7.5), находим искомую площадь фигуры
2. Вычислить площадь фигуры, ограниченную линиями у = х, Изобразим данную фигуру (рис. 7.8)
Рис. 7.8. Находим пределы интегрирования: точка пересечения линий у = х,
3. Вычислить площадь фигуры, ограниченную линями Построим фигуру, площадь которой необходимо вычислить (рис. 7.9).
Рис. 7.9. Находим точку пересечения линий
Параметрические координаты Если криволинейная трапеция ограничена кривой, заданной параметри-чески
прямыми
где α и β определяются из равенств Примеры. 1. Найти площадь фигуры ограниченной эллипсом, который задан в параметри-ческой форме
Изображаем фигуру, площадь которой необходимо определить (рис. 7.10)
Рис. 7.10. Найдём четвёртую часть площади S, расположенной в первой четверти ко-ординатной плоскости (на рисунке она окрашена серым цветом). Здесь х изменяется от 0 до а и, следовательно, t изменяется от π / 2 до 0. По формуле (7.7) находим
= 2. Вычислить площадь фигуры, ограниченной одно аркой циклоиды и осью Ох. Циклоида есть траектория точки, расположенной на ободе колеса радиуса а , при равномерном качении колеса по оси Ох. При одном обороте колеса
Рис. 7.11. Уравнение циклоиды в параметрической форме имеет вид
При изменении
= = Полярные координаты В некоторых случаях вычисление площадей криволинейных фигур удобно проводить в полярных координатах. Полярная система координат определяется заданием точки О (полюс)луча Ор, исходящего из точки О (полярной оси) и масштаба для измерения длины. Положение точки М на плоскости определяется в полярной системе координат двумя числами: полярным радиусом
Рис. 7.12. Из рис. 7.10 видно, что независимо от расположения точки М на плоскости имеют место следующие формулы перехода от полярных координат ( и от декартовых к полярным: Найдём площадь криволинейного сектора.Пусть кривая АВ задана в полярных координатах уравнением
Рис. 7.13. Доказательство. Разобьем произвольно отрезок [α, β] иа п частей точками ол
где Следовательно, и площадь криволинейного сектора численно равна этому определенному интегралу:
Пример 1.Вычислить площадь фигуры, ограниченной полярной осью и первым витком спирали Архимеда:
Рис. 7.12. Решение. При изменении
Расстояние от точки С до полюса равно Пример 2.Второй закон Кеплера (закон площадей) о движении планет солнечной системы гласит: площадь, описываемая радиусом-вектором планеты, проведенном из центра Солнца, возрастает пропорционально времени. Пользуясь этим законом площадей, покажем, что скорость планеты VП в ближайшей к Солнцу точке орбиты П (перигелий) будет наибольшей, а в наиболее удалённой от Солнца точке А (афелий) – скорость будет наименьшей (рис. 7.15)
Рис. 7.15. Рассмотрим перемещение планеты в окрестностях точек А (афелий) и П (перигелий), по закону Кеплера площади секторов
где Из формулы для площади криволинейного сектора (7.8) следует, что
или
Отношение перемещения планеты
В результате
Поиск по сайту: |
 в символьном режиме (аналитически) вычисляется с помощью команды
в символьном режиме (аналитически) вычисляется с помощью команды

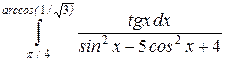


 (
( 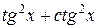 ) dx . 2)
) dx . 2) 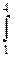 (
(  ) dx . 3)
) dx . 3)  ) dx . 5)
) dx . 5)  (
(  ) dx . 6)
) dx . 6)  (
(  ) dx .
) dx .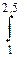 (
( 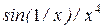 ) dx . 8)
) dx . 8)  (
(  ) dx . 9)
) dx . 9)  (
(  ) dx . 10)
) dx . 10)  (
(  ) dx . 11)
) dx . 11)  (
(  ) dx . 12)
) dx . 12)  (
(  ) dx . 13)
) dx . 13) 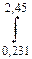 (
( 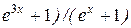 ) dx . 15)
) dx . 15) 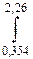 (
(  ) dx .
) dx .
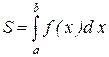 . (7.5)
. (7.5)
 .
. . (7.6)
. (7.6)
 . Построим данную фигуру (рис. 7.7)
. Построим данную фигуру (рис. 7.7)
 (кв. ед.)
(кв. ед.) , х = 2.
, х = 2.
 , следовательно, промежуток интегрирования -
, следовательно, промежуток интегрирования -  . По формуле (7.6) определяем площадь фигуры
. По формуле (7.6) определяем площадь фигуры (кв. ед.)
(кв. ед.)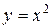 и
и 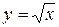 .
.
 , имеем
, имеем  или
или  , откуда
, откуда  . Из рисунка видно, что пределами интегрирования являются
. Из рисунка видно, что пределами интегрирования являются  . Определяем площадь фигуры, используя формулу (7.6)
. Определяем площадь фигуры, используя формулу (7.6) (кв. ед.)
(кв. ед.) ,
, и
и  и осью Ох, то её площадь определяется по формуле
и осью Ох, то её площадь определяется по формуле , (7.7)
, (7.7) и
и  .
. .
.
 =
= . Таким образом,
. Таким образом,  . Значит
. Значит  .
. центр колеса переместится на расстояние
центр колеса переместится на расстояние  (рис. 7.11).
(рис. 7.11).
 ,
, параметр t изменяется в пределах
параметр t изменяется в пределах  =
= =
= .
. (рис. 7.12), выражающим длину отрезка ОМ в выбранном масштабе, и полярным углом φ =
(рис. 7.12), выражающим длину отрезка ОМ в выбранном масштабе, и полярным углом φ =  .
.
 ) к декартовым (х, у) :
) к декартовым (х, у) : 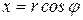 ,
,  ;
; ,
,  .
. ,
,  , причем функция
, причем функция  . (7.8)
. (7.8)
 , выберем на каждом частичном отрезке [
, выберем на каждом частичном отрезке [ 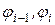 ] произвольно точку
] произвольно точку  (
(  ) и построим круговые секторы с радиусами
) и построим круговые секторы с радиусами  . В результате получим веерообразную фигуру, площадь которой приближенно равна площади S криволинейного сектора:
. В результате получим веерообразную фигуру, площадь которой приближенно равна площади S криволинейного сектора: ,
, . С другой стороны, площадь веерообразной фигуры является интегральной суммой для интеграла (7.8). Так как функция
. С другой стороны, площадь веерообразной фигуры является интегральной суммой для интеграла (7.8). Так как функция  непрерывна на отрезке [α, β ], то предел этой суммы при
непрерывна на отрезке [α, β ], то предел этой суммы при 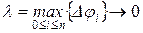 существует и равен интегралу (7.8).
существует и равен интегралу (7.8). .
. , где а — положительное число (рис. 7.12).
, где а — положительное число (рис. 7.12).
 от 0 до 2π полярный радиус описывает кривую, ограничивающую криволинейный сектор ОАВС. Поэтому по формуле (7.8) имеем
от 0 до 2π полярный радиус описывает кривую, ограничивающую криволинейный сектор ОАВС. Поэтому по формуле (7.8) имеем .
.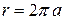 . Поэтому круг радиуса ОС имеет площадь π ∙OC2 = 4 π3 a2 = 3 ∙
. Поэтому круг радиуса ОС имеет площадь π ∙OC2 = 4 π3 a2 = 3 ∙  , т. е. площадь фигуры, ограниченной полярной осью и первым витком спирали Архимеда, равна 1/3площади круга с радиусом, равным наибольшему из полярных радиусов витка. К этому выводу пришел еще Архимед.
, т. е. площадь фигуры, ограниченной полярной осью и первым витком спирали Архимеда, равна 1/3площади круга с радиусом, равным наибольшему из полярных радиусов витка. К этому выводу пришел еще Архимед.
 и
и  равны между собой, т.е.
равны между собой, т.е. ,
, - площадь сектора, опирающегося на дугу
- площадь сектора, опирающегося на дугу 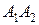 , длина этой дуги равна
, длина этой дуги равна  , аналогично
, аналогично  - площадь сектора, опирающегося на дугу
- площадь сектора, опирающегося на дугу 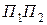 , длина этой дуги равна
, длина этой дуги равна  .
.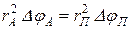
 , т.е.
, т.е.  . Здесь
. Здесь  в окрестности точек А и П орбиты. Разделим предыдущее равенство на промежуток времени
в окрестности точек А и П орбиты. Разделим предыдущее равенство на промежуток времени  .
. ,
,  .
. или
или  , откуда следует, что
, откуда следует, что .
.