 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Визначення довжини дуги плоскої кривої
Прямокутні координати Хай в прямокутних координатах задана плоска крива АВ, рівняння якої
Рис. 7.16. Довжина ламаної лінії, яка відповідає дузі M0Mn, може бути знайдена як сума З геометричних міркувань: Тоді
Приклад.Обчислити довжину дуги кубічної параболи Оскільки
= Якщо рівняння кривої задане параметрично, то з врахуванням правил обчислення похідної параметрично заданої функції, з формули (7.9) отримуємо
= де х = x(t), a = x(α) і у = у(t), b=y(β). Таким чином, якщо рівняння кривої задане в параметричній формі, то довжина кривої знаходиться по формулі
Приклад.Знайти довжину першої арки циклоїди
Знаходимо похідні
= = Якщо задана просторова крива , і х = x(t), у = y(t) и z = z(t), то
Полярні координати Хай крива задана в полярних координатах,
і довжину кривої знаходимо по формулі (7.10), виконавши відповідні перетворення
Тому = В результаті довжина кривої визначається формулою
Приклад.Знайти довжину кардіоїди
Рис. 7.17 може бути отримана як траєкторія точки кола С1, що котиться без ковзання по колу С того ж радіусу а. Коли φ пробігає проміжок (-π, +π) , кардіоїда описується повністю. Довжина її згідно (7.12) рівна
Таким чином, довжина кардіоїди дорівнює восьмикратному діаметру виробляючого круга. Обчислення об'єму тіла Обчислення об'єму тіла по відомих площах його поперечних Перетинів Хай є тіло об'єму V. Площа будь-якого поперечного перетину тіла S, відома як безперервна функція S = S(x). Розіб'ємо тіло на “шари” поперечними перетинами, що проходять через точки хi розбиття відрізання [а, b]. Оскільки на якому-небудь проміжному відрізку розбиття [xi-1, xi] функція S(x) безперервна, то набуває на нім найбільшого і найменшого значень. Позначимо їх відповідно Mi і mi.
Рис. 7.18 Якщо на цих найбільшому і найменшому перетинах побудувати циліндри із утворюючими, паралельними осі х, то об'єми цих циліндрів будуть відповідно рівні MiDxi і miDxi , тут Dxi = xi+1 - xi. Виробивши такі побудови для всіх відрізків розбиття, отримаємо циліндри, об'єми яких рівні відповідно При прагненні до нуля кроку розбиття l , ці суми мають загальну границю:
Таким чином, об'єм тіла може бути знайдений по формулі:
Недоліком цієї формули є те, що для знаходження об'єму необхідно знати функцію S(x), що вельми проблематично для тіл складної форми. Об'єм тіла обертання Розглянемо криву, задану рівнянням y = f(x). Передбачимо, що функція f(x) безперервна на відрізку [а, b]. Якщо відповідну їй криволінійну трапецію з підставами а і b обертати довкола осі Ох, то отримаємо так зване тіло обертання (рис. 7.19).
Рис. 7.19. Перетин цього тіла площиною, перпендикулярній осі Ох, проведеною через довільну точку х осі Ох ( Застосовуючи формулу (7.13) об'єму тіла, для якого відомі площі поперечних перетинів, отримуємо
Приклад.Визначити об'єм тіла, утвореного обертанням фігури, обмеженої лініями y = x2 , x = 1, x = 2 (рис. 7.20).
Рис. 7.20. Розв‘язання. За формулою (7.14) знаходимо
Поиск по сайту: |
 , де
, де  . Якщо
. Якщо 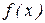 і
і  безперервні, то такі криві називаються гладкими. Під довжиною дуги АВ розуміється границя, до якої прагне довжина ламаної лінії, вписаної в цю дугу, коли число сторін ламаною необмежено зростає, а довжина найбільшої із сторін ламаною прагне до нуля.
безперервні, то такі криві називаються гладкими. Під довжиною дуги АВ розуміється границя, до якої прагне довжина ламаної лінії, вписаної в цю дугу, коли число сторін ламаною необмежено зростає, а довжина найбільшої із сторін ламаною прагне до нуля.
 , де
, де  - довжина сторони ламаною на ділянці
- довжина сторони ламаною на ділянці  (рис. 7.16). Тоді довжина дуги M0Mn дорівнює
(рис. 7.16). Тоді довжина дуги M0Mn дорівнює  .
. , але в той же час
, але в той же час  .
. . Тобто довжина дуги M0Mn при зміні х від а до b дорівнює
. Тобто довжина дуги M0Mn при зміні х від а до b дорівнює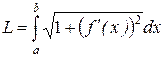 . (7.9)
. (7.9) , що знаходиться між точками
, що знаходиться між точками  і
і  .
.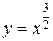 , то
, то  . Тому шукана довжина дуги згідно формулі (7.9) визначається таким чином
. Тому шукана довжина дуги згідно формулі (7.9) визначається таким чином
 .
. =
=
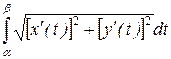 ,
, . (7.10)
. (7.10)

 і
і  . По формулі (7.10) довжина арки циклоїди
. По формулі (7.10) довжина арки циклоїди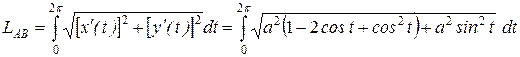 =
=
 .
. . (7.11)
. (7.11) ,
, 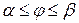 , причому функція
, причому функція  і
і 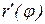 безперервні на відрізку [α, β]. Скористаємося формулами зв'язку між полярними і декартовими координатами
безперервні на відрізку [α, β]. Скористаємося формулами зв'язку між полярними і декартовими координатами  ,
,  , тоді рахуючи кут φ параметром, можна задати рівняння кривої в параметричній формі
, тоді рахуючи кут φ параметром, можна задати рівняння кривої в параметричній формі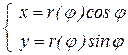

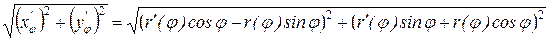 =
=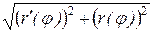 .
. . (7.12)
. (7.12) . Кардіоїда, яка зображена на рисунку
. Кардіоїда, яка зображена на рисунку



 і
і  .
. .
. . (7.13)
. (7.13)
 ), є круг з радіусом у = f(x). Отже, площа поперечного перетину S(x) = π y2.
), є круг з радіусом у = f(x). Отже, площа поперечного перетину S(x) = π y2. . (7.14)
. (7.14)
 =
=  .
.