 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Обчислення визначного інтеграла за допомогою пакету Maxima
Визначний інтеграл integrate(f, x, а, b) де f – підінтегральна функція, x – змінна інтегрування, а і b відповідно верхня і нижня границя інтегрування. Приклади. Обчислити інтеграл: 1) У ячейку введення задаємо команду (%i4) integrate((1+cos(x))^2,x,0,%pi); отримуємо результат (%o4) (3*%pi)/2. 2) (%i14) integrate(cos(2*x)*exp(-х),x,0,3); (%o14) (%e^(-3)*(2*sin(6) -cos(6)))/5+1/5 (%i15) %o14, numer; (%o15) 0.184874675854 Чисельне інтегрування виконується функцією romberg або за допомогою функцій пакету quadpack. Приклад. Обчислити інтеграл У стоці меню вибираємо кнопку Аналіз → Integrate (Рис. 7.2), в результаті виникає допоміжне вікно для введення підінтегральної функції і границь інтегрування Інтегрувати (Рис. 7.3), тут же вказується режим інтегрування (чисельне), а також метод інтегрування romberg або quadpack.
Рис. 7.2
Рис. 7.3 Натискує на клавішу Ok в робочому вікні з‘явиться ячека введення і результат інтегрування (%i2) quad_qags(tan(x)/(sin(x)^2-5*cos(x)^2+4), x %pi/4, acos(1/sqrt(3))); (%o2) [0.081093021621633,9.0031339740762459*10^-16,21,0] У ячейкі виводу (%о2) масив результату обчислення містить: 0.081093021621633 – наближене значення інтеграла; 9.0031339740762459*10^-16 – відносна погрішність обчислень; 21 – число інтервалів розбиття; 0 – ознака коректності обчислень (0 – без проблем). Приклади для самостійного розв‘язання Обчислити визначний інтеграл за допомогою пакету Maxima 1) 4) 7) Застосування визначного інтеграла 7.4.1. Обчислення площ плоских фігур Прямокутні координати Відомо, що визначний інтеграл на відрізку є площа криволінійної трапеції, яка обмежена графіком функції f(x). Якщо графік розташований вищим за вісь Ох (див. рис. 7.4), тобто f(x) > 0,
Рис. 7.4 то площа має знак “+“ і в цьому випадку шукана площа визначається формулою
Якщо графік функції f(x) розташований нижчим за вісь Ох (див. рис. 7.3), тобто f(x) < 0,
Рис. 7.5 то площа має знак “ - ” і Площа фігури, яка обмежена кривими y = f1 (x) і y = f2 (x) (за умовою f2 (x) ≥ f1 (x) див. рис. 7.6), а також прямими x = а і x = b, може бути знайдена за допомогою визначних інтегралів
Рис. 7.6. Приклади. 1. Обчислити площу фігури, яка обмежена графіком функції у = sin x і віссю Ох при
Рис. 7.7. Використовуючи формулу (7.5), знаходимо шукану площу фігури
2. Обчислити площу фігури, яка обмежена лініями у = х, Побудуємо дану фігуру (рис. 7.8)
Рис. 7.8. Знаходимо границі інтегрування : точка перетину ліній у = х,
3. Обчислити площу фігури, яка обмежена лінями Побудуємо фігуру, площу якої необхідно обчислити (рис. 7.9).
Рис. 7.9. Знаходимо точку перетину ліній
Параметричні координати Якщо криволінійна трапеція обмежена кривою, яка задана у параметричній формі
прямими
де α і β визначаються з рівності Приклади. 1. Знайти площу фігури обмеженою еліпсом, який заданий в параметричній формі
Побудуємо фігуру, площу якої необхідно визначити (рис. 7.10)
Рис. 7.10. Знайдемо четверту частину площі S еліпса, яка розташована в першій чверті координатної площини (на рисунку вона зображена сірим кольором). Тут х змінюється від 0 до а , тоді t змінюється від π / 2 до 0. По формулі (7.7) знаходимо
= 2. Обчислити площу фігури, обмеженої однієї аркою циклоїди і віссю Ох. Циклоїда є траєкторія крапки, розташованої на ободі колеса радіусу а, при рівномірному коченні колеса по осі Ох. При одному звороті колеса
Рис. 7.11. Рівняння циклоїди в параметричній формі має вигляд
При зміні
= = Полярні координати В деяких випадках обчислення площ криволінійних фігур зручно проводити в полярних координат. Полярна система координат визначається завданням точки О (полюс) проміння Ор, витікаю чого з точки О (полярній осі) і масштабу для виміру довжини. Положення точки М на площині визначається в полярній системі координат двома числами: полярним радіусом
Рис. 7.12. З рис. 7.12 видно, що незалежно від розміщення точки М на площині мають місце наступні формули переходу: від полярних координат ( від декартових до полярних: Знайдемо площу криволінійного сектора. Хай крива АВ задана в полярних координатах рівнянням
Рис. 7.13. Доведення. Розіб'ємо довільним чином відрізок [α, β] на п частин точками
де Отже, і площа криволінійного сектора чисельно дорівнює цьому визначному інтегралу:
Приклад 1.Обчислити площу фігури, яка обмежена полярною віссю і першим витком спіралі Архімеда:
Мал. 7.12. Розв‘язання. При зміні
Відстань від точки С до полюса рівно Приклад 2.Другий закон Кеплера (закон площ) про рух планет сонячної системи свідчить: площа, що описується радіусом-вектором планети, проведеному з центру Сонця, зростає пропорційно часу. Користуючись цим законом площ, покажемо, що швидкість планети VП в найближчій до Сонця точці орбіти П (перигелій) буде найбільшою, а в найбільш віддаленій від Сонця точці А (афелій) – швидкість буде найменшою (рис. 7.15)
Рис. 7.15. Розглянемо переміщення планети в околицях точок А (афелій) і П (перигелій), за законом Кеплера площі секторів
де З формули для площі криволінійного сектора (7.8) витікає, що
або
Відношення переміщення планети
В результаті
Поиск по сайту: |
 в символьному режимі (аналітично) обчислюється за допомогою команди
в символьному режимі (аналітично) обчислюється за допомогою команди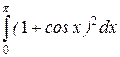



 (
(  ) dx . 2)
) dx . 2) 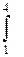 (
( 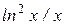 ) dx . 3)
) dx . 3)  ) dx . 5)
) dx . 5)  (
( 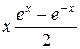 ) dx . 6)
) dx . 6)  (
( 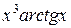 ) dx .
) dx . (
(  ) dx . 8)
) dx . 8)  (
(  ) dx . 9)
) dx . 9) 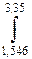 (
(  ) dx . 10)
) dx . 10)  (
(  ) dx. 11)
) dx. 11) 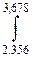 (
( 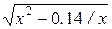 ) dx. 12)
) dx. 12)  (
(  ) dx. 13
) dx. 13  (
(  ) dx. 15)
) dx. 15)  (
(  ) dx .
) dx .
 . (7.5)
. (7.5)
 .
. . (7.6)
. (7.6)
 . Побудуємо дану фігуру (рис. 7.7)
. Побудуємо дану фігуру (рис. 7.7)
 (кв. од.)
(кв. од.) , х = 2 .
, х = 2 .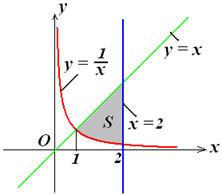
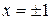 , отже, проміжок інтегрування -
, отже, проміжок інтегрування -  . За формулою (7.6) визначаємо площу фігури
. За формулою (7.6) визначаємо площу фігури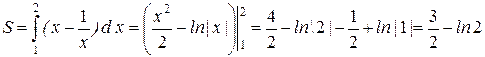 (кв. од.)
(кв. од.)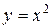 і
і  .
.
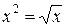 , маємо
, маємо 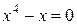 або
або  , звідки
, звідки  . З рисунка видно, що границями інтегрування є
. З рисунка видно, що границями інтегрування є 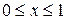 . Визначаємо площу фігури, використовуючи формулу (7.6)
. Визначаємо площу фігури, використовуючи формулу (7.6) (кв. од.)
(кв. од.) ,
, і
і  і віссю Ох, то її площа визначається по формулі
і віссю Ох, то її площа визначається по формулі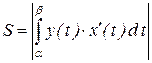 , (7.7)
, (7.7)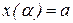 і
і 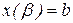 .
. .
.
 =
=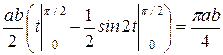 . Таким чином
. Таким чином  . Значить
. Значить 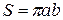 .
. центр колеса переміститься на відстань
центр колеса переміститься на відстань  (рис. 7.11).
(рис. 7.11).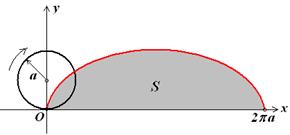
 ,
,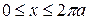 параметр t змінюється в межах
параметр t змінюється в межах 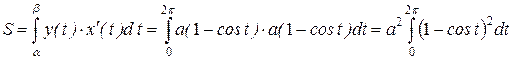 =
= =
=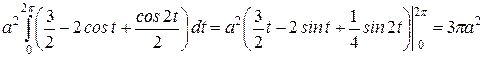 .
.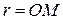 (рис. 7.12), що виражає довжину відрізку ОМ у вибраному масштабі, і полярним кутом φ =
(рис. 7.12), що виражає довжину відрізку ОМ у вибраному масштабі, і полярним кутом φ = 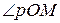 .
.
 ) до декартових (х, у ) :
) до декартових (х, у ) : 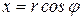 ,
, 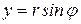 ;
; ,
,  .
. ,
, 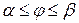 , причому функція
, причому функція  . (7.8)
. (7.8)
 , виберемо на кожному частковому відрізку [
, виберемо на кожному частковому відрізку [  ] довільно точку
] довільно точку 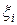 (
(  ) і побудуємо кругові сектори з радіусами
) і побудуємо кругові сектори з радіусами  . В результаті отримаємо віялоподібну фігуру, площа якої приблизно дорівнює площі S криволінійного сектора:
. В результаті отримаємо віялоподібну фігуру, площа якої приблизно дорівнює площі S криволінійного сектора: ,
,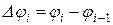 . З іншого боку, площа віялоподібної фігури є інтегральною сумою для інтеграла (7.8). Оскільки функція
. З іншого боку, площа віялоподібної фігури є інтегральною сумою для інтеграла (7.8). Оскільки функція  безперервна на відрізку [α, β], то границя цієї суми при
безперервна на відрізку [α, β], то границя цієї суми при  існує і дорівнює інтегралу (7.8).
існує і дорівнює інтегралу (7.8).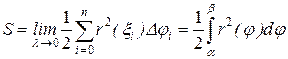 .
.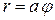 , де а — позитивне число (рис. 7.12).
, де а — позитивне число (рис. 7.12).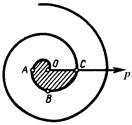
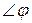 від 0 до 2π полярний радіус описує криву, що обмежує криволінійний сектор ОАВС. Тому по формулі (7.8) маємо
від 0 до 2π полярний радіус описує криву, що обмежує криволінійний сектор ОАВС. Тому по формулі (7.8) маємо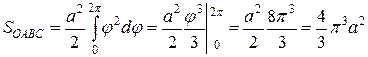 .
. . Тому круг радіусу ОС має площу π ∙OC2 = 4 π3 a2 = 3 ∙
. Тому круг радіусу ОС має площу π ∙OC2 = 4 π3 a2 = 3 ∙ 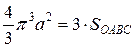 , тобто площа фігури, обмеженою полярною віссю і першим витком спіралі Архімеда, рівна 1/3 площі круга з радіусом, рівним найбільшому з полярних радіусів витка. До цього виводу прийшов ще Архімед.
, тобто площа фігури, обмеженою полярною віссю і першим витком спіралі Архімеда, рівна 1/3 площі круга з радіусом, рівним найбільшому з полярних радіусів витка. До цього виводу прийшов ще Архімед.
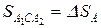 і
і 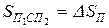 рівні між собою, тобто
рівні між собою, тобто ,
, - площа сектора, що спирається на дугу
- площа сектора, що спирається на дугу  , довжина цієї дуги дорівнює
, довжина цієї дуги дорівнює  , аналогічно
, аналогічно 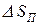 - площа сектора, що спирається на дугу
- площа сектора, що спирається на дугу 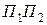 , довжина цієї дуги дорівнює
, довжина цієї дуги дорівнює  .
.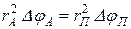
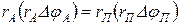 , тобто
, тобто  . Тут
. Тут  і
і  в околиці крапок А і П орбіти. Розділимо попередню рівність на проміжок часу :
в околиці крапок А і П орбіти. Розділимо попередню рівність на проміжок часу :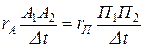 .
. ,
, 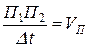 .
. або
або  , звідки витікає, що
, звідки витікає, що .
.