 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Основні властивості визначеного інтеграла
1.Якщо на 2. 3. 4. 5.Якщо на 6.Якщо 7.Якщо точка 8.Якщо функція Теорема (Ньютона-Лейбніца). Якщо функція Формулу (3) називають основною формулою інтегрального числення. Теорема (про заміну змінної у визначеному інтегралі). Нехай функція 1) функція 2) функція 3) Тоді має місце формула:
Як це було і у випадку невизначеного інтеграла, вдалий вибір заміни Нові межі інтегрування Зауваження. Так як визначений інтеграл є число, то при заміні змінних у визначеному інтегралі не треба повертатися до старої змінної, як це було у невизначеному інтегралі. Але при використанні формули (4) треба слідкувати за виконанням умов (1-3) теореми про заміну змінної, інакше можна отримати невірний результат. Теорема(про інтегрування частинами у визначеному інтегралі).Якщо функції Застосування формули (18.5) майже нічим не відрізняється від застосування відповідної формули для визначеного інтеграла. Вибір Іноді спрощення обчислення визначених інтегралів можливо у разі парних, непарних та періодичних функцій. Якщо Якщо Якщо
Поиск по сайту: |
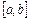 ,
,  ,
, 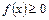 , то
, то  .
.
 ,
,  .
.
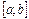
 , то
, то 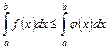 .
. інтегрована на
інтегрована на 
 , то
, то 
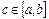 , то
, то 
 така, що
така, що 
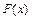 її первісна, то
її первісна, то  .(3)
.(3)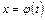 має на
має на  неперервну похідну;
неперервну похідну; та
та  .
. (4)
(4) має першорядне значення для успіху інтегрування. Проведена підстановка доцільна лише тоді, коли обчислення інтеграла після її застосування значно спроститься, порівняно з вихідним інтегралом.
має першорядне значення для успіху інтегрування. Проведена підстановка доцільна лише тоді, коли обчислення інтеграла після її застосування значно спроститься, порівняно з вихідним інтегралом. і
і  знаходимо так. У заміну
знаходимо так. У заміну 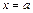 . Дістаємо рівняння
. Дістаємо рівняння  . Його розв’язок і буде новою нижньою межею
. Його розв’язок і буде новою нижньою межею  . Якщо цьому рівнянню задовольняє не одне, а декілька значень
. Якщо цьому рівнянню задовольняє не одне, а декілька значень  , то за
, то за 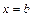 , дістаємо рівняння
, дістаємо рівняння  , його розв’язок і буде новою верхньою межею
, його розв’язок і буде новою верхньою межею  .
. і
і 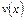 неперервно диференційовні на
неперервно диференційовні на  (5)
(5) і
і  , такий же (див.для невизначеного інтегралу). В якості
, такий же (див.для невизначеного інтегралу). В якості  , та інтегруючи який, знаходимо
, та інтегруючи який, знаходимо  . За
. За  . (6)
. (6) . (7)
. (7) , то
, то  ,
, 