Невизначений інтеграл та його обчислення
Основною задачею інтегрального обчислення є задача обернена до основної задачі диференціального обчислення: за заданою функцією 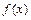 знайти таку функцію знайти таку функцію 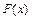 , похідна від якої була б рівною функції , похідна від якої була б рівною функції 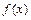 , тобто , тобто 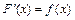 . Таким чином операції диференціювання та інтегрування взаємно обернені. . Таким чином операції диференціювання та інтегрування взаємно обернені.
Означення. Функція 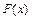 називається первісною для функції називається первісною для функції 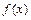 на деякому проміжку на деякому проміжку 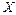 , якщо для кожного , якщо для кожного 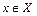 виконується рівність виконується рівність
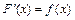 (1) (1)
Процес знаходження первісної функції 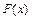 для заданої функції називається інтегруванням функції. Будь-яка неперервна функція має первісну. Якщо для заданої функції називається інтегруванням функції. Будь-яка неперервна функція має первісну. Якщо 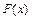 первісна для функції первісна для функції 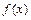 на проміжку на проміжку 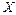 , то будь-яка інша первісна для , то будь-яка інша первісна для 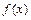 на на 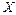 може бути представлена у вигляді може бути представлена у вигляді  , де , де  - довільна постійна. - довільна постійна.
Означення. Якщо функція 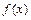 має первісну має первісну 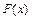 , то множина всіх первісних цієї функції , то множина всіх первісних цієї функції  , де , де  - довільна постійна, називається невизначеним інтегралом від - довільна постійна, називається невизначеним інтегралом від 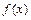 і позначається символом і позначається символом
 , ,  (2) (2)
При цьому називають: 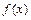 - підінтегральна функція, - підінтегральна функція,  - підінтегральний вираз, - підінтегральний вираз,  - змінна інтегрування. - змінна інтегрування.
Властивості невизначеного інтеграла:
1. 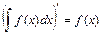 ; ;
2.  ; ;
3.  ; ;
4.  , , 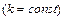 ; ;
5. 
 . .
Наслідок:

 . .
Таблиця основних інтегралів
Єдиного алгоритму для знаходження невизначених інтегралів у скінченному вигляді (через елементарні функції) не існує. Основні формули інтегрування, записані нижче, можна дістати шляхом обернення формул для похідних основних елементарних функцій. Подаємо основні табличні інтеграли, покладаючи, що 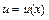 - складна неперервна функція і - складна неперервна функція і  . .
1.  ; ;  ; ;
2. 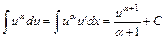 , ,  ; ;  ; ;
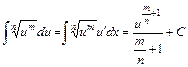 ; ;  ; ;
3.  ; ;
4.  ; ; 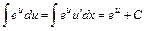 ; ;
5.  ; ;
6.  ; ;
7. 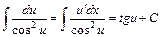 ; ;
8. 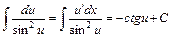 ; ;
9.  ; ;
10. 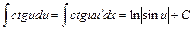 ; ;
11.  ; ;
12. 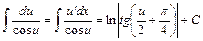 ; ;
13. 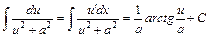 ; ;
14.  ; ;
15.  ; ;
16.  ; ;
17.  ; ;
18.  ; ;
19.  ; ;
20. 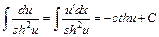 . .
Майстерність інтегрування полягає в умінні так перетворити підінтегральний вираз, щоб останній став одним із табличних. Загальний алгоритм знаходження невизначених інтегралів:
1) перетворити підінтегральний вираз з вище указаною метою;
2) розкласти інтеграл від алгебраїчної суми функцій на алгебраїчну суму інтегралів від цих функцій;
3) винести постійний множник за знак інтеграла;
4) застосувати відповідні табличні інтеграли. (Коли немає необхідності в застосуванні якоїсь із перерахованих операцій, вона опускається).
Наведемо приклади табличного інтегрування.
Приклад 1
Обчислити інтеграли:
1) 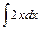 ; 2) ; 2)  ; 3) ; 3)  ; ;
4)  ; 5) ; 5) 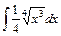 ; 6) ; 6)  ; ;
7)  8) 8) 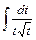 ; 9) ; 9)  ; 10) ; 10)  . .
Розв’язання
1) За властивістю 4 невизначеного інтеграла і табличним інтегралом (2) знаходимо
 . .
2) Аналогічно попередньому маємо
 . .
3)  . .
4) За властивістю 4 невизначеного інтеграла, табличним інтегралом (2) та враховуючи, що  , дістаємо , дістаємо  . .
5) Аналогічно 4), враховуючи що  , знаходимо , знаходимо
 . .
6) Аналогічно 4), враховуючи що  , маємо , маємо
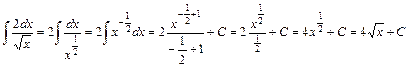 . .
7) 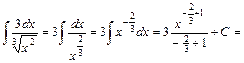 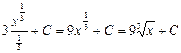 . .
8) Аналогічно попередньому, зважаючи що  , дістаємо , дістаємо
  . .
9)  
 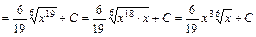 . .
10) 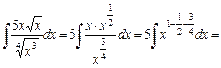 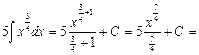  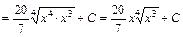 . .
Приклад 2
Обчислити інтеграли
1) 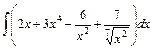 ; 2) ; 2)  ; 3) ; 3)  ; ;
Розв’язання
1) Використовуємо наслідок 4-ї та 5-ї властивості невизначеного інтеграла та досвід розв’язування прикладу 1.
    . .
2) Аналогічно попередньому, враховуючи що  , дістаємо , дістаємо
 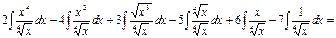
    
 . .
3) Розв’язуємо аналогічно пр.1, попередньо спростивши підінтегральний вираз, розкривши куб різниці за формулою 
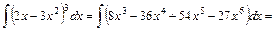 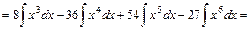
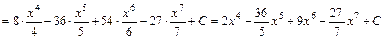 . .
Приклад 3
Обчислити інтеграли:
1)  ; 2) ; 2) 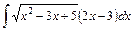 ; 3) ; 3) 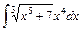 ; 4) ; 4)  ; ;
5)  ; 6) ; 6)  ; 7) ; 7)  . .
Розв’язання
При обчисленні цих інтегралів будемо користуватися табличним інтегралом (2) 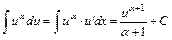 . Перед обчисленням кожного інтеграла для себе треба з’ясувати наступне: . Перед обчисленням кожного інтеграла для себе треба з’ясувати наступне:
1) яку із функцій, котрі стоять під знаком інтеграла, треба прийняти за  ; ;
2) чи стоїть за нею множник рівний  , тобто чи стоїть під знаком інтеграла , тобто чи стоїть під знаком інтеграла  ; ;
3) коли це так, то, формулу (2) використовуємо зразу ж. Якщо ж підінтегральна функція не має вигляду  , але відрізняється від неї лише на деякий постійний множник , але відрізняється від неї лише на деякий постійний множник 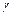 , то помноживши і розділивши підінтегральну функцію на множник , то помноживши і розділивши підінтегральну функцію на множник 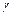 та виносячи множник та виносячи множник  за знак інтеграла, дістанемо табличну підінтегральну функцію за знак інтеграла, дістанемо табличну підінтегральну функцію  і можемо використовувати формулу (2). і можемо використовувати формулу (2).
1) 
Будемо користуватися табличним інтегралом (2). Для цього покладемо    , ,  . Тоді підінтегральна функція має табличний вигляд . Тоді підінтегральна функція має табличний вигляд 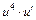 і табличним інтегралом (2) можна зразу користуватися і табличним інтегралом (2) можна зразу користуватися
 . .
2) 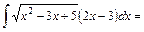
Покладемо  . .
Тоді, зважаючи що  підінтегральна функція має табличний вигляд підінтегральна функція має табличний вигляд  і табличним інтегралом (2) можна користуватися. і табличним інтегралом (2) можна користуватися.

  . .
3) 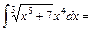
Покладемо  і і  . Щоб дістати табличну підінтегральну функцію множимо та ділимо підінтегральний вираз на 5 та виносимо . Щоб дістати табличну підінтегральну функцію множимо та ділимо підінтегральний вираз на 5 та виносимо  за знак інтеграла. за знак інтеграла.
  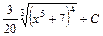 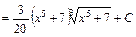 . .
4) 
Виберемо
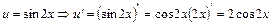 ; ;  . .
Для того, щоб підінтегральна функція стала табличною  множимо та ділимо підінтегральний вираз на 2 і виносимо множник множимо та ділимо підінтегральний вираз на 2 і виносимо множник  за знак інтеграла. за знак інтеграла.
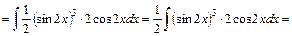  . .
5) 
Перетворимо цей інтеграл до табличного (2):
 . .
Тоді
   ; ;  . .
Множимо та ділимо підінтегральний вираз на (-3) і виносимо 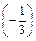 за знак інтеграла. Дістаємо табличний інтеграл (2). за знак інтеграла. Дістаємо табличний інтеграл (2).


 . .
6) 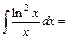
Покладемо  і і  , ,  . Підінтегральна функція зразу є табличною . Підінтегральна функція зразу є табличною  . .
 . .
7) 
Перетворимо цей підінтегральний вираз до табличного (2), зважаючи що  . .
Тоді  ; ;  . Множимо та ділимо підінтегральний вираз на (-2) та виносимо . Множимо та ділимо підінтегральний вираз на (-2) та виносимо  за знак інтеграла. Дістаємо табличний інтеграл (2). за знак інтеграла. Дістаємо табличний інтеграл (2).

 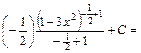  . .
Приклад 4
Обчислити інтеграли, користуючись табличним інтегралом (3):
1)  ; 2) ; 2)  ; 3) ; 3)  ; 4) ; 4)  ; 5) ; 5)  . .
Розв’язання
Відзначимо, що при використанні табличного інтеграла (3)  підінтегральна функція повинна мати вигляд підінтегральна функція повинна мати вигляд  , інакше інтегралом (3) не можна користуватися. У тих випадках, коли підінтегральна функція обчислювального інтегралу відрізняється від , інакше інтегралом (3) не можна користуватися. У тих випадках, коли підінтегральна функція обчислювального інтегралу відрізняється від  лише на деякий постійний множник лише на деякий постійний множник 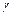 , то помноживши та розділивши підінтегральну функцію на , то помноживши та розділивши підінтегральну функцію на 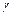 і виносячи постійний множник і виносячи постійний множник  за знак інтеграла, дістаємо табличний інтеграл (3). за знак інтеграла, дістаємо табличний інтеграл (3).
1) 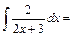
Покладемо  . Очевидно підінтегральна функція має вигляд . Очевидно підінтегральна функція має вигляд  і табличним інтегралом (3) можна користуватися. Тому і табличним інтегралом (3) можна користуватися. Тому 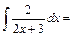 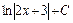 . .
2) 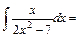
Покладемо  . Множимо та ділимо підінтегральну функцію на 4, виносимо . Множимо та ділимо підінтегральну функцію на 4, виносимо 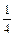 за знак інтеграла. Тепер табличним інтегралом (3) можна користуватися. за знак інтеграла. Тепер табличним інтегралом (3) можна користуватися.
 . .
3) 
Покладемо  . Множимо та ділимо підінтегральну функцію на (-2) і виносимо . Множимо та ділимо підінтегральну функцію на (-2) і виносимо  за знак інтеграла. Дістаємо табличний інтеграл (3). за знак інтеграла. Дістаємо табличний інтеграл (3).
 . .
4) 
Покладемо  . Множимо та ділимо підінтегральний вираз на 20 та виносимо . Множимо та ділимо підінтегральний вираз на 20 та виносимо 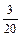 за знак інтеграла. Дістаємо табличний інтеграл (3). за знак інтеграла. Дістаємо табличний інтеграл (3).
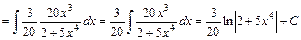 . .
5) 
Покладемо 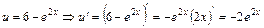 . .
Множимо та ділимо підінтегральну функцію на (-2) та виносимо  за знак інтеграла. Дістаємо табличний інтеграл (3). за знак інтеграла. Дістаємо табличний інтеграл (3).
 . .
Приклад 5
Обчислити інтеграли від показникових функцій:
1) 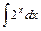 ; 2) ; 2) 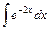 ; 3) ; 3)  ; 4) ; 4)  ; ;
5) 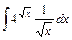 ; 6) ; 6)  ; 7) ; 7)  ; 8) ; 8) 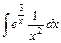 . .
Розв’язання
Використовуємо табличний інтеграл (4)
 , , 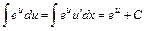 (4) (4)
Звернемо увагу на те, що підінтегральні функції в обох інтегралах являють собою добутки  та та  . Якщо множники . Якщо множники  в підінтегральних формулах відсутні, користуватись формулами (4) не можна. Якщо ж підінтегральні функції відрізняються від в підінтегральних формулах відсутні, користуватись формулами (4) не можна. Якщо ж підінтегральні функції відрізняються від  та та  лише постійним множником лише постійним множником 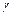 , то помноживши і розділивши їх на , то помноживши і розділивши їх на 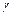 та винісши множник та винісши множник  під знак інтеграла, дістаємо табличний підінтегральний вираз і тепер використовувати формули (4) можливо. У частинному випадку, якщо під знак інтеграла, дістаємо табличний підінтегральний вираз і тепер використовувати формули (4) можливо. У частинному випадку, якщо  - аргумент та - аргумент та  , формули (4) мають вигляд , формули (4) мають вигляд
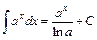 , , 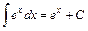 ( ( 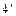 ) )
1)  ; ;
2) 

 ; ;
3) 

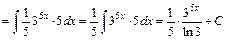 ; ;
4) 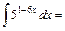
  ; ;
5) 
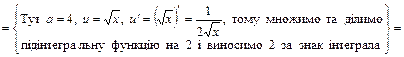
 ; ;
6) 

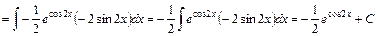 ; ;
7)  
 ; ;
8) 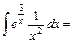 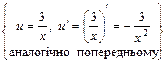
  . .
Приклад 6
Користуючись табличними інтегралами (5-12), обчислити інтеграли від тригонометричних функцій:
1)  ; 2) ; 2)  ; 3) ; 3)  ; 4) ; 4)  ; ;
5)  ; 6) ; 6)  ; 7) ; 7)  ; 8) ; 8)  . .
Розв’язання
Слід звернути увагу на те, що кожна з підінтегральних функцій табличних інтегралів (5-12) має множник  і в разі його відсутності користування формулами (5-12) неможливо. Якщо ж розглядувані підінтегральні функції відрізняються від табличних (5-12) лише на постійний множник і в разі його відсутності користування формулами (5-12) неможливо. Якщо ж розглядувані підінтегральні функції відрізняються від табличних (5-12) лише на постійний множник 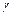 , то помноживши і розділивши їх на , то помноживши і розділивши їх на 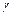 та виносячи множник та виносячи множник  за знак інтеграла, дістанемо табличні підінтегральні вирази і право користуватися табличними формулами. У частинному випадку, коли за знак інтеграла, дістанемо табличні підінтегральні вирази і право користуватися табличними формулами. У частинному випадку, коли 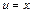   формули (5-12) матимуть вигляд: формули (5-12) матимуть вигляд:
 ; ; 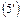
 ; ; 
 ; ; 
 ; ; 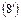
 ; ; 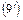
 ; ; 
 ; ; 
 
1) 
Використаємо формулу (5) Підінтегральна функція повинна мати вигляд  .Тому покладемо .Тому покладемо    . Множимо і ділимо підінтегральні вирази на 3 та виносимо постійний множник . Множимо і ділимо підінтегральні вирази на 3 та виносимо постійний множник 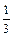 за знак інтеграла. за знак інтеграла.
=  = =  . .
2) 
Використаємо формулу (6) підінтегральна функція повинна мати вигляд  . .
Тому покладемо    . Виносимо множник 4 за знак інтеграла і дістаємо табличний інтеграл (6). . Виносимо множник 4 за знак інтеграла і дістаємо табличний інтеграл (6).
=  . .
3) 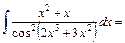
Використовуємо формулу (7). Підінтегральна функція повинна мати вигляд  . .
Тому покладемо    . Множимо та ділимо підінтегральний вираз на 6 та виносимо . Множимо та ділимо підінтегральний вираз на 6 та виносимо  за знак інтеграла. Дістаємо табличний інтеграл (7). за знак інтеграла. Дістаємо табличний інтеграл (7).
=  . .
4) 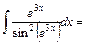
Користуємось формулою (8). Підінтегральна функція повинна мати вигляд  . Тому покладемо . Тому покладемо 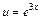   . Множимо та ділимо підінтегральний вираз на 3 та виносимо . Множимо та ділимо підінтегральний вираз на 3 та виносимо 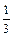 за знак інтеграла. за знак інтеграла.
 . .
5) 
Вибираємо формулу (9).Підінтегральна функція повинна мати вигляд  .Тому покладемо .Тому покладемо    . Множимо та ділимо підінтегральний вираз на 8, виносимо . Множимо та ділимо підінтегральний вираз на 8, виносимо  за знак інтеграла і отримаємо табличний інтеграл (9) за знак інтеграла і отримаємо табличний інтеграл (9)
  . .
6) 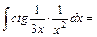
Вибираємо формулу (10). Підінтегральна функція повинна мати вигляд 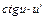 . .
Тому покладемо 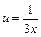  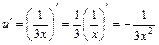 . Множимо та ділимо підінтегральний вираз на . Множимо та ділимо підінтегральний вираз на 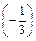 , виносимо , виносимо  за знак інтеграла і дістаємо табличний інтеграл (10). за знак інтеграла і дістаємо табличний інтеграл (10).
 . .
7) 
Будемо користуватися табличним інтегралом (12). Підінтегральна функція повинна мати вигляд  ,тому покладемо ,тому покладемо    . Множимо та ділимо підінтегральний вираз на 7 та виносимо множник . Множимо та ділимо підінтегральний вираз на 7 та виносимо множник  за знак інтеграла. Дістаємо табличний інтеграл (12). за знак інтеграла. Дістаємо табличний інтеграл (12).
 . .
8)  = =
Використовуємо табличний інтеграл (11) в якому підінтегральна функція має вигляд  . .
Виходячи с цього, покладемо    . Множимо та ділимо підінтегральний вираз на . Множимо та ділимо підінтегральний вираз на 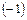 , виносимо , виносимо 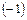 за знак інтеграла і отримуємо табличний інтеграл (11). за знак інтеграла і отримуємо табличний інтеграл (11).
 . .
Приклад 7
Обчислити інтеграли користуючись формулами (13-16):
1)  ; 2) ; 2)   ; 3) ; 3)  ; ;
4)  ; 5) ; 5)  ; 6) ; 6)  ; ;
7)  ; 8) ; 8)  ; 9) ; 9)  ; ;
10)  ; 11) ; 11) 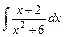 ; 12) ; 12)  . .
Розв’язання
Формули (13-18) мають відповідно підінтегральні функції  (13); (13); 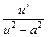 (14); (14);  (15); (15); 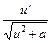 (16). Якщо в конкретних інтегралах, зробивши тотожні перетворення, можна виділити такі підінтегральні функції, то відповідні інтеграли можна застосовувати для обчислень. У частинному випадку, коли (16). Якщо в конкретних інтегралах, зробивши тотожні перетворення, можна виділити такі підінтегральні функції, то відповідні інтеграли можна застосовувати для обчислень. У частинному випадку, коли 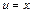   , формули (13-16) приймають вигляд: , формули (13-16) приймають вигляд:
 , ( , ( 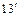 ) )
 , ( , (  ) )
 , ( , (  ) )
 . ( . ( 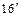 ) )
1) 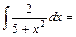
Користуємось властивістю (4) невизначеного інтеграла та табличним інтегралом (13'). У цьому прикладі    . Тому . Тому
 . .
2) 
Використаємо табличний інтеграл (13). Покладемо   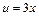   ; ; 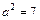   . Множимо та ділимо підінтегральну функцію на 3, виносимо множник . Множимо та ділимо підінтегральну функцію на 3, виносимо множник 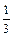 за знак інтеграла і дістаємо підінтегральну функцію інтеграла (13). за знак інтеграла і дістаємо підінтегральну функцію інтеграла (13).

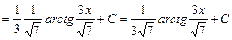 . .
3) 
Використаємо табличний інтеграл (13). Покладемо   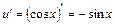 ; ;    . Множимо та ділимо підінтегральну функцію на (-1) та виносимо (-5) за знак інтеграла. Дістаємо табличний інтеграл (13). . Множимо та ділимо підінтегральну функцію на (-1) та виносимо (-5) за знак інтеграла. Дістаємо табличний інтеграл (13).

 . .
4) 
Використаємо табличний інтеграл  . Покладемо . Покладемо    та виносимо множник та виносимо множник  за знак інтеграла. Дістаємо табличний інтеграл за знак інтеграла. Дістаємо табличний інтеграл  . .
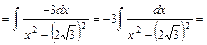
 . .
5) 
Використаємо табличний інтеграл (14), покладаючи      ; ; 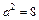  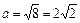 . Множимо та ділимо підінтегральну функцію на . Множимо та ділимо підінтегральну функцію на  та виносимо множник та виносимо множник 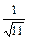 за знак інтеграла. Дістаємо табличний інтеграл (14). за знак інтеграла. Дістаємо табличний інтеграл (14).

 . .
6) 
Використаємо табличний інтеграл (14). Покладемо    ; ;  . Множимо та ділимо підінтегральну функцію на 2 та виносимо множник . Множимо та ділимо підінтегральну функцію на 2 та виносимо множник 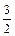 за знак інтеграла. Дістаємо табличний інтеграл (14). за знак інтеграла. Дістаємо табличний інтеграл (14).

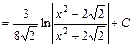 . .
7) 
Використаємо табличний інтеграл (16). Тут  , маємо зразу табличний інтеграл , маємо зразу табличний інтеграл  . .
 . .
8) 
Використаємо табличний інтеграл (16), покладаючи    ; ;  . Множимо та ділимо підінтегральну функцію на 3, виносимо множник . Множимо та ділимо підінтегральну функцію на 3, виносимо множник 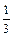 за знак інтеграла. Дістаємо табличний інтеграл (16). за знак інтеграла. Дістаємо табличний інтеграл (16).
 . .
9) 
Використаємо табличний інтеграл (15). Покладемо    ; ;     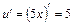 . Множимо та ділимо підінтегральну функцію на 5, виносимо множник . Множимо та ділимо підінтегральну функцію на 5, виносимо множник  за знак інтеграла. Дістаємо табличний інтеграл (15). за знак інтеграла. Дістаємо табличний інтеграл (15).
 . .
10) 
Використаємо табличний інтеграл (15). Покладемо    ; ;   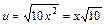   . Множимо та ділимо підінтегральну функцію на . Множимо та ділимо підінтегральну функцію на  , виносимо множник , виносимо множник  за знак інтеграла, та дістаємо табличний інтеграл. за знак інтеграла, та дістаємо табличний інтеграл.
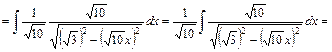
 . .
11) 
Зведемо обчислення до табличних інтегралів (3) та (13), зважаючи на те, що  та використовуючи властивості (5) та (4) невизначених інтегралів. та використовуючи властивості (5) та (4) невизначених інтегралів.
 
 . .
12) 
Зведемо обчислення до табличних інтегралів (3) та (14), діючи аналогічно прикладу 11.
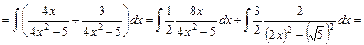
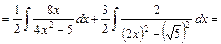 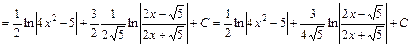 . .
Завдання для самостійної роботи:
Обчислити інтеграли:
1) 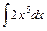 ; 2) ; 2)  ; 3) ; 3)  ; 4) ; 4)  ; ;
5)  ; 6) ; 6)  ; 7) ; 7)  ; 8) ; 8)  ; ;
9)  ; 10) ; 10)  ; 11) ; 11)  ; 12) ; 12)  ; ;
13)  14) 14)  ; 15) ; 15)  ; 16) ; 16)  ; ;
17)  ; 18) ; 18)  ; 19) ; 19)  ; 20) ; 20)  ; ;
21)  ; 22) ; 22)  ; 23) ; 23)  ; 24) ; 24)  ; ;
25)  ; 26) ; 26)  ; 27) ; 27)  ; 28) ; 28)  ; ;
29)  ; 30) ; 30) 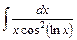 ; 31) ; 31)  ; 32) ; 32) 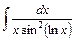 ; ;
33)  ; 34) ; 34)  ; 35) ; 35)  ; 36) ; 36) 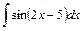 ; ;
37) 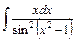 ; 38) ; 38)  ; 39) ; 39)  ; 40) ; 40) 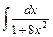 ; ;
41)  ; 42) ; 42)  ; 43) ; 43)  ; 44) ; 44)  ; ;
45)  ; 46) ; 46)  ; 47) ; 47) 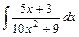 ; 48) ; 48)  ; ;
49)  ; 50) ; 50)  ; 51) ; 51)  ; 52) ; 52)  . .
Відповіді:
1)  ; 2) ; 2)  ; ;
3)  ; 4) ; 4)  ; ;
5)  ; 6) ; 6)  ; ;
7) 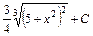 ; 8) ; 8)  ; ;
9) 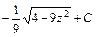 ; 10) ; 10) 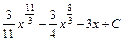 ; ;
11) 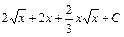 ; 12) ; 12)  ; ;
13)  ; 14) ; 14)  ; ;
15)  ; 16) ; 16)  ; ;
17)  ; 18) ; 18)  ; ;
19)  ; 20) ; 20)  ; ;
21)  ; 22) ; 22)  ; ;
Поиск по сайту:
|

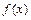 знайти таку функцію
знайти таку функцію 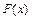 , похідна від якої була б рівною функції
, похідна від якої була б рівною функції 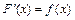 . Таким чином операції диференціювання та інтегрування взаємно обернені.
. Таким чином операції диференціювання та інтегрування взаємно обернені.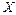 , якщо для кожного
, якщо для кожного 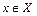 виконується рівність
виконується рівність , де
, де  - довільна постійна.
- довільна постійна. ,
,  (2)
(2) - підінтегральний вираз,
- підінтегральний вираз,  - змінна інтегрування.
- змінна інтегрування.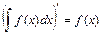 ;
; ;
; ;
; ,
, 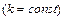 ;
;
 .
.
 .
.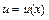 - складна неперервна функція і
- складна неперервна функція і  .
. ;
;  ;
;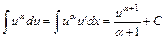 ,
,  ;
;  ;
;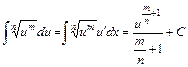 ;
;  ;
; ;
; ;
; 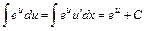 ;
; ;
; ;
;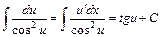 ;
;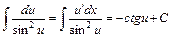 ;
; ;
;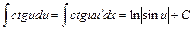 ;
; ;
;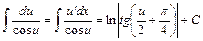 ;
;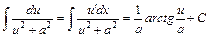 ;
; ;
; ;
; ;
; ;
; ;
; ;
;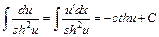 .
.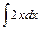 ; 2)
; 2)  ; 3)
; 3)  ;
; ; 5)
; 5) 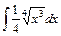 ; 6)
; 6)  ;
; 8)
8) 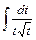 ; 9)
; 9)  ; 10)
; 10)  .
. .
. .
. .
. , дістаємо
, дістаємо  .
. , знаходимо
, знаходимо .
. , маємо
, маємо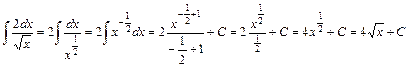 .
.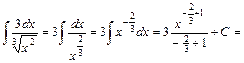
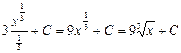 .
. , дістаємо
, дістаємо
 .
.


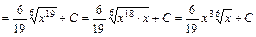 .
.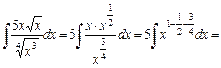
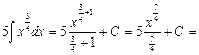

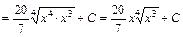 .
.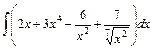 ; 2)
; 2)  ; 3)
; 3)  ;
;


 .
. , дістаємо
, дістаємо
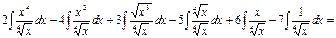





 .
.
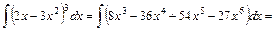
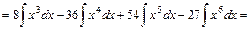
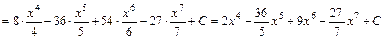 .
. ; 2)
; 2) 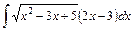 ; 3)
; 3) 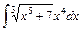 ; 4)
; 4)  ;
; ; 6)
; 6)  ; 7)
; 7)  .
.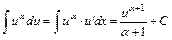 . Перед обчисленням кожного інтеграла для себе треба з’ясувати наступне:
. Перед обчисленням кожного інтеграла для себе треба з’ясувати наступне: ;
; , тобто чи стоїть під знаком інтеграла
, тобто чи стоїть під знаком інтеграла  ;
;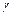 , то помноживши і розділивши підінтегральну функцію на множник
, то помноживши і розділивши підінтегральну функцію на множник  за знак інтеграла, дістанемо табличну підінтегральну функцію
за знак інтеграла, дістанемо табличну підінтегральну функцію 


 ,
,  . Тоді підінтегральна функція має табличний вигляд
. Тоді підінтегральна функція має табличний вигляд 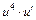 і табличним інтегралом (2) можна зразу користуватися
і табличним інтегралом (2) можна зразу користуватися .
.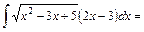
 .
. підінтегральна функція має табличний вигляд
підінтегральна функція має табличний вигляд  і табличним інтегралом (2) можна користуватися.
і табличним інтегралом (2) можна користуватися.

 .
.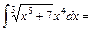
 і
і  . Щоб дістати табличну підінтегральну функцію множимо та ділимо підінтегральний вираз на 5 та виносимо
. Щоб дістати табличну підінтегральну функцію множимо та ділимо підінтегральний вираз на 5 та виносимо  за знак інтеграла.
за знак інтеграла.

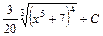
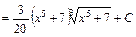 .
.
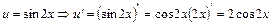 ;
;  .
. множимо та ділимо підінтегральний вираз на 2 і виносимо множник
множимо та ділимо підінтегральний вираз на 2 і виносимо множник  за знак інтеграла.
за знак інтеграла.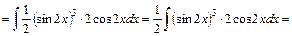
 .
.
 .
.
 ;
;  .
.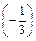 за знак інтеграла. Дістаємо табличний інтеграл (2).
за знак інтеграла. Дістаємо табличний інтеграл (2).

 .
.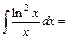
 і
і  ,
, 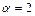 . Підінтегральна функція зразу є табличною
. Підінтегральна функція зразу є табличною  .
. .
.
 .
. ;
;  . Множимо та ділимо підінтегральний вираз на (-2) та виносимо
. Множимо та ділимо підінтегральний вираз на (-2) та виносимо  за знак інтеграла. Дістаємо табличний інтеграл (2).
за знак інтеграла. Дістаємо табличний інтеграл (2).

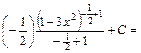
 .
. ; 2)
; 2)  ; 3)
; 3)  ; 4)
; 4)  ; 5)
; 5)  .
. підінтегральна функція повинна мати вигляд
підінтегральна функція повинна мати вигляд  , інакше інтегралом (3) не можна користуватися. У тих випадках, коли підінтегральна функція обчислювального інтегралу відрізняється від
, інакше інтегралом (3) не можна користуватися. У тих випадках, коли підінтегральна функція обчислювального інтегралу відрізняється від 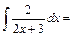
 . Очевидно підінтегральна функція має вигляд
. Очевидно підінтегральна функція має вигляд 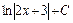 .
.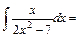
 . Множимо та ділимо підінтегральну функцію на 4, виносимо
. Множимо та ділимо підінтегральну функцію на 4, виносимо 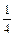 за знак інтеграла. Тепер табличним інтегралом (3) можна користуватися.
за знак інтеграла. Тепер табличним інтегралом (3) можна користуватися. .
.
 . Множимо та ділимо підінтегральну функцію на (-2) і виносимо
. Множимо та ділимо підінтегральну функцію на (-2) і виносимо  .
.
 . Множимо та ділимо підінтегральний вираз на 20 та виносимо
. Множимо та ділимо підінтегральний вираз на 20 та виносимо 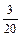 за знак інтеграла. Дістаємо табличний інтеграл (3).
за знак інтеграла. Дістаємо табличний інтеграл (3).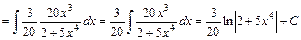 .
.
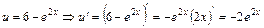 .
. .
.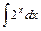 ; 2)
; 2) 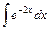 ; 3)
; 3)  ; 4)
; 4)  ;
;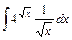 ; 6)
; 6)  ; 7)
; 7)  ; 8)
; 8) 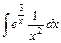 .
. ,
,  та
та  . Якщо множники
. Якщо множники  , формули (4) мають вигляд
, формули (4) мають вигляд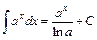 ,
, 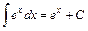 (
(  )
) ;
;

 ;
;

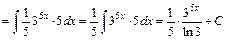 ;
;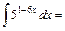

 ;
;
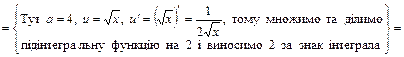
 ;
;

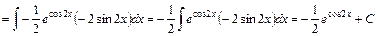 ;
;

 ;
;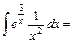
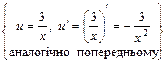

 .
. ; 2)
; 2)  ; 3)
; 3)  ; 4)
; 4)  ;
; ; 6)
; 6)  ; 7)
; 7)  ; 8)
; 8)  .
.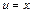
 формули (5-12) матимуть вигляд:
формули (5-12) матимуть вигляд: ;
; 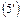
 ;
; 
 ;
; 
 ;
; 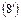
 ;
; 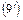
 ;
; 
 ;
; 



 .Тому покладемо
.Тому покладемо 
 . Множимо і ділимо підінтегральні вирази на 3 та виносимо постійний множник
. Множимо і ділимо підінтегральні вирази на 3 та виносимо постійний множник 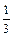 за знак інтеграла.
за знак інтеграла. =
=  .
.
 .
.
 . Виносимо множник 4 за знак інтеграла і дістаємо табличний інтеграл (6).
. Виносимо множник 4 за знак інтеграла і дістаємо табличний інтеграл (6). .
.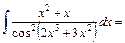
 .
.
 . Множимо та ділимо підінтегральний вираз на 6 та виносимо
. Множимо та ділимо підінтегральний вираз на 6 та виносимо  за знак інтеграла. Дістаємо табличний інтеграл (7).
за знак інтеграла. Дістаємо табличний інтеграл (7). .
.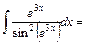
 . Тому покладемо
. Тому покладемо 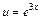
 . Множимо та ділимо підінтегральний вираз на 3 та виносимо
. Множимо та ділимо підінтегральний вираз на 3 та виносимо  .
.
 .Тому покладемо
.Тому покладемо 
 . Множимо та ділимо підінтегральний вираз на 8, виносимо
. Множимо та ділимо підінтегральний вираз на 8, виносимо  за знак інтеграла і отримаємо табличний інтеграл (9)
за знак інтеграла і отримаємо табличний інтеграл (9)
 .
.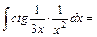
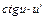 .
.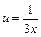
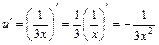 . Множимо та ділимо підінтегральний вираз на
. Множимо та ділимо підінтегральний вираз на  за знак інтеграла і дістаємо табличний інтеграл (10).
за знак інтеграла і дістаємо табличний інтеграл (10). .
.
 ,тому покладемо
,тому покладемо 
 . Множимо та ділимо підінтегральний вираз на 7 та виносимо множник
. Множимо та ділимо підінтегральний вираз на 7 та виносимо множник  за знак інтеграла. Дістаємо табличний інтеграл (12).
за знак інтеграла. Дістаємо табличний інтеграл (12). .
. .
.
 . Множимо та ділимо підінтегральний вираз на
. Множимо та ділимо підінтегральний вираз на 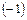 , виносимо
, виносимо  .
. ; 2)
; 2) 
 ; 3)
; 3)  ;
; ; 5)
; 5)  ; 6)
; 6)  ;
; ; 8)
; 8)  ; 9)
; 9)  ;
; ; 11)
; 11) 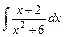 ; 12)
; 12)  .
. (13);
(13); 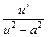 (14);
(14);  (15);
(15); 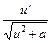 (16). Якщо в конкретних інтегралах, зробивши тотожні перетворення, можна виділити такі підінтегральні функції, то відповідні інтеграли можна застосовувати для обчислень. У частинному випадку, коли
(16). Якщо в конкретних інтегралах, зробивши тотожні перетворення, можна виділити такі підінтегральні функції, то відповідні інтеграли можна застосовувати для обчислень. У частинному випадку, коли  , (
, ( 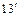 )
) , (
, (  )
) , (
, (  )
) . (
. ( 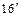 )
)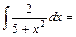

 . Тому
. Тому .
.

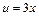
 ;
; 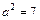
 . Множимо та ділимо підінтегральну функцію на 3, виносимо множник
. Множимо та ділимо підінтегральну функцію на 3, виносимо множник 
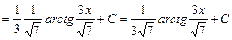 .
.

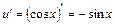 ;
; 
 . Множимо та ділимо підінтегральну функцію на (-1) та виносимо (-5) за знак інтеграла. Дістаємо табличний інтеграл (13).
. Множимо та ділимо підінтегральну функцію на (-1) та виносимо (-5) за знак інтеграла. Дістаємо табличний інтеграл (13).
 .
.
 . Покладемо
. Покладемо 
 та виносимо множник
та виносимо множник 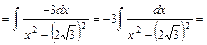
 .
.


 ;
; 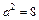
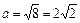 . Множимо та ділимо підінтегральну функцію на
. Множимо та ділимо підінтегральну функцію на  та виносимо множник
та виносимо множник 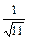 за знак інтеграла. Дістаємо табличний інтеграл (14).
за знак інтеграла. Дістаємо табличний інтеграл (14).
 .
.


 ;
;  . Множимо та ділимо підінтегральну функцію на 2 та виносимо множник
. Множимо та ділимо підінтегральну функцію на 2 та виносимо множник 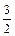 за знак інтеграла. Дістаємо табличний інтеграл (14).
за знак інтеграла. Дістаємо табличний інтеграл (14).
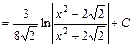 .
.
 , маємо зразу табличний інтеграл
, маємо зразу табличний інтеграл  .
. .
.


 . Множимо та ділимо підінтегральну функцію на 3, виносимо множник
. Множимо та ділимо підінтегральну функцію на 3, виносимо множник  .
.
 ;
; 

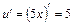 . Множимо та ділимо підінтегральну функцію на 5, виносимо множник
. Множимо та ділимо підінтегральну функцію на 5, виносимо множник  .
.

 ;
; 
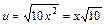
 . Множимо та ділимо підінтегральну функцію на
. Множимо та ділимо підінтегральну функцію на  , виносимо множник
, виносимо множник  за знак інтеграла, та дістаємо табличний інтеграл.
за знак інтеграла, та дістаємо табличний інтеграл.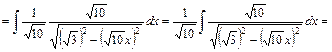
 .
.
 та використовуючи властивості (5) та (4) невизначених інтегралів.
та використовуючи властивості (5) та (4) невизначених інтегралів.

 .
.
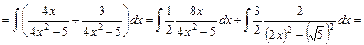
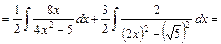
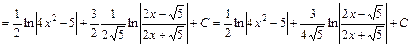 .
.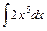 ; 2)
; 2)  ; 3)
; 3)  ; 4)
; 4)  ;
; ; 6)
; 6)  ; 7)
; 7)  ; 8)
; 8)  ;
; ; 10)
; 10)  ; 11)
; 11)  ; 12)
; 12)  ;
; 14)
14)  ; 15)
; 15)  ; 16)
; 16)  ;
; ; 18)
; 18)  ; 19)
; 19)  ; 20)
; 20)  ;
; ; 22)
; 22)  ; 23)
; 23)  ; 24)
; 24)  ;
; ; 26)
; 26)  ; 27)
; 27)  ; 28)
; 28)  ;
; ; 30)
; 30) 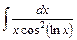 ; 31)
; 31)  ; 32)
; 32) 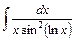 ;
; ; 34)
; 34)  ; 35)
; 35)  ; 36)
; 36) 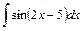 ;
;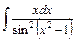 ; 38)
; 38)  ; 39)
; 39)  ; 40)
; 40) 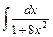 ;
; ; 42)
; 42)  ; 43)
; 43)  ; 44)
; 44)  ;
; ; 46)
; 46)  ; 47)
; 47) 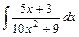 ; 48)
; 48)  ;
; ; 50)
; 50)  ; 51)
; 51)  ; 52)
; 52)  .
. ; 2)
; 2)  ;
; ; 4)
; 4)  ;
; ; 6)
; 6)  ;
;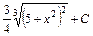 ; 8)
; 8)  ;
;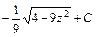 ; 10)
; 10) 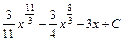 ;
;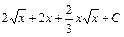 ; 12)
; 12)  ;
; ; 14)
; 14)  ;
; ; 16)
; 16)  ;
; ; 18)
; 18)  ;
; ; 20)
; 20)  ;
; ; 22)
; 22)  ;
;