 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Алгоритм обчислення похідної
Похідна функції
Приклад 1 За означенням похідної знайти похідні функцій: 1) 4) Розв’язання 1) Користуємось алгоритмом обчислення похідної.
Тоді
Аналітично можна дістати
2)
Тоді
3)
Тоді
4)
Можна довести, ми це зробимо пізніше, що для степеневої функції
5)
Тут використали еквівалентні нескінченно малі (8.10):
Тоді
6)
Тоді
Диференційованість функції Функція
де Теорема 1. Для того, щоб функція Зауваження. Із цієї теореми слідує, що поняття диференційованості функції в точці Теорема 2. Якщо функція Обернене твердження невірне! Існують неперервні функції, але не диференційовні в деяких точках неперервності. Наприклад, функція Дійсно
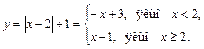
Розглянемо похідну зліва
(16*)
Функція буде диференційованою в точці
Правила диференціювання 1. Якщо
Наслідок. Похідна від суми будь-якого скінченного числа диференційованих функцій дорівнює сумі похідних цих функцій
2. Добуток двох диференційованих функцій
Наслідок. а) Похідна добутку
б) Якщо
3. Якщо
Ці твердження легко доводяться за означенням похідної (10.3). Скористаємось алгоритмом обчислення похідної. 1. Доведемо (17). Нехай
2. Доведемо (19),
тому що 3. Доведемо (21),
Приклад 2 Знайти похідні наступних функцій: 1) 3) 5) 7) 9) 11) Розв’язання 1)
тому що 2)
3)
4)
5)
6)
7)
8)
9)
10)
11)
12)
5. Похідна від оберненої функції Теорема. Якщо функція
Це тому, що
Приклад 3 Обчислити похідні функцій: 1) Розв’язання 1) Оберненою функцією до заданої є функція
2) Оберненою функцією до заданої є
3) Оберненою функцією до цієї є
4) Обернена функція до заданої
Поиск по сайту: |
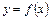 може бути знайдена за таким алгоритмом:
може бути знайдена за таким алгоритмом: . Надамо аргументу
. Надамо аргументу  приріст
приріст 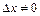 і знайдемо нарощене значення функції
і знайдемо нарощене значення функції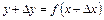 .
. . Знаходимо приріст функції
. Знаходимо приріст функції .
.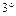 . Складаємо відношення
. Складаємо відношення  .
.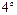 . Знаходимо границю цього відношення, якщо
. Знаходимо границю цього відношення, якщо 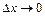 , тобто
, тобто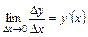 .
.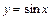 ; 2)
; 2) 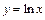 ; 3)
; 3) 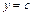 ,
, 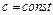 ;
;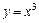 ; 5)
; 5)  .
.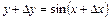 ;
;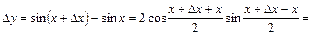
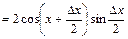 ;
;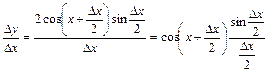 ;
;
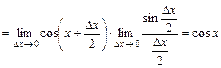 .
.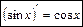 . (9)
. (9) . (10)
. (10)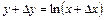 ;
; ;
;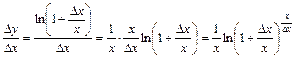 ;
;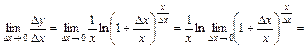
 .
.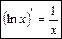 . (11)
. (11) ;
;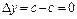 ;
; ;
; .
.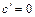 ,
, 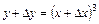 ;
;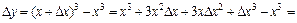
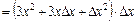 ;
; ;
; , тобто
, тобто 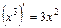 .
.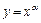 ,
,  похідна обчислюється за формулою
похідна обчислюється за формулою . (13)
. (13) ;
;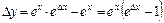 ;
; ;
;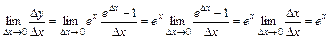 .
.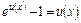 , якщо
, якщо  .
. (14)
(14)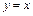
 ;
; ;
;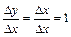 ;
;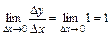 .
.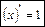 . (15)
. (15)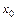 , якщо її приріст в цій точці можна подати у вигляді
, якщо її приріст в цій точці можна подати у вигляді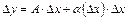 , (16)
, (16)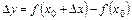 ,
, 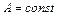 ,
,  – нескінченно мала функція при
– нескінченно мала функція при 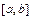 , позначають через
, позначають через 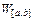 .
. (рис. 10.3). Вона неперервна на всій дійсній прямій, але не диференційовна в т.
(рис. 10.3). Вона неперервна на всій дійсній прямій, але не диференційовна в т. 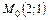 , похідна цієї функції в точці
, похідна цієї функції в точці 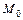 не існує.
не існує.
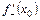 та справа
та справа 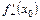 в точці
в точці 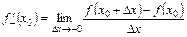 ;
;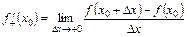 .
. означає, що графік функції в точці
означає, що графік функції в точці 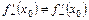 , то в точці
, то в точці 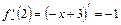 ;
; 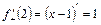 ,
, і тому функція
і тому функція 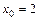 , хоча ця точка є точкою неперервності.
, хоча ця точка є точкою неперервності. та
та  – диференційовані функції від
– диференційовані функції від 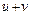 також є диференційованою функцією і
також є диференційованою функцією і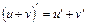 (17)
(17)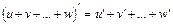 . (18)
. (18)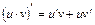 (19)
(19)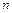 диференційованих функцій
диференційованих функцій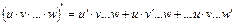 . (20)
. (20)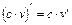 , (21)
, (21) , то відношення
, то відношення 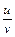 двох диференційованих функцій є функція диференційована і
двох диференційованих функцій є функція диференційована і . (22)
. (22) і
і 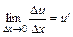 ,
,  .
.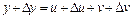 ;
;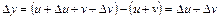 ;
;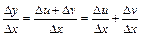 ;
;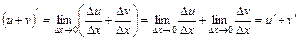 .
. .
. ;
;
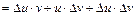 ;
; ;
;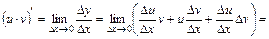
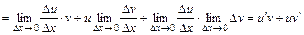 ,
,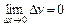 .
. .
.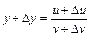 ;
;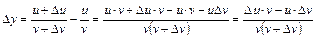 ;
;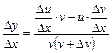 ;
;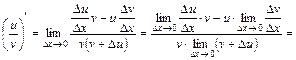
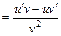 , тому що
, тому що 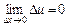 .
.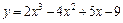 ; 2)
; 2) 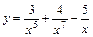 ;
;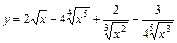 ; 4)
; 4) 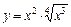 ;
; ; 6)
; 6)  ;
;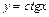 ; 8)
; 8)  ;
; ; 10)
; 10) 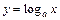 ;
; ; 12)
; 12) 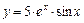 .
.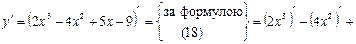

 ,
,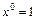 ;
;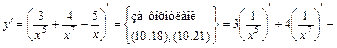
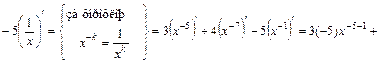
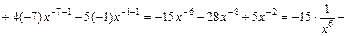
 ;
;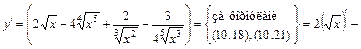
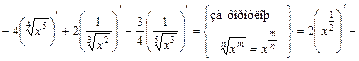

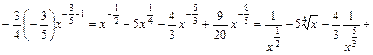
 ;
;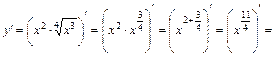
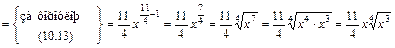 ;
;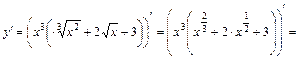
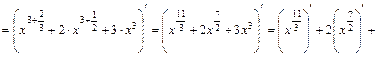
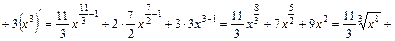
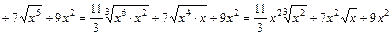 ;
;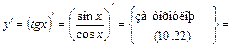
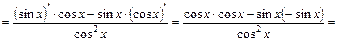
 ;
; (23)
(23)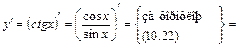
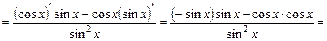
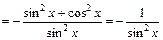 ;
;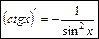 (24)
(24)
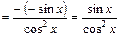 ;
;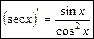 (25)
(25)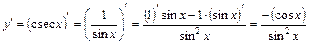 ;
;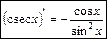 (26)
(26)
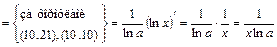 ;
; (27)
(27)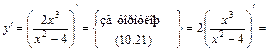

 ;
;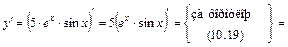
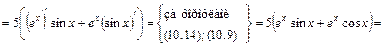
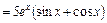 .
.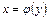 і її похідна обчислюється за формулою
і її похідна обчислюється за формулою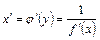 . (28)
. (28)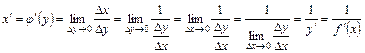 .
.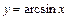 ; 2)
; 2) 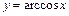 ; 3)
; 3) 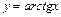 ; 4)
; 4) 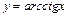 .
. ,
, 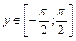 .
.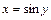 . За теоремою про похідну від оберненої функції маємо
. За теоремою про похідну від оберненої функції маємо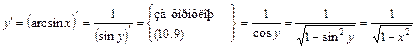 ;
; ; (29)
; (29) .
. . За теоремою про похідну від оберненої функції
. За теоремою про похідну від оберненої функції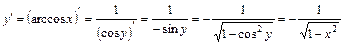 ;
; ; (30)
; (30) ,
,  .
.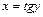 . Аналогічно прикладам 1) і 2) маємо
. Аналогічно прикладам 1) і 2) маємо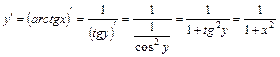 ;
;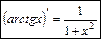 ; (31)
; (31)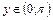 .
.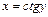 . Тоді
. Тоді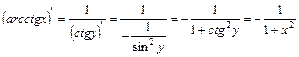 ;
; . (32)
. (32)