 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
В работе измеряется коэффициент вязкости масла ⇐ ПредыдущаяСтр 3 из 3
В трубке с маслом падают капли воды, коэффициент вязкости определяется по формуле:
где v- скорость падения капли воды, r- радиус капель,
g- ускорение свободного падения.
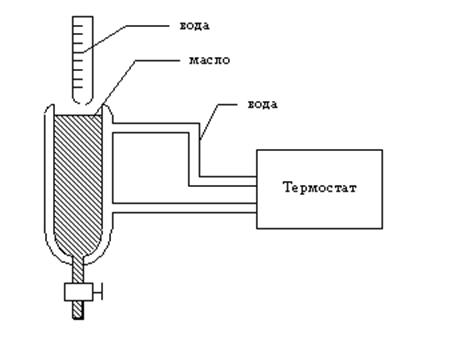
Задание и отчетность Прибор, с помощью которого производится экспериментальное определение h, изображен на рис.1.
Рис. 1.Экспериментальная установка для определения коэффициента вязкости.
1. Из пипетки капнуть одну каплю на чашечку торсионных весов, определить массу капли и рассчитать ее радиус. 2. Повторить п.1 3-5 раз и найти средний радиус. 3. При комнатной температуре капнуть каплю из вертикально расположенной пипетки в устье установки. Определить время прохождения капли между двумя фиксированными положениями (выбрать расстояние 15-20 см). 4. Повторить п.3 2 раза. Найти среднюю скорость падения. 5. Рассчитать значения вязкости для температур 30 0С, 40 0С, …95 0С.
Контрольные вопросы 1. Что такое вязкость? 2. В каких единицах измеряется коэффициент вязкости? 3. Какие силы действуют на шарик, падающий в жидкости? 4. Почему, начиная с некоторого времени, шарик движется равномерно? 5. Как подсчитать выталкивающую силу?
Литература 1. Кикоин В. Н. Кикоин А. П. Молекулярная физика.- М.: Наука., 1976. 2. Сивухин Л. В. Общий курс физики.- М.: Наука., 1975.
Р А Б О Т А № 6
Определение скорости испарения жидкости и изменение еЁ энтропии при испарении
Принадлежности: торсионные весы, секундомер, штангенциркуль, термометр, цилиндрический стаканчик, этиловый спирт.
Теория Процесс испарения – переход из жидкой среды в газообразную, является фазовым переходом первого рода, так как при этом поглощается тепло и изменяется плотность. Характеристикой испарения может служить его скорость. Скорость испарения численно равна массе жидкости, испаряющейся за одну секунду с 1 м2
Скорость испарения сильно зависит от температуры и химической природы вещества. Скорость испарения этилового спирта, бензина, эфира и некоторых других жидкостей настолько значительна, что с помощью аналитических весов можно следить за уменьшением массы жидкости, перешедшей в газовую среду, что и осуществляется в данной работе. Число микросостояний, которыми осуществляется данное макросостояние, называется термодинамической вероятностью этого макросостояния W. Оно служит количественной характеристикой теплового состояния тела, описывающей его стремление переходить в другие состояния. Тело, предоставленное самому себе, стремится перейти в состояние с большей вероятностью. Однако вычисление термодинамической вероятности является сложной задачей, так как: 1. практически чрезвычайно трудно подсчитать число различных комбинаций молекул, соответствующих тому или иному состоянию системы; 2. термодинамическая вероятность сложной системы равна произведению термодинамической вероятности ее частей. Поэтому для характеристики направленности процесса вводится другая, пропорциональная W, величина, называемая энтропией S. Больцман установил зависимость S=k lnW, где k - постоянная Больцмана. Энтропия тепловых процессов, происходящих в замкнутой системе, возрастает, и система стремится перейти из менее в более вероятное состояние. Таким образом, энтропия служит мерой неупорядоченности хаотического движения молекул. Обычно нас интересует изменение энтропии (
Изменение энтропии при любом конечном процессе (1®2)
Изменение энтропии жидкости, перешедшей в пар, если считать температуру перехода постоянной, определяется по формуле:
где r- удельная теплота испарения.
Задание и отчетность 1. Плавно отключить арретирующее устройство и вращая левый барабан добиться, чтобы правый указатель весов установился на красной линии. Вращением правого барабана установить начальный вес пустой чашки. 2. Закапать пипеткой в чашку весов исследуемую жидкость (2-3 капли) таким образом, чтобы масса жидкости и стаканчика не превышала верхний предел измерения весов (100 мг). 3. Вращением левого барабана торсионных весов удерживать положение стрелки на красной линии. 4. Через каждые 2 мин (для спирта) или 1 мин (для ацетона) записывать значения массы. 5. П.п. 3-4 повторять в течении 20 мин. 6. Рассчитать среднее изменение массы стаканчика за 2 мин (1мин). 7. Найти изменение массы жидкости в секунду с единичной поверхности. 8. Рассчитать изменение энтропии жидкости по формуле (4), определив температуру опыта по комнатному термометру. 9. Оценить погрешности измерений
ацетон C3H6O r =501,6 кДж/кг этанол (этиловый спирт) С2H5OH r =842,2 кДж/кг
Таблица 1
Контрольные вопросы 1. Что называется скоростью испарения? 2. Энтропия, ее свойства и термодинамический смысл. 3. Можно ли считать процесс испарения изотермическим?
Литература 1. Кикоин В. Н. Кикоин А. П. Молекулярная физика.- М.: Наука., 1976. 2. Сивухин Л. В. Общий курс физики.- М.: Наука., 1975.
Р А Б О Т А № 7 ОПРЕДЕЛЕНИЕ ОТНОШЕНИЯ CP/CV ПО СКОРОСТИ ЗВУКА В ГАЗЕ И ЕЁ ЗАВИСИМОСТИ ОТ ТЕМПЕРАТУРЫ
Принадлежности:звуковой генератор, электронный осциллограф, микрофон, телефон, стеклянная трубка, лабораторный трансформатор, датчик температуры.
Теория Отношение теплоемкостей газов g =Ср/Сv играет важную роль в теории идеальных газов, т.к. через него определяется число степеней свободы молекул Существует несколько способов измерений Ср/Сv. Наиболее удобным и точным из них следует считать метод, основанный на измерении скорости звука. В механике скорость распространения звука определяется формулой:
где r –плотность газа, P–давление газа. Качественно распространение звука в идеальном газе с молекулярной точки зрения можно описать так. Колеблющееся тело (мембрана) подвергает газ периодическому сжатию и разрежению. При сжатии кинетическая энергия молекул возрастает, а сжатый слой газа нагревается. При разряжении же кинетическая энергия молекул уменьшается, а слой расширившегося газа охлаждается. Колебания плотности и связанные с ними колебания температуры в звуковой волне происходят настолько быстро, а теплопроводность газа настолько мала, что для таких процессов теплообмен не играет никакой роли. Разности температур между сгущениями и разрежениями воздуха в звуковой волне не успевают выравниваться, благодаря чему процесс распространения звука в газе надо рассматривать как адиабатический. Полагая, что для адиабатического процесса (процесса, происходящего без подвода и отвода тепла) dQ=0, dU=CvdT, dA=PdV, получим из первого начала термодинамики CvdT+PdV=0 . (2) Из уравнения Клайперона–Менделеева
исключая dT, получим CpPdV+CvVdP=0. (4) Введем обозначение g=Cp/Cv , (5) тогда gPdV+VdP=0 . (6) Если в уравнение (6) вместо объема ввести плотность r=m/V, то получим gPdr – rdP=0 , (7) отсюда
Подставляя (8) в (1), получим скорость распространения звука в газе
где R–газовая постоянная, T–температура, m-молярная масса. Преобразуя эту формулу, найдем:
Таким образом, для определения показателя адиабаты достаточно измерить температуру газа и скорость распространения звука в газе (молярный вес газа предполагается известным). В данной работе скорость распространения звука определяется в воздухе в диапазоне температур от комнатной до 95-970С. Установка для измерения скорости звука изображена на рис.1.
Рис. 1.Установка для измерения скорости звука.
Звуковые колебания в трубе возбуждаются телефоном (электродинамиком). Колебания улавливаются микрофоном. Мембрана телефона приводится в движение переменным током звуковой частоты от звукового генератора ЗГ–10. Возникающий в микрофоне сигнал наблюдается на осциллографе СИ–1. Звуковая волна, распространяющаяся вдоль трубки, испытывает многократное отражение от торцов трубки. Звуковые колебания в трубе являются наложением падающих и отраженных волн, и вообще говоря, очень сложны. Картина резко упрощается, если длина трубы равна целому числу полуволн, т. е.
где l– длина волны звука в трубе, n– любое целое число, L-длина трубы. Если условие (11) выполнимо, то волна, отраженная от заднего торца трубы, вернувшаяся к ее началу и вновь отраженная, совпадает по фазе с падающей. Аналогичным образом совпадают по фазе волны, движущиеся от заднего торца к переднему, после второго отражения и после всех последующих отражений. Совпадающие по фазе волны усиливают друг друга. Амплитуда звуковых колебаний резко возрастает – наступает резонанс. Скорость звука v связана с его частотой f и с длиной волны l соотношением v=lf . (12) Если плавно изменять частоту звукового генератора, а следовательно длину звуковой волны, то возникновение резонанса можно наблюдать на осциллографе по резкому увеличению амплитуды колебаний. Для последовательных резонансов имеем: ln=2L/n , ln+1=2L/(n+1) , v=2L(fn+1 -fn)=2L(fn+2 - fn)/2 . (13) ln+k =2L/(n+k) , v=2L(fn+k-fn)/ k . (14) L=0,8 м.
Задание и отчетность 1. Включите электронный осциллограф и звуковой генератор и дайте нагреться 5–7 мин. После этого включите тумблер “ЛУЧ” и поверните ручку “ЯРКОСТЬ”. При этом должна быть видна на экране линия. 2. Подберите напряжение на выходе генератора так, чтобы на осциллографе наблюдались колебания достаточной амплитуды. Убедитесь в том, что колебания имеют неискаженную синусоидальную форму. Если форма колебаний искажена, уменьшайте амплитуду сигнала, поступающего с генератора, пока искажения не прекратятся. 3. Измерения при комнатной температуре: а). Плавно увеличивая частоту генератора, запишите ряд последовательных резонансных значений частоты, отмечая момент резонанса по увеличению амплитуды колебаний на экране осциллографа. Убедитесь в повторяемости результатов, производя измерения в обратном порядке. б). Полученные результаты запишите в таблицу 1 и изобразите на графике, откладывая по оси абсцисс номер резонанса, а по оси ординат – резонансную частоту. Необходимо получить не менее 20 последовательных резонансов. Через полученные точки проведите наилучшую прямую. Тангенс угла наклона определяет величину v (формула 14). в). Вычислите значение g =Cp/Cv по формуле (10). Оцените ошибку полученного результата. 4. Измените при помощи ЛАТРа температуру газа внутри трубки на 100 С. Определите fn и fn+k при фиксированном числе k . По формуле (14) определите скорость звука при этой температуре и g по формуле (10). 5. Повторите п.4 до достижения t=95-970С. Полученные значения v и g занесите в таблицу 2. Постройте графики зависимости v(T) и g (T).
Таблица 1.
Таблица 2.
Контрольные вопросы 1. Что называется адиабатическим процессом? 2. Как вывести уравнение адиабатического процесса для идеального газа из I закона термодинамики? 3. Почему скорость распространения звука считают адиабатическим процессом? 4. Приведите примеры естественных и технических адиабатических процессов. 5. Чему равна величина отношения Cp/Cv для двух атомных газов согласно молекулярно–кинетической теории идеальных газов? 6. Какова роль g =Cp/Cv в теории и практике? 7. Каковы основные трудности классической теории теплоемкости идеальных газов? 8. При каких частотах наблюдается дисперсия распространения звука в газах? Почему? 9. Чем объясняется зависимость v(T) и g (T).
Литература 1. Р. В. Телеснин. Молекулярная физика.- Высшая школа.- гл.3., §37, 38, 42. 2. Л. Д. Ландау, А. И. Ахнезер, Е. М. Лившиц. Курс общей физики.- Наука., 1965. 3. С. Э. Хайкин Физические основы механики.- Наука., 1971.- гл. 19., §154. 4. С. Э. Фриш, А. В. Тиморева. Курс общей физики.- Физматгиз., 1962.- т.1., §115. 5. И. В. Радченко. Молекулярная физика.- Наука., 1965.- гл.5., §58, 59. 6. Д. В. Сивухин. Общий курс физики.- Наука., 1975.- т.2 гл.2., §15,18, 19, 21, 23, 24. 7. И. К. Кикоин, А. К. Кикоин. Молекулярная физика.- Физматгиз., 1963.- гл.2., §7, 8.
Поиск по сайту: |
 (8)
(8) ,
, 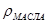 -плотности жидкостей,
-плотности жидкостей,


 свободной поверхности. Если масса испаряющейся жидкости
свободной поверхности. Если масса испаряющейся жидкости  , площадь свободной поверхности жидкости в случае цилиндрического сосуда
, площадь свободной поверхности жидкости в случае цилиндрического сосуда  , где d - диаметр сосуда и время испарения
, где d - диаметр сосуда и время испарения  , то скорость испарения равна
, то скорость испарения равна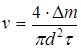 . (1)
. (1) ) какого-либо процесса. Из формулы Клаузиуса при изотермическом процессе
) какого-либо процесса. Из формулы Клаузиуса при изотермическом процессе . (2)
. (2) . (3)
. (3) , (4)
, (4) и
и  . Результаты измерений и расчетов занесите в таблицу 1.
. Результаты измерений и расчетов занесите в таблицу 1.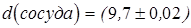 мм
мм


 . Кроме того, эта величина входит в уравнение адиабаты. Роль этой величины заключается еще в том, что, зная ее, можно не прибегать к измерениям Сv, которые всегда трудны. Значение Сv можно получить из измеренных значений Ср и g.
. Кроме того, эта величина входит в уравнение адиабаты. Роль этой величины заключается еще в том, что, зная ее, можно не прибегать к измерениям Сv, которые всегда трудны. Значение Сv можно получить из измеренных значений Ср и g. (1)
(1)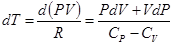 ; (3)
; (3) . (8)
. (8) , (9)
, (9) . (10)
. (10)
 (11)
(11)