 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Описание лабораторной установки. Хаотичность теплового движения молекул газа и непрерывные соударения приводят кСтр 1 из 3Следующая ⇒
Теория Хаотичность теплового движения молекул газа и непрерывные соударения приводят к постоянному перемещению частиц, изменению их скорости и энергии. Если в газе существует пространственная неоднородность плотности, температуры или скорости упорядоченного движения, то движение молекул выравнивает эти неоднородности. При этом в газе протекают явления переноса. К ним относятся диффузия (направленный перенос массы), теплопроводность (направленный перенос энергии), внутреннее трение или вязкость (направленный перенос количества движения). Рассмотрим явление внутреннего трения в газах. Если скорость в потоке газа меняется от слоя к слою, то на границе смежных слоев действует сила внутреннего трения, величина которой определяется эмпирической формулой:
где
S – величина поверхности, на которую действует сила. Рассмотрим это явление с позиции молекулярно–кинетической теории газов. Выделим два соприкасающихся слоя газа (рис.1).
где n0 – число молекул в единице объема. Вследствие неодинаковости скоростей упорядоченного движения U1 >U2 молекулы в различных слоях обладают в среднем различным количеством движения. Попав в другой слой, молекула сталкивается с его молекулами. В результате чего она либо отдает избыток своего количества движения (при переходе из слоя 1 в слой 2), либо увеличивает свое количество движения ( при переходе из слоя 2 в слой 1). Из первого слоя за время
где m – масса молекулы. За это время из слоя 2 в слой 1 молекулы перенесут количество движения:
Изменение количества движения второго слоя будет равно:
Согласно основному закону динамики, изменение количества движения равно импульсу действующей силы:
Сила F – есть сила внутреннего трения, равная:
С учетом выражения (2) выражение (4) приобретает вид:
Разность скоростей (U1 –U2 ) можно выразить через градиент скорости Тогда можно записать:
Откуда разность скоростей равна:
С учетом последнего соотношения выражение (5) приобретает вид:
Произведение концентрации молекул на массу молекул есть плотность газа:
Окончательно получаем:
Сравнивая полученное выражение с эмпирической зависимостью (1) видим, что молекулярно–кинетическая теория газов позволяет связать величину коэффициента вязкости с параметрами, характеризующими движение молекул:
Соотношение (7) позволяет получить по экспериментально определенной величине важную характеристику движения молекул – среднюю длину свободного пробега l:
Средняя скорость движения молекул зависит от температуры Т и определяется выражением:
где R – газовая постоянная, m – молярный вес. Плотность газа является функцией давления Р и температуры Т:
С учетом соотношений (9) и (10) формула для нахождения средней длины свободного пробега принимает вид:
Из формулы (11) видно, что для нахождения средней длины свободного пробега молекул газа необходимо знать величину давления Р и температуры Т. Если известна средняя длина свободного пробега молекул, то можно оценить значение эффективного диаметра молекул s. Как следует из молекулярно–кинетической теории газов, величина l связана с эффективным диаметром следующим соотношением:
где k– постоянная Больцмана; откуда:
Значение эффективного диаметра молекул имеет большое значение при анализе различных физических явлений, таких как упругое и неупругое рассеяние частиц (фотонов, нейтронов и др.) Существуют различные способы определения коэффициента вязкости газов. В настоящей работе применяется метод капилляра. Рассмотрим движение воздуха в трубке круглого сечения. При малых скоростях потока движение оказывается ламинарным (слоистым). При увеличении скорости потока движение становится турбулентным и слои перемешиваются. При турбулентном движении скорость в каждой точке быстро меняет величину и направление, сохраняется только средняя величина скорости. Характер движения газа в трубке определяется безразмерным числом Рейнольдса:
где v – скорость потока, r– радиус трубки, r- плотность движущейся среды, h – ее коэффициент вязкости. В гладких трубках круглого сечения переход от ламинарного движения к турбулентному происходит при R =1000. При ламинарном течении объем V газа, протекающий за время t по трубе длины l, определяется формулой Пуазейля:
В этой формуле( Р1 – P2) - разность давлений в двух выбранных сечениях 1 и 2, расстояние между которыми равно
Выясним условия, при которых справедлива формула (15). Как уже было сказано выше, для этого прежде всего необходимо, чтобы с достаточным запасом выполнялось неравенство R<1000. Необходимо также, чтобы при течении сквозь трубку не происходило существенного изменения удельного объема воздуха (при выводе формулы удельный объем жидкости считается постоянным). Для газа это предположение не выполняется лишь в тех случаях, когда перепад давления вдоль трубки мал по сравнению с самим давлением. В нашем случае давление газа равно атмосферному (10 см водяного столба), а перепад давлений составляет не более 5 см водяного столба, т. е. 0,5% от атмосферного.
Описание лабораторной установки Прибор, с помощью которого производится экспериментальное определение h, изображен на рис.2.
Задание и отчетность 1. Откройте кран 5, отрегулируйте скорость вытекания жидкости из газометра так, чтобы разность уровней спирта в коленах манометра h не превышала 2–2,5 см. 2. Измерьте объем газа прошедшего через капилляр за время t по количеству воды, выливающейся из газометра (V) при установившемся режиме течения воздуха через капилляр. Проделайте измерения при трех различных значениях разности давления 3. Измерьте атмосферное давление и температуру воздуха в комнате, сравните ее с температурой жидкости в стакане. Рассчитайте плотность воздуха. По формуле (16) подсчитайте коэффициент внутреннего трения воздуха. 4. Убедитесь в том, что течение воздуха в капилляре ламинарное, для этого вычислите число Рейнольдса:
где скорость Полученные результаты занесите в таблицу 1. Таблица 1
5. Включите нагреватель 8 в сеть, увеличьте температуру жидкости на 100-120. После выключения нагревателя повторите п.п. 2-4. Полученные результаты занесите в таблицу 1. 6. Повторите п.5 до тех пор, пока температура жидкости в стакане не достигнет 95-97 0С. 7. Определите среднее значение, <h> отклонения результатов от среднего значения 8. Вычислите среднюю квадратичную ошибку отдельного измерения:
и среднюю кадратичную ошибку результатов измерений. 9. По формулам (8), (9) и (13) используя полученное значение коэффициента вязкости, найдите l и s для каждой температуры. Результаты измерений и расчетов занесите в таблицу 2. Таблица 2
10. Постройте графики зависимости h=h(T), s=s(T), l=l(T).
Контрольные вопросы 1. Пользуясь молекулярно–кинетической теорией, покажите, от каких величин зависит коэффициент внутреннего трения в газах? 2. Какова связь коэффициента внутреннего трения с коэффициентами, характеризующими другие явления? 3. Молекулярно–кинетический смысл числа Рейнольдса. 4. Если течение газа в трубке является ламинарным, по какому закону меняются скорости течения отдельных слоев газа от стенок к оси трубки? 5. Зависит ли коэффициент внутреннего трения, длина свободного пробега воздуха от температуры и давления? Если зависит, то почему? 6. Что такое эффективный диаметр молекулы? От чего он зависит? 7. Какой вид имеет уравнение переноса в феноменологической записи 8. Что такое средняя длина свободного пробега молекул в газе? Может ли она измеряться на опыте? 9. Как получается уравнение переноса в кинетической теории газов? Как раскрывается молекулярно–кинетическое выражение коэффициента переноса, введенного в феноменологическое уравнение? 10. Каковы границы применимости уравнений переноса? В чем трудность применения этих уравнений к разреженному газу?
Литература 1. Кикоин В. Н. Кикоин А. П. Молекулярная физика.- М.: Наука., 1976. 2. Телеснин Р. Е. Молекулярная физика.- М.: Высшая школа., 1973. - гл.7. 3. Ландау П. Д. Акнезер А. Лифшиц. Курс общей физики- Механика и молекулярная физика. - М.: Наука., 1969.- гл.15. 4. Сивухин Л. В. Общий курс физики. - М.: Наука., 1975. - т.2.
Р А Б О Т А № 4
Определение коэффициента теплопроводности металлов
Принадлежности: нагреватель, мост с термопарой, стержни из различных металлов (Al, Cu, Fe, латунь).
Теория Распределение температуры Т вдоль нагреваемого с одного конца стержня, ось которого совпадает с осью Х, дается решением дифференциального уравнения вида:
причем
Здесь Т0 – температура окружающего стержень пространства,
Р – периметр поперечного сечения стержня, S – площадь поперечного сечения стержня, l – искомый коэффициент теплопроводности. Это уравнение может быть выведено из следующих соображений. Рассмотрим отрезок стержня длиной dх. Количество тепла, проходящего через стержень сечением S (сечение соответствует точке х), будет:
Количество тепла, проходящего через сечение, соответствующее точке х+dх, равно:
Через боковую поверхность отрезка стержня теряется количество тепла:
При стационарном процессе
Разлагая это выражение в ряд и пренебрегая бесконечно малыми высших порядков, можем написать
откуда
обозначая
получим:
Решение уравнения имеет вид:
Полагая, что при х=0 температура Т=Т0 , а сам стержень бесконечно длинный, т.е. при х®¥, Т=Т0 , получим:
откуда
Количество теплоты, теряемое стержнем через боковую поверхность
что может быть записано в виде:
Интегрируя это выражение в пределах от 0 до ¥, получим:
Используя уравнение (1 ), находим, что
Подставляя величину a из уравнения (2), получаем окончательно:
Для определения теплопроводности, согласно этой формуле, необходимо знать количество тепла q, отдаваемое стержнем через поверхность при стационарном режиме, температуру нагреваемого конца стержня Т1, температуру Т в какой–либо точке стержня нa расстоянии х от нагреваемого конца, площадь поперечного сечения стержня S и температуру окружающей среды Т0. Практически, конечно, невозможно иметь бесконечно длинный стержень, однако, чем он длиннее, тем точнее может быть измерена величина коэффициента теплопроводности. Найдем величину ошибки, полагая, что стержень имеет длину l. Из уравнения (3), интегрируя его от х = l до х = ¥ , получим:
Разделив это соотношение на выражение (4), полученное путем интегрирования того же выражения (3) в пределах от х = 0 до х = ¥, получим:
Это выражение и даст величину ошибки, допускаемой при определении теплоты q, когда принимают стержень длины l за бесконечно длинный.
Поиск по сайту: |
 , (1)
, (1)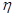 – коэффициент внутреннего трения (коэффициент вязкости);
– коэффициент внутреннего трения (коэффициент вязкости); – градиент скорости, характеризующий быстроту изменения скорости от слоя к слою;
– градиент скорости, характеризующий быстроту изменения скорости от слоя к слою; Пусть слои движутся со скоростями U 1 и U2 , U1 >U2. Каждая молекула газа участвует в двух движениях: упорядоченном со скоростью U и хаотическом тепловом, средняя скорость которого <v> >> U.
Пусть слои движутся со скоростями U 1 и U2 , U1 >U2. Каждая молекула газа участвует в двух движениях: упорядоченном со скоростью U и хаотическом тепловом, средняя скорость которого <v> >> U. Вследствие хаотического движения происходит непрерывный переход молекул из одного слоя в другой. За время
Вследствие хаотического движения происходит непрерывный переход молекул из одного слоя в другой. За время 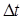 через поверхность S переходит из слоя в слой : из первого во второй и из второго в первый одинаковое число молекул.
через поверхность S переходит из слоя в слой : из первого во второй и из второго в первый одинаковое число молекул. , (2)
, (2)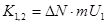 ,
,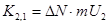 .
.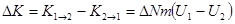 . (3)
. (3) .
. . (4)
. (4) . (5)
. (5)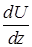 . Обозначим скорость в месте раздела слоев через U. Далее учтем, что перенос количества движения осуществляется только теми молекулами, которые находятся от границы раздела слоев на величину средней длины свободного пробега.
. Обозначим скорость в месте раздела слоев через U. Далее учтем, что перенос количества движения осуществляется только теми молекулами, которые находятся от границы раздела слоев на величину средней длины свободного пробега.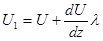 ;
;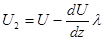 .
. .
.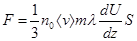 .
. .
. (6)
(6)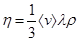 . (7)
. (7)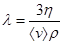 . (8)
. (8)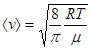 , (9)
, (9)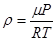 . (10)
. (10) . (11)
. (11)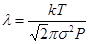 , (12)
, (12)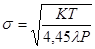 . (13)
. (13) , (14)
, (14)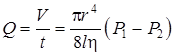 . (15)
. (15)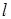 . Величину Q обычно называют расходом. Формула (15) позволяет определить вязкость газа по его расходу, т.е. :
. Величину Q обычно называют расходом. Формула (15) позволяет определить вязкость газа по его расходу, т.е. : . (16)
. (16)

 , измеряемая спиртовым манометром 3. Чтобы через капилляр проходил воздух с различной температурой, перед капилляром помещают сосуд 4 с подогреваемой жидкостью, температура которой фиксируется с помощью термометра 7. Для определения расхода воздуха служит мерный стакан 6. Время наполнения стакана определяется секундомером.
, измеряемая спиртовым манометром 3. Чтобы через капилляр проходил воздух с различной температурой, перед капилляром помещают сосуд 4 с подогреваемой жидкостью, температура которой фиксируется с помощью термометра 7. Для определения расхода воздуха служит мерный стакан 6. Время наполнения стакана определяется секундомером. ,
,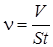 , S – сечение капилляра (S=pr2 , r=0,52 мм).
, S – сечение капилляра (S=pr2 , r=0,52 мм).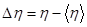 ,
, 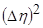 для каждой температуры.
для каждой температуры.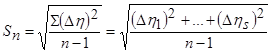 ,
, 

 , (1)
, (1) . (2)
. (2) – коэффициент теплоотдачи,
– коэффициент теплоотдачи,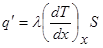 .
. .
.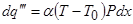 .
.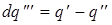 , т. е.
, т. е.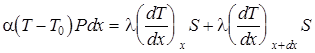 .
. ,
,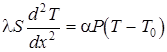 ;
;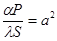 ,
, .
.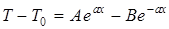 .
. ,
,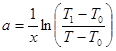 . (2)
. (2)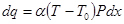 ,
,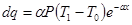 . (3)
. (3) . (4)
. (4) . (5)
. (5)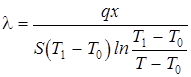 . (6)
. (6)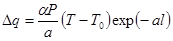 .
.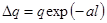 . (7)
. (7)