 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Описание лабораторной установки. В задаче определяется теплопроводность латунного стержня
В задаче определяется теплопроводность латунного стержня, конец которого нагревается в электропечи (рис. 1).
Рис. 1.Установка для определения коэффициента теплопроводности металлов (электропечь).
Количество тепла, отдаваемого печью в единицу времени, определяется конструкцией установки в нашей работе: q=0,24I0 U0 =12,9 Вт, где I0 и U0 – определяемые приборами напряжение на концах обмотки печи и сила тока в цепи обмотки. Температура печи (конца стержня) Т1 определяется термопарой. Теплота Q частично идет на создание теплового потока q, обусловленного теплопроводностью стержня, частично в окружающее печь пространство q1, так что Q=q1 +q. Для уменьшения ошибки в определении q необходимо, чтобы величина q1 была мала по сравнению с величиной q, для этого печь помещена в специальное устройство. Температура стержня Т измеряется в пяти точках, при этом температура в точке, ближайшей к нагревателю, является температурой печи.
Задание и отчетность 1. В начале определяют площадь поперечного сечения S исследуемого стержня, для этого измеряют его диаметр, затем масштабной линейкой измеряют длину стержня l и расстояние хi от нагреваемого конца стержня до каждой из четырех точек, высверленных в стержне, принимая за нагреваемый конец ближайшее к печи отверстие. 2. Вставить датчик термопары в первое отверстие стержня, закрепленного длинным концом в нагревателе. 3. Включить измерительный мост УИП-60М тумблером Т. 4. Включить печь в сеть и прогреть ее 20¸25 мин. 5. Вращая ручку потенциометра П добиться, чтобы стрелка гальвонометра G установилась на нуле. Показания термоЭДС снять со шкалы, связанной с потенциометром. Провести измерения ЭДС во всех точках стержня. Результат занести в таблицу, найти среднее значение для каждой точки. Перевести среднее значение ЭДС e в соответствующую ей температуру по следующей формуле
где t0 - измеряемая температура,
6. Сменить стержень на другой из другого металла. ( Осторожно, возможен ожог! ) 7. Повторить п.п. 2-5 8. Тумблером Т отключить питание измерительного моста. 9. Построить графики зависимости Т (х). 10. С учетом формул (6) и (8) рассчитать для всех контрольных точек и различных материалов величину коэффициента теплопроводности по формуле
где индекс i соответствует номеру контрольной точки. 11. Для данного материала рассчитать среднее значение коэффицента теплопроводности, абсолютную ошибку и окончательный результат записать в виде:
Контрольные вопросы 1. Объяснить полученные закономерности в значениях l для различных металлов. 2. Объяснить фононный и электронный механизмы переноса тепла в твердых телах. 3. Что такое коэффициент теплопроводности?
Литература 1. Кикоин В. Н. Кикоин А. П. Молекулярная физика.- М.: Наука., 1976. 2. Сивухин Л. В. Общий курс физики.- М.: Наука., 1975.
р а б о т а № 5
Исследование температурной зависимости коэффициента вязкости в жидкости
Принадлежности: термостат, трансформаторное масло, экспериментальная установка, весы торсионные.
Теория метода На капельку воды (или на твердый шарик), падающий в вязкой жидкости, действуют 3 силы: сила тяжести, подъемная сила (закон Архимеда) и сила сопротивления движению, обусловленная силами внутреннего трения жидкости. При движении шарика слой жидкости, граничащий с его поверхностью, прилипает к шарику и движется со скоростью шарика. Таким образом, при вычислении сопротивления среды следует учитывать трение отдельных слоев жидкости друг о друга, а не трения шарика о жидкость. Если шарик падает в жидкость, простирающейся безгранично по всем направлениям, не оставляя за собой никаких завихрений (малая скорость падения, маленький шарик), то, как показал Стокс, сила сопротивления равна:
где h -коэффициент внутреннего трения жидкости, v -скорость шарика, r -его радиус. Вывод этой формулы довольно сложен и поэтому не может быть приведен здесь, его можно найти в специальной литературе. Однако вид соотношения, определяющего силу f , можно с точностью до постоянного множителя установить исходя из соображений размерностей. Опыт показывает, сила сопротивления будет тем больше, чем больше коэффициент внутреннего трения h, радиус r и скорость v падающего шарика. Таким образом, можно записать
но
Сравнивая соотношения (2) и (3) нетрудно видеть, что rxvy должно иметь размерность
Следовательно Множитель этим методом не может быть определен, он получается равным 6p, если решить задачу гидродинамики вязкой жидкости. В случае падения шарика в жидкости уравнение движения имеет вид
Здесь r- плотность вещества шарика (капелька жидкости), r1- плотность жидкости (трансформаторного масла), g- ускорение силы тяжести. Все три силы, входящие в правую часть уравнения (4) будут направлены по вертикали: сила тяжести – вниз, подъемная сила и сила сопротивления – вверх. Сила сопротивления с увеличением скорости движения шарика возрастает, а ускорение уменьшается и, наконец, шарик достигает такой скорости, при которой ускорение становится равным нулю, тогда уравнение примет вид
В этом случае шарик движется с постоянной скоростью v0 . Такое движение шарика (капелька воды) называется установившимся. Решая уравнение (5) относительно коэффициента внутреннего трения, получаем
Зная величины, находящиеся в правой части равенства можно определить коэффициент внутреннего трения жидкости. Практически невозможно осуществить падение шарика в безграничной среде, так как всегда жидкость находится в каком-то сосуде, имеющем стенки. Если шарик падает вдоль оси цилиндрического сосуда радиуса R, то учет наличия стенок приводит к следующему выражению для коэффициента вязкости:
Поиск по сайту: |

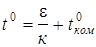 , (8)
, (8) - температура окружающей среды (0С),
- температура окружающей среды (0С), .
.

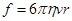 , (1)
, (1) , (2)
, (2)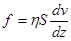 . (3)
. (3) , т.к.
, т.к. , а
, а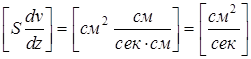 ;
; 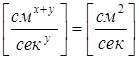 .
. ;
; 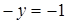 ; откуда
; откуда  ,
, 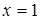 .
. .
. . (4)
. (4)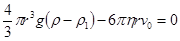 . (5)
. (5) . (6)
. (6) . (7)
. (7)