 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Оптимизация изменения плотности воздуха от высоты
Из курса общей физики мы знаем, что плотность воздуха определяется формулой:
где Но исследуя экспериментальные данные зависимости плотности воздуха от высоты, указанные в книге А.В. Солодова «Инженерный справочник по космической технике» (см. Приложение 1).
1 – по формуле 1.4.1 и 2 – экспериментально. Видно не точность формулы (1.4.1). Для решения этой проблемы будем применять численные методы для более точного результата. Используем метод, рассмотренный выше (метод линейной интерполяции пункт 1.4) в промежутке
Коэффициенты
Приравняем к нулю частные производные:
Выполнив преобразования, получим систему уравнений с тремя неизвестными (a0,a1,a2).
Введем обозначения:
Определим неизвестные коэффициенты a0,a1,a2
Необходимое условие: определитель системы
В результате мы можем с большей точности узнать плотность воздуха на любой высоте. Моделирование полета Для дальнейших расчетов возьмем межконтинентальную баллистическую ракету Р-9 / Р-9А (8К75)SS-8/(Sasin). Для которой в справочнике определены основные параметры: Начальная масса Диаметр ракеты Скорость отделяющихся частиц Доопределим параметры атмосферы: Плотность воздуха на поверхности Земли Высота над уровнем моря Радиус Земли Масса Земли Скорость вращения Земли на экваторе Постоянная тяготения Земли Используя начальные условия и систему уравнений можно определить траекторию движения МБР методом дифференцирования описанный в пункте 1.3. Так как мы дифференцируем уравнения дискретно с некоторым шагом, то это означает, что МБР прекратит дальнейшее движение только в случае, когда высота, на которой находится МБР, станет меньше нуля. Для устранения этого недочета будем использовать метод, описанный в пункте 1.4, но применим ее для нашего случая:
Будем искать коэффициенты a и b переменными
В нашем случае Определив угол отклонения, при котором высота МБР будет равна уровню Земли. Найдем дальность полета МБР: Время работы двигателя определяется формулой:
где
Теперь мы в состоянии определить траекторию движения МБР при данных начальных условиях.
Глава 2. Результаты
Поиск по сайту: |
 (1.4.1)
(1.4.1) – высота над уровнем моря (
– высота над уровнем моря (  ),
),  – высота МБР над уровнем Земли,
– высота МБР над уровнем Земли,  – плотность воздуха на уровне Земли
– плотность воздуха на уровне Земли  .
.
 , а в промежутке
, а в промежутке  используем метод параболической аппроксимации. Такая аппроксимация является не линейным, многочленом второй степени.
используем метод параболической аппроксимации. Такая аппроксимация является не линейным, многочленом второй степени.
 определяются по методу наименьших квадратов. Запишем квадратичное отклонение.
определяются по методу наименьших квадратов. Запишем квадратичное отклонение.
























 , где
, где 


 , в результате получаем
, в результате получаем 
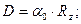

 – масса боеголовки. Для более реалистичного полета будем учитывать массу оболочки ступени, для этого добавим к этой формуле коэффициент
– масса боеголовки. Для более реалистичного полета будем учитывать массу оболочки ступени, для этого добавим к этой формуле коэффициент  , который показывает отношения массы ступени к массе топлива.
, который показывает отношения массы ступени к массе топлива.