|
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Определение аберраций объектива ⇐ ПредыдущаяСтр 5 из 5
На основании формул (9), (10) и (11), учитывая найденные аберрации окуляра и призмы, получим: Ds¢об= -(-0,31+0,097) =0,213 мм, Dy¢к,об = -0,02+0,03 = 0,01 мм, Ds¢l1,l2,об = -(-0,06+0,121) =-0,061 мм.
Мы должны рассчитать объектив со следующими характеристиками и аберрациями: фокусное расстояние f ¢об= 80 мм, относительное отверстие 1:4, угловое поле 2w=12°, сферическая аберрация Ds¢об=0,213 мм, меридиональная кома Dy¢к,об=0,01 мм хроматическая аберрация положения Ds¢l1,l2,об =-0,061 мм. Простейшим вариантом решения является двухлинзовый склеенный объектив. Расчет двухлинзового склеенного объектива может быть выполнен по одному из известных способов, изложенных в литературе [4, [5], [6], [7]]. Рассмотрим способ расчета двухлинзового склеенного объектива, разработанный проф. Г.Г. Слюсаревым [5]. Расчет по этой методике выполняется с помощью специальных таблиц [6, 7], позволяющих выбрать такую пару стекол, при которой можно исправить хроматизм положения, сферическую аберрацию и уменьшить меридиональную кому. Таблицы [6] содержат 11 марок флинтовых стекол и 17 марок кроновых стекол, объединенных в 142 комбинации, для которых рассчитаны значения P0, jk, Q0 для хроматического параметра C в диапазоне значений +0,0025…–0,005. За основную длину волны принято l0=589,3 нм (D), за дополнительные длины волн l1=486,13 нм (F) и l2=656,28 нм (C) Рассмотрим пример расчета объектива по методике профессора Г.Г. Слюсарева. а) Осуществляем переход от заданных аберраций объектива к основным аберрационным параметрам Р W и С объектива (при Sdоб=0). Воспользуемся формулами
где SII=spP/f ¢+ W. Формулы даны с учетом приведения величин Р, W и С к фокусному расстоянию объектива, равному единице. Из формулы (12) получим значение параметра W=-2f ¢ Dy¢к,III / 3m2tgw1=-2×80×0,01/[3×25×(-0,105)]=0,203, где для наклонного пучка, проходящего через входной зрачок объектива, с учетом виньетирования m=5 мм. Из формулы (14) получим параметр С=Ds¢l1,l2/f ¢ =-0,061/80=-0,000763. б) Вычисляем параметр Р0 по формуле Р0=Р-0,85(W-W0)2 где W0 принимаем равным 0,1 для комбинации стекол, когда кроновая линза находится впереди. При выборе относительного расположения флинтовой и кроновой линз следует руководствоваться правилом: если значение W<0,8, то предпочтительнее комбинация «крон впереди», поскольку она имеет меньшие значения сферической аберрации высшего порядка: Р0 =-0,341 -0,85×(0,203 –0,1)2 = -0,350. в) По таблице-номограмме [6, с. 40] для Р0=-0,350 и С=-0,000763 находим, что этим значениям соответствует 18-я клетка, для которой имеются следующие пары стекол БК8-ЛФ6, БК10-ТФ2, К2-Ф4. Наиболее подходящая комбинация выбирается или из графика Р0=j(С) или интерполяцией. В справочнике [7] уточнена зависимость между P, W, P0 и W0, которая имеет вид P=P0{1-0,022(W-W0)+0,002(W-W0)2}+0,84(W-W0)2, где W0=0,08 для комбинации стекол «крон впереди» и W0=0,21 для комбинации стекол «флинт впереди». При этом для всех аберрационных параметров добавляются индексы «к» или «ф» (Pк, Wк, P0к, W0к и т.д.). Следует иметь ввиду, что в некоторых литературных источниках P0 обозначено как Pmin. Расчет P0 по формуле, приводимой С.В. Трубко, дает значение:
которое отличается от найденного ранее в третьем знаке. Это позволяет утверждать, что при малых значениях Р, W можно пользоваться более простой формулой Г.Г. Слюсарева. Справочник [7] содержит большое количество комбинаций современных марок кроновых и флинтовых стекол, для которых рассчитаны значения P0 (P0к и P0ф) для следующих значений хроматического параметра С: С=±0,006, ±0,004, ±0,002, 0. Расчеты проведены для основной длины волны l0=546,07 нм (e) и дополнительных длин волн l1=480 нм (F¢) и l2=643,8 нм (C¢) Для нас наиболее подходящей оказалась комбинация БК10-ТФ2, для которой получим: С = -0,000763; Р0=-0,350; jk=2,295; Q0=-4,812. г) Определяем значение Q: Q=Q0-(W-W0)/1,67, Q=-4,874. д) Находим значения углов a2 и a3:
Выбранные марки стекол имеют следующие параметры:
a2=0,528, a3=0,335.
е) Определяем толщину линз объектива. Толщину d1 положительной линзы можно определить по формуле d1=0,75Dл2/f ¢+d0, где d0 – толщина линзы по краю. Значение d0 в зависимости от диаметра линзы приведено в табл. 1, причем d1 всегда округляется в сторону увеличения до целого числа. Для примера Dл=20 мм, d0=1,8 мм, тогда d1=
ж) Вычисляем радиусы кривизны поверхностей объектива по известной формуле
Получим r1=54,935 mm; r2=-29,7251 мм; r3=-116,227 мм. Округляя до ближайших целых значения радиусов кривизны в соответствии с ГОСТ 1807-75, примем r1=54,95;
з) Контрольный расчет. Итак, исходный вариант объектива имеет следующие конструктивные параметры:
Расчет объектива выполнялся на основании теории аберраций III порядка, высшие порядки аберраций при этом не учитывались, поэтому объектив может не иметь заданных значений аберраций. Для определения реальных аберраций необходимо выполнить расчет хода осевого и наклонного пучков лучей, воспользовавшись одной из программ (например, «Призма» или «Opal»). В рассматриваемом примере из расчета исходного варианта получены следующие значения аберраций: Ds¢I=0,451 мм, меридиональная кома Dy¢к,I=0,01 мм, хроматизм положения Ds¢l1,l2,I=-0,068 мм. Если остановиться на этом варианте, то остаточные аберрации всей системы монокуляра будут равны разности полученных и заданных аберраций, т.е. Ds¢ост=0,236, Dy¢к,ост = 0,0, Ds¢l1,l2,ост= -0,007. Аберрации телескопической системы после окуляра удобнее оценивать в угловой или в диоптрийной мере [2, 4], причем в диоптриях принято определять продольные аберрации, не зависящие от апертуры (кривизна поля изображения, астигматизм, хроматизм положения). Обозначим аберрацию в угловой мере Ds¢, а аберрацию в диоптриях DL¢. Тогда их значение в угловых минутах можно получить из следующих формул: Ds¢сф=Ds¢ост h1 3438/(f ¢об f ¢ок) =Ds¢ост m¢ 3438/(f ¢ок2); Ds¢к=Dy¢к,ост cos2w¢ 3438/f¢ок. Хроматизм положения рассчитывается при m¢ =0 и правильнее его оценивать в диоптриях: DL¢l1,l2=Ds¢l1,l2,ост 1000/(f ¢ок2) Применяя эти формулы, получим Ds¢сф=5,11¢, Ds¢к=0, DL¢l1,l2= 0,018 дптр.
Оптическая система призменного монокуляра будет давать изображение удовлетворительного качества, если остаточные аберрации в угловой мере не превышают 2-3'; хроматизм положения – 0,25-0,5 дптр; астигматизм и кривизна поля изображения: для обычных окуляров – 3-4 дптр, для широкоугольных – 5-6 дптр; дисторсия: для обычных окуляров – 5-7%, для широкоугольных – до 10%. Хроматическая аберрация увеличения в зрительных трубах допускается до 0,5-1%. Первый вариант объектива дал неудовлетворительный результат из-за наличия сферической аберрации высшего порядка, поэтому расчеты необходимо продолжить. Для перехода ко II варианту расчета необходимо учесть влияние высших порядков сферической аберрации: Ds¢ВП=Ds¢I - Ds¢III =0,451-0,213=0,238; Dy¢к,ВП=Dy¢к,I - Dy¢к, III =0,01 -0,01 =0,0; Ds¢l1,l2,ВП=Ds¢l1,l2,I - Ds¢l1,l2=-0,068+0,061=-0,007. С учетом высших порядков в расчет следует ввести новые значения аберраций: Ds¢н=Ds¢- Ds¢ВП =0,213-0,238 = -0,025; Dy¢к,н=Dy¢к - Dy¢к,ВП =0,01-0,0=0,01; Ds¢l1,l2,н =Ds¢l1,l2 -Ds¢l1,l2,ВП =-0,061 –(-0,007)=-0,054. Тогда Рн=-2Ds¢н f ¢/m2=-2×(-0,025)×80/100=0,04; Wн=W=0,203; Сн=-0,054/80=-0,000675. При переходе к новому варианту можно по значениям Рн, Wн найти новое значение Р0,н =0,04 -0,85×(0,203 –0,1)2=0,031 и подобрать другую пару стекол. Дальнейшие расчеты ведутся по описанной выше методике до получения допустимых остаточных аберраций. Можно выбрать другой путь решения. По найденному новому значению Р0,н находим значение Q, которое может быть получено для ранее выбранной пары стекол БК10-ТФ2 (Р0=-0,350; jk=2,295;
Далее находим новые значения углов:
затем новые значения радиусов кривизны: r1=76,938 mm; r2=-25,966 мм; r3=-72,316 мм и рассчитываем аберрации Ds¢=0,208, Ds¢l1,l2=-0,067, Dy¢к=0,042. Анализ полученных аберраций показывает, что сферическую аберрацию и хроматизм положения удается полностью компенсировать, остаточная кома составляет Dy¢к,ост=0,032, или в угловой мере Ds¢к=0,032×0,8473×3438/20=4,7¢, что можно принять допустимым. Результаты аберрационного расчета объектива должны быть представлены в приложении к расчетно-пояснительной записке и по заданию консультанта может вычерчиваться оптическая схема и сводка аберраций (оптический выпуск).
Качество изображения оптической системы призменного монокуляра можно оценить по результатам суммирования аберраций компонентов [2]. Суммирование аберраций производится также и для того, чтобы определить такое взаимное положение компонентов оптической системы, при котором суммарные аберрации всего прибора в целом будут наименьшими. Для телескопических систем изображение предметов после окуляра лежит в бесконечности, поэтому, как указывалось выше, аберрации следует выражать в угловой мере или в диоптрийной. Несовершенство исправления аберраций телескопической системы характеризуется непараллельностью лучей в выходящих из нее пучках. Аберрацию для данного луча можно уменьшить, если фокальные плоскости объектива и окуляра раздвинуть на величину e>0 или сдвинуть на величину е<0. Но следует помнить, что значения других аберраций при этом могут измениться до недопустимых пределов. Аберрации при наличии расстояния e между фокальными плоскостями объектива и окуляра определяются по следующим формулам: для продольных аберраций в угловой мере:
где для продольных аберраций в диоптриях:
где для поперечных аберраций в угловой мере:
где
Рис.15 Фокальные плоскости не совпадают, е¹0. Определим значение е, при котором Ds¢сф,e=0:
т.е. для получения Ds¢сф,e=0 при Ds¢сф=1¢ фокальные плоскости объектива и окуляра необходимо развести на 0,049 мм. При этом меридиональная кома в угловой мере будет равна Ds¢к= -2,2¢, а хроматизм положения -0,195 дптр. Определим значение е , при котором Ds¢к,e=-1', e=(Ds¢к - Ds¢к,e) f ¢ок / tgs2cos2w¢ 3438=-0,064 мм, т.е. для получения Ds¢к,e=-1' при Ds¢к= -2,2¢ фокальные плоскости необходимо свести на 0,064 мм. При этом сферическая аберрация в угловой мере равна 2,3', а хроматизм положения оказывается переисправленным и равным 0,0875 дптр. Таким образом, при смещении фокальных плоскостей объектива и окуляра вдоль оптической оси, можно балансировать аберрации монокуляра. Точные значения аберраций монокуляра рассчитываются по программам «Призма» или «Opal». По результатам габаритного и аберрационного расчетов вычерчиваются [[8]] оптическая схема (рис. 15) и оптический выпуск (графики аберраций призменного монокуляра).
1. Забелина И.А. Расчет видимости звезд в центре поля зрения оптических приборов. - ОМП, 1978, № 2, с. 21-24. 2. Справочник конструктора оптико-механических приборов. Под общей редакцией В.А. Панова. - Л.: Машиностроение, 1980. -742 с. 3. Проектирование оптико-электронного прибора. Под редакцией В.Н. Дикарева. - М.: изд. МВТУ, 1980. - 68 с. 4. Заказнов Н.П., Кирюшин С.И., Кузичев В.И. Теория оптических систем - 5. Слюсарев Г.Г. Методы расчета оптических систем. - Л.: Машиностроение, 6. Слюсарев Г.Г. Расчет оптических систем. - Л.: Машиностроение, 1975. - 640 с. 7. Трубко С.В. Расчет двухлинзовых склеенных объективов. - Л.: Машиностроение, 1984. - 142 с. 8. Иванова Т.М., Лазарева Н.Л., Лунина И.Н. Оформление конструкторской документации к оптическим изделиям. Учебное пособие. Часть 1. М.: изд. МГТУ, 1999. - 40 с.
приложение 2 (вернуться в текст)
[1] Забелина И.А. Расчет видимости звезд в центре поля зрения оптических приборов. - ОМП, 1978, № 2, с. 21-24. [2] Справочник конструктора оптико-механических приборов. Под общей редакцией В.А. Панова. - Л.: Машиностроение, 1980. -742 с. [3] Проектирование оптико-электронного прибора. Под редакцией В.Н. Дикарева. - М.: изд. МВТУ, 1980. - 68 с. [4] Заказнов Н.П., Кирюшин С.И., Кузичев В.И. Теория оптических систем - М.: Машиностроение, 1992. - 448 с. [5] Слюсарев Г.Г. Методы расчета оптических систем. - Л.: Машиностроение, 1969. - 672 с. [6] Слюсарев Г.Г. Расчет оптических систем. - Л.: Машиностроение, 1975. - 640 с. [7] Трубко С.В. Расчет двухлинзовых склеенных объективов. - Л.: Машиностроение, 1984. - 142 с. [8] Иванова Т.М., Лазарева Н.Л., Лунина И.Н. Оформление конструкторской документации к оптическим изделиям. Учебное пособие. Часть 1. М.: изд. МГТУ, 1999. - 40 с.
Поиск по сайту: |
 4. РАСЧЕТ ОБЪЕКТИВА
4. РАСЧЕТ ОБЪЕКТИВА =-0,353/0,9973=-0,354,
=-0,353/0,9973=-0,354, ;
; .
.
 .
. ,
,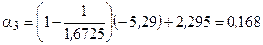 ,
, 5. ОЦЕНКА КАЧЕСТВА ИЗОБРАЖЕНИЯ ОПТИЧЕСКОЙ СИСТЕМЫ ПРИЗМЕННОГО МОНОКУЛЯРА
5. ОЦЕНКА КАЧЕСТВА ИЗОБРАЖЕНИЯ ОПТИЧЕСКОЙ СИСТЕМЫ ПРИЗМЕННОГО МОНОКУЛЯРА ,
,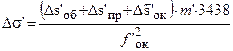 ;
; ,
, ;
; ,
, .
.
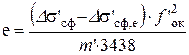 =0,049 мм
=0,049 мм ЛИТЕРАТУРА
ЛИТЕРАТУРА Приложения
Приложения