 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
ОБОСНОВАНИЕ ВЫБОРА ОПТИЧЕСКОЙ СХЕМЫ И ОПРЕДЕЛЕНИЕ ОСНОВНЫХ ОПТИЧЕСКИХ ХАРАКТЕРИСТИКСтр 1 из 5Следующая ⇒
С.И. КИРЮШИН Утверждено редсоветом МВТУ как учебное пособие в 1983 году ГАБАРИТНЫЙ И АБЕРРАЦИОННЫЙ РАСЧЕТ Учебное пособие для курсового проектирования по курсу «Прикладная оптика» В редакции и подготовке электронного варианта принимали участие Крюков А.В., Поспехов В.Г. Москва Данное учебное пособие издается в соответствии с учебным планом.
Рецензенты: к.т.н. доц. ВЗМИ Кахновский В.М. ст. преп. Волков С.В. (с) Московский государственный технический университет им. Н.Э. Баумана ОГЛАВЛЕНИЕ Введение .......................................................................................3 1. Обоснование выбора оптической схемы и определение 2. Габаритный расчет ...................................................................8 3. Определение аберраций объектива ...................................…15 4. Расчет объектива .................................................................…18 5. Оценка качества изображения оптической системы Литература ..............................................................................….26 Приложения .................................................................................27
О замеченных опечатках просьба сообщать по адресу alex_krioukov@mail.ru
Станислав Иванович Кирюшин
ВВЕДЕНИЕ
Если в монокуляре используется одиночная призма, то для получения прямого изображения в приборе она должна иметь крышу. Рассмотрим схемы некоторых призменных монокуляров. Призма Шмидта (рис. 1) позволяет иметь в монокуляре угловое поле не более 8° и образует угол отклонения в 45° между визирной осью (оптической осью в пространстве предметов) и оптической осью окуляра. Монокуляр с призмой Аббе (рис. 2) иногда используется для изготовления призматических биноклей. Призма Пехана (рис. 3) позволяет получить компактную вдоль оси оптическую систему благодаря большой длине хода лучей внутри призмы. Если наблюдательный прибор должен иметь повышенные пластичность и компактность, то следует применять в схеме призму Лемана (рис. 4).
Рис.5
Рис.6
1 - защитное стекло, 2 - головная призма АР-90, 3 - объектив, 4 - башмачная призма с крышей, 5 - клин, 6 - сетка и 7 - окуляр. У монокуляра стереотрубы повышенная перископичность, которая оценивается расстоянием между оптическими осями объектива и окуляра. Разработка оптической системы призменного монокуляра осуществляется в такой последовательности: 1. Обоснование выбора оптической схемы и определение основных характеристик. 2. Габаритный расчет. 3. Выбор или расчет окуляра и призмы и определение аберраций объектива. 4. Расчет объектива. 5. Оценка качества изображения. Основанием для разработки оптической схемы прибора является техническое задание (ТЗ), которое в явном или неявном виде содержит основные характеристики системы, а также требования по достижению определенного качества изображения. Рассмотрим расчет монокуляра на примере.
ОБОСНОВАНИЕ ВЫБОРА ОПТИЧЕСКОЙ СХЕМЫ И ОПРЕДЕЛЕНИЕ ОСНОВНЫХ ОПТИЧЕСКИХ ХАРАКТЕРИСТИК
Таким образом, оптической схемой прибора является схема призменного монокуляра, состоящая из объектива, прямоугольной крышеобразной призмы и окуляра (см. рис. 8). Основными оптическими характеристиками телескопической системы, как известно, являются видимое увеличение Гт, угловое поле 2wи диаметр выходного зрачка D'. Определимих. Видимое увеличение можно выразить через отношение угловых пределов разрешения в пространстве изображений (y¢) и в пространстве предметов (y):
Угловой предел разрешения y' определим исходя из указаний о необходимости иметь впечатление от изображения минимального отклонения не хуже, чем от миллиметровых делений, т.е. y'=1/250=0,004 или y'=13,3', где 250 мм – расстояние наилучшего зрения. Угловой предел разрешения y в пространстве предметов (см. рис. 8) равен y=DА/Н, где DА – минимальное горизонтальное отклонение, равное 3 м, Н – высота полета, т.е.y=3/3000=0,001 или y=3,3' *). ___________________________________________________________________________________________________________ *) Если принять y'=1' и Гт=1х (т.е. допустить, что прибор не нужен), то условия наблюдения будут дискомфортными, так как наблюдатель будет видеть изображение смещения в 3 м как перемещение точки размером примерно в 0,1 мм на такую же величину. Видимое увеличение вычислим по формуле (1) Гт=13,3/3,3=4х. Следует помнить, что призма с крышей имеет Гпр=-1х, поэтому при расчете зрительной трубы следует принимать Гт=-4х. Угловое поле 2w зависит от линейного поля 2y=600 м и высоты Н=3 км, tgw=y/H, откуда tgw=0,1, w=5,71°. Примем 2w=12°. Для определения диаметра выходного зрачка воспользуемся [[1]] зависимостью диаметра зрачка глаза от яркости фона, из которой следует, что при Lv,Ф =0,45 кд/м2 Dгл=5 мм. Считая, что D'=Dгл, примем D'=5 мм, так как D=ГтD' и следовательно, D=20 мм. Тогда ожидаемый угловой предел разрешения [[2]] yож=140''/D будет равен yож=7", что позволяет прибору иметь линейный предел разрешения в пространстве предметов значительно выше требуемого (d=3 м; dож=0,16 м). Условия наблюдения зависят не только от разрешающей способности прибора, но и от контраста К, оптимальное значение которого 0,6-0,95:
Определим яркость предмета Lv,прс коэффициентом диффузного отражения r=0,6 (покрытие самолета, вертолета [[3]]) при условии, что на его поверхности создана освещенность на порядок меньше, чем на поверхности Земли при восходе или заходе Солнца [3], т.е. Еv,пр=10¸50 лк. В соответствии с формулой Lv,пр=r Ev,пр/p, Lv,пр=1,9¸9,6 кд/м2, а по формуле (2) получим К=0,76¸0,95, что позволяет сделать вывод об оптимальных условиях наблюдения и с энергетической точки зрения. Итак, необходимо рассчитать оптическую систему призменного монокуляра, имеющего: Гт=4х; 2w=12°; D'=5 мм; L=100 мм (L=f'об+f'ок); Kw=0,5.
ГАБАРИТНЫЙ РАСЧЕТ
Для удобства расчета оптическую схему (рис. 10) монокуляра развернем по горизонтальной оси и заменим призму эквивалентной пластинкой *). На рис. 10 показаны осевой и наклонный пучки лучей, рассмотрение хода которых позволяет провести габаритный расчет. Для уменьшения размеров монокуляра, главным образом призмы, и достижения лучшего качества изображения на краю поля из всего наклонного пучка лучей, поступающего во входной зрачок под наибольшим углом w1, через систему пропускают только часть его, симметричную относительно главного луча. Ширина этой части наклонного лучка во входном зрачке измеряется величиной 2m1=Kw D, где D – диаметр входного зрачка, a Kw – коэффициент виньетирования, который в нашем примере равен 0,5. Габаритный расчет проводится в следующем порядке: 1. Определение углового поля окуляра 2w' tgw¢=Гт tgw, tgw¢= -4·(-0,105) = 0,42, 2w¢=45,6°. 2. Определение фокусного расстояния окуляра f'ок Фокусное расстояние окуляра определяется по формуле, найденной из совместного решения известных уравнений:
f'ок= 100 / [1–(–4)] = 20 мм. 3. Определение фокусного расстояния объектива f'об f'об= – Гт f'ок , f'об= – (–4) 20= 80 мм.
Поиск по сайту: |
 Призменным монокуляром называется прибор, оптическая система (ОС) которого представляет собой простую зрительную трубу с призмой или системой призм для перевертывания изображения, благодаря чему весь прибор создает прямое изображение.
Призменным монокуляром называется прибор, оптическая система (ОС) которого представляет собой простую зрительную трубу с призмой или системой призм для перевертывания изображения, благодаря чему весь прибор создает прямое изображение. Призменный монокуляр применяется и как самостоятельный прибор (буссоль, перископы и т.п.), и как составная часть стереоскопических наблюдательных систем (дальномеры, стереотрубы).
Призменный монокуляр применяется и как самостоятельный прибор (буссоль, перископы и т.п.), и как составная часть стереоскопических наблюдательных систем (дальномеры, стереотрубы).

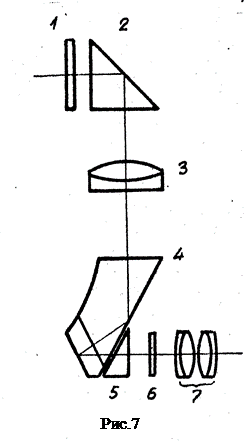 На рис. 5 и 6 показаны оптические схемы монокуляров с призменными системами О.Н. Малафеева (соответственно I и II рода, в иностранной литературе известных как системы Порро). Особенностью этих схем является то, что оптические оси объектива и окуляра не лежат в одной плоскости. Приведенная на рис. 7 оптическая схема монокуляра стереотрубы включает следующие элементы:
На рис. 5 и 6 показаны оптические схемы монокуляров с призменными системами О.Н. Малафеева (соответственно I и II рода, в иностранной литературе известных как системы Порро). Особенностью этих схем является то, что оптические оси объектива и окуляра не лежат в одной плоскости. Приведенная на рис. 7 оптическая схема монокуляра стереотрубы включает следующие элементы: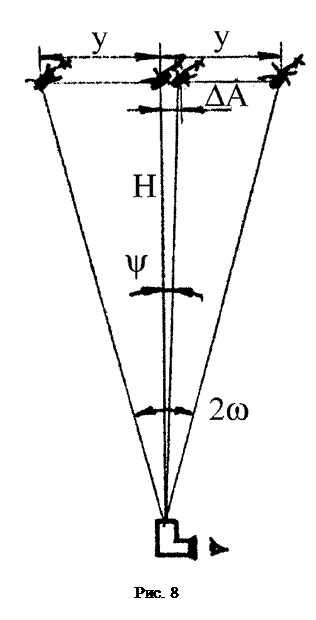 Техническое задание. Рассчитать оптическую систему прибора, предназначенного для наблюдения за перемещениями вертолета, находящегося в зените на высоте 3 км. Вертолет будет отклонятьсяот вертикали в горизонтальном направлении не более чем на 300 м (рис. 8). Прибор должен позволять заметить отклонение вертолета в 3 м, причем впечатление от изображения этого минимального отклонения должно быть не хуже, чем от миллиметровых делений линейки. Наблюдения проводятся в сумеречное время (восход, заход Солнца) при ожидаемой минимальной яркости фона (небо, облака) LV,Ф=0,45 Кд/м2. Допускается падение освещенности на краю поля вдвое. Зрительная ось оператора должна быть горизонтальной. Длина оптической системы L=100 мм.
Техническое задание. Рассчитать оптическую систему прибора, предназначенного для наблюдения за перемещениями вертолета, находящегося в зените на высоте 3 км. Вертолет будет отклонятьсяот вертикали в горизонтальном направлении не более чем на 300 м (рис. 8). Прибор должен позволять заметить отклонение вертолета в 3 м, причем впечатление от изображения этого минимального отклонения должно быть не хуже, чем от миллиметровых делений линейки. Наблюдения проводятся в сумеречное время (восход, заход Солнца) при ожидаемой минимальной яркости фона (небо, облака) LV,Ф=0,45 Кд/м2. Допускается падение освещенности на краю поля вдвое. Зрительная ось оператора должна быть горизонтальной. Длина оптической системы L=100 мм.
 Естественно, что для наблюдения за удаленным объектом необходима телескопическая система, состоящий как минимум из объектива и окуляра. Для согласования направления на объект и горизонтального расположения зрительной оси оператора необходима отражательная призма с углом отклонения 90°. А так как изображение должно быть прямым (важно правильно оценивать направление перемещений вертолета), призму снабжают крышей.
Естественно, что для наблюдения за удаленным объектом необходима телескопическая система, состоящий как минимум из объектива и окуляра. Для согласования направления на объект и горизонтального расположения зрительной оси оператора необходима отражательная призма с углом отклонения 90°. А так как изображение должно быть прямым (важно правильно оценивать направление перемещений вертолета), призму снабжают крышей. .
.
 ,
,