 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Пример 6.3.6-2. Выполнить интерполяцию таблично заданной функции по методу Лагранжа
Преимущество этой формулы в том, что число и расположение узловых точек могут быть любыми (в том числе неравномерными).
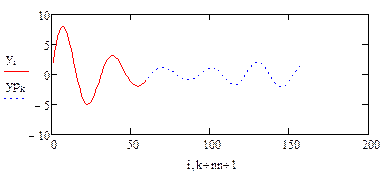
Помимо вычисления значений функций в пределах интервала данных все рассмотренные ранее функции могут осуществлять экстраполяцию (прогнозирование поведения функции за пределами интервала заданных точек) с помощью зависимости, основанной на анализе расположения нескольких исходных точек на границе интервала данных. В Mathcad имеется и специальная функция предсказания predict(Y, m, n), где Y – вектор заданных значений функции, обязательно взятых через равные интервалы аргумента, а m – число последовательных значений Y, на основании которых функция predict возвращает n значений Y. Значений аргумента для данных не требуется, поскольку по определению функция действует на данных, идущих друг за другом с одинаковым шагом. Функция использует линейный алгоритм предсказания, который точен, когда экстраполируемая функция гладкая. Функция может быть полезна, когда требуется экстраполировать данные на небольшие расстояния. Вдали от исходных данных результат чаще всего оказывается неудовлетворительным. Пример 6.3.6-3. Задан массив из 60 точек На основании первых m точек провести экстраполяцию (предсказание) значений n точек.
MathCad имеется три сплайн-функции: · cspline( ) · pspline( ) · lspline( ) Эти функции возвращают вектор коэффициентов вторых производных, который мы будем называть S. Этот вектор Эти три функции отличаются только граничными условиями: · функция lspline( ) генерирует кривую сплайна, которая приближается к прямой линии в граничных точках; · функция pspline( ) генерирует кривую сплайна, которая приближается к параболе в граничных точках. · функция cspline( ) генерирует кривую сплайна, которая может быть кубическим полиномом в граничных точках. · interpвозвращает интерполируемое значение, соответствующее аргументу Вектор
Пример 6.3.6-4. Пусть значения функции, полученные в ходе эксперимента, представлены в виде таблицы:
Поиск по сайту: |
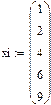
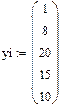
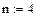
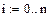
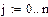
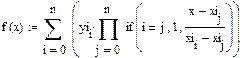
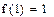
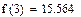
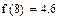
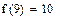
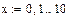
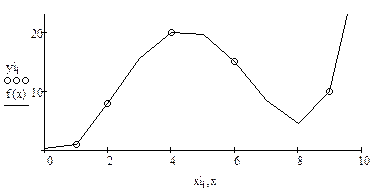
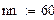
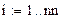
 .
.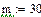
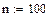
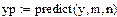
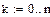
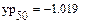
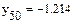


 обычно используется в функции interp( ), описанной ниже. Аргументы должны быть вещественными векторами одинаковой длины. Значения вектора
обычно используется в функции interp( ), описанной ниже. Аргументы должны быть вещественными векторами одинаковой длины. Значения вектора  должны быть расположены в порядке возрастания.
должны быть расположены в порядке возрастания. .
.  одной из функций pspline( ), lspline( ) илиcspline( ).
одной из функций pspline( ), lspline( ) илиcspline( ).