|
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Интерполяционная формула ЛагранжаСтр 1 из 5Следующая ⇒
Тема 6.3. Интерполяция функций
6.3.1. Постановка задачи 6.3.2. Интерполяционная формула Лагранжа 6.3.3. Интерполяционные формулы Ньютона 6.3.3.1. Конечные разности 6.3.3.2. Первая интерполяционная формула Ньютона 6.3.3.3. Вторая интерполяционная формула Ньютона 6.3.4. Сплайн – интерполяция 6.3.5. Сравнение интерполяционных многочленов по применению 6.3.6. Технология интерполяции функций в среде математических пакетов 6.3.6.1. Технология интерполяции функций в среде системы MathCad 6.3.6.2. Технология интерполяции функций в среде MatLab 6.2.7. Тестовые задания по теме «Интерполяция функций»
Постановка задачи
Вычисление значений функции y = f(x) – одна из тех задач, с которой приходится постоянно сталкиваться в инженерной практике. Однако сделать это не всегда возможно. Примером тому следующие типичные ситуации: · функция задана таблицей значений (нет аналитического выражения) · аналитическое выражение f(x) есть, но получение ее значений затруднено громоздкими и сложными вычислениями; · значения функции в требуемых точках могут быть получены только экспериментально.
В этих и ряде других случаев возникает необходимость приближенного вычисления функции y = f(x). Задача аппроксимациисостоит в следующем. Функцию f(x), заданную таблично, требуется приближенно заменить (аппроксимировать) некоторой функцией j(х) так, чтобы отклонение j(х) от f(x) в некоторой области удовлетворяло заданному условию. Функция j(х) называется аппроксимирующейфункцией. В качестве аппроксимирующей функции часто используют алгебраический многочлен вида:
jm(x) = a 0 + a 1 x + a 2 x2 + … + a m xm . (6.3.1-1)
В этом случае говорят о параболической аппроксимации. Частным случаем задачи аппроксимации таблично заданной функции является интерполирование. Интерполирование состоит в следующем. Для функции y = f(x), заданной в (n + 1) точке
Будем называть (6.3.1-2) условием интерполяции, точки При интерполяции критерием приближения аппроксимирующей функции к заданной является совпадение их значений в узлах интерполяции. Геометрической интерпретацией задачи интерполяции является нахождение функции, график которой проходит через заданную систему точек
Рис.6.3.1-1
Применяя интерполирующую функцию (6.3.1-1), запишем условие (6.3.1-2) для каждого из (n + 1) узлов. В результате получим следующую систему (n + 1) линейных уравнений:
Эта система однозначно разрешима, так как ее определитель (определитель Вандермонда) отличен от нуля, если узлы интерполяции различны. Решение полученной системы n+1 линейных уравнений относительно неизвестных а0, а1, …, аn позволяет найти коэффициенты интерполирующего многочлена (6.3.1-1).
Пример 6.3.1-1.Пусть функция y = f(x) задана таблично:
Требуется построить интерполяционный многочлен, позволяющий вычислить значение f(x) в точке x = 1.43. Полагая x0 = 1.2 , x1 = 1.4 , x2 = 1.6, y0 =-0.16, y1 = -0.24, y2 = -0.24, получим систему уравнений
Решая систему уравнений, получим следующие значения а0 = 2, а1 = -3, а2 = 1.Тогда интерполяционный многочлен имеет следующий вид: P2(x) = 2 – 3x + x2, а значение многочлена в точке 1.43 равно P2(1.43) = - 0.2451.
Интерполяционная формула Лагранжа
Пусть функция f(x) задана в (n + 1) узлах, произвольно расположенных на отрезке [a;b]: y0 = f(x0), y1 = f(x1), … yn = f(xn). Требуется найти интерполирующий алгебраический многочлен Ln(x), степени не выше n, удовлетворяющий условию (6.3.1-2), такой, что:
L0 = y0, L1 = y1, …, Ln = yn. (6.3.2-1)
Будем искать Ln(x) вида:
Ln = Q0(x)y0 + Q1(x)y1 + … + Q n(x) yn, (6.3.2-2)
где Qi(x) – коэффициенты, зависящие только от узлов Для того чтобы выполнялись условия интерполяции (6.3.2-1), требуется, чтобы коэффициенты Qi(x) удовлетворяли условию:
Действительно, чтобы L(х0)=y0, необходимо, чтобы в (6.3.2-2) Q0(x0) = 1, Q1(x0) = 0, …, Qn(x0)= 0.
В то же время в других узлах интерполяции первое слагаемое формулы 6.3.2-2, связанное с yi, должно быть равно нулю, то есть: Q0(xi) = 0, i = 1, 2, … , n. Этим требованиям отвечает коэффициент вида:
Поскольку в числителе Q0(x) записано произведение разностей со всеми узлами кроме х0, то Q0(x) обращается в ноль при х = хi ; i = 1, 2, … , n. В то же время при х = х0числитель и знаменатель дроби взаимно сокращаются и Q0(x0)=1. Для того чтобы Ln(x1) = y1, коэффициенты в (6.3.2-2) должны принять значения: Q1(x1) = 1; Q0(x1) = 0… Qn(x1) = 0. Чтобы в других узлах коэффициент Q1(x), связанный с yi, принял значение ноль, нужно, чтобы Q1(xi) = 0, i = 0, 2, 3, …, n. Тогда произведение разностей в числителе обращается в ноль во всех узлах, кроме х1, а при х = х1 коэффициент равен 1. Обобщая сказанное выше, получим выражение для Qi(x):
Для интерполяционного многочлена Лагранжа это выражение будет следующее:
Несмотря на громоздкость (6.3.2-5), одним из преимуществ формулы Лагранжа является возможность ее записи непосредственно по заданной таблице значений функции. Для этого следует учесть следующее правило: формула содержит столько слагаемых, сколько узлов в таблице; каждое слагаемое – это произведение дробного коэффициента на соответствующее значение yi; числитель коэффициента при yi содержит произведение разностей х со всеми узлами кроме Используя приведенные правила, получим формулы Лагранжа для двух узлов (n=1) - линейная интерполяция:
для трех узлов (n=2) - квадратичная интерполяция:
Оценку погрешности формулы Лагранжа определяют исходя из приближенного равенства
где m– число узлов, используемое в формуле.
Для того, чтобы уменьшить погрешность интерполяции, используется прием перенумерации узлов исходной таблицы, последовательно выбирая в качестве х0, Схемы алгоритма интерполяции с помощью формул Лагранжа приведены на
Рис. 6.3.2-1. Схема алгоритма интерполяции по формуле Лагранжа
Рис. 6.3.2-2. Схема алгоритма процедуры-функции LX( ) вычисления многочлена Лагранжа к-ой степени в точке xl Пример 6.3.2-1. Пусть функция y = f(x) задана таблично:
Требуется с использованием формулы Лагранжа вычислить значение f(x) в точке x = 1.45. Перенумеруем узлы:
x0 = 1.4 y0 =-0.24 x1 = 1.6 y1 = -0.24 x2 = 1.2 y2 = -0.16 х3 = 1.8 y3 = -0.16 x4 = 1.0 y4 = 0.0 . Для приближенного вычисления значения функции воспользуемся формулами линейной и квадратичной интерполяции: При n + 1 = 2 используем узлы x0 и x1
При n +1 = 3 используем узлы x0 , x1 и x2
Для оценки погрешности используем соотношение
Если полученная величина соответствует заданной погрешности (например, e=0.1), то вычисления прекращают. Если e<Rn, то количество узлов увеличивают. Вычисления повторяют до тех пор, пока не выполнится условие Rn ≤ e. Если, в соответствии с условиями поставленной задачи, требуется найти значения функции не в одной, а в нескольких точках, то рекомендуется провести преобразования формулы и получить многочлен в явном виде (Пример 6.3.1-1). Если в формуле были использованы все точки, заданные таблицей, то оценить погрешность не представляется возможным.
Поиск по сайту: |
 ,(i = 0, 1, 2,…, n), необходимо вычислить значения функции в точках, не совпадающих с табличными;
,(i = 0, 1, 2,…, n), необходимо вычислить значения функции в точках, не совпадающих с табличными; , найти функцию j(х), принимающую в этих точках заданные значения, то есть
, найти функцию j(х), принимающую в этих точках заданные значения, то есть ,i = 0, 1, 2, … n. (6.3.1-2)
,i = 0, 1, 2, … n. (6.3.1-2) , i = 0, 1, …, n (рис. 6.3.1-1). Если в качестве интерполирующей функции используется алгебраический многочлен
, i = 0, 1, …, n (рис. 6.3.1-1). Если в качестве интерполирующей функции используется алгебраический многочлен 
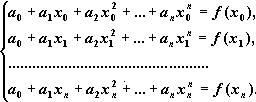

 , i=0,1, …,n и текущего значения х.
, i=0,1, …,n и текущего значения х.
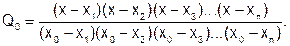 (6.3.2-3)
(6.3.2-3)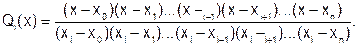 (6.3.2-4)
(6.3.2-4) . (6.3.2-5)
. (6.3.2-5)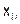 а знаменатель полностью повторяет числитель при х =
а знаменатель полностью повторяет числитель при х = 
 (6.3.2-6)
(6.3.2-6)


 .
.