 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Вторая интерполяционная формула Ньютона
Вторая формула Ньютона обладает аналогичными свойствами относительно левой части таблицы. Для ее построения используют многочлен вида:
Pn(x)=a0 + a1(x-xn) + a2(x-xn)(x-xn-1) + …+ an(x-xn)(x-xn-1)…(x-x1), (6.3.3-8)
где аi, i = 0, 1, 2, …, n – коэффициенты, не зависящие от узлов интерполяции. Для определения коэффициентов аi будем в (6.3.3-8) поочередно подставлять узлы интерполяции. При х = xn Pn(xn) = yn, следовательно, a0 = yn. При х = xn-1 имеем Pn(xn-1) = yn-1 = a0 + a1(xn-1-xn) = yn + a1(xn-1-xn), откуда
Продолжая подстановку, получим выражение для всех коэффициентов многочлена (6.3.3-8) и запишем вторую интерполяционную формулу Ньютона:
Введя обозначение: и, подставив х в (6.3.3-8), получаем формулу Ньютона для интерполяции назад:
Воспользуемся этой формулой для вычисления значения функции, заданной таблицей 6.3.3-1, в точке х = 1.7. Точка х=1.7 расположена в конце таблицы. В качестве узлов интерполяции выберем:х3=1.8, х2=1.6 и х1=1.4:
Погрешности интерполяционных формул Ньютона определяются соотношением:
· для первой формулы Ньютона:
· для второй формулы Ньютона:
где На практике, если интерполируемая функция y = f(x) задана таблично, полагая, что Dn+1 = const, а h –достаточно мало, используют приближенные равенства:
Пример 6.3.3-1. Вычислить c использованием 1-й и 2-й формул Ньютона значение функции, заданной таблицей равноотстоящих узлов, в точке х=1.23.
Используем 1-ю формулу Ньютона. Выберем х0 = 1.2; х1 = 1.3; х2= 1.4. Построим таблицу конечных разностей:
Тогда:
Практическая погрешность оценивается соотношением:
e1 = |Р2(х) - Р1(х)|=|0.206958-0.206335|=0.000623. Решим ту же задачу с помощью 2-й формулы Ньютона. Пусть хn = 1.3; хn-1 = 1.2; хn-2= 1.1. Таблица конечных разностей имеет вид:
Тогда:
В последние годы интенсивно развивается новый раздел современной вычислительной математики – теория сплайнов. Сплайны позволяют эффективно решать задачи обработки экспериментальных зависимостей между параметрами, имеющими достаточно сложную структуру. Рассмотренные выше методы локальной интерполяции, по существу, являются простейшими сплайнами первой степени (для линейной интерполяции) и второй степени (для квадратичной интерполяции). Наиболее широкое практическое применение, в силу их простоты, нашли кубические сплайны. Основные идеи теории кубических сплайнов сформировались в результате попыток математически описать гибкие рейки из упругого материала (механические сплайны), которыми издавна пользовались чертежники в тех случаях, когда возникала необходимость проведения через заданные точки достаточно гладкой кривой. Известно, что рейка из упругого материала, закрепленная в некоторых точках и находящаяся в положении равновесия, принимает форму, при которой ее энергия является минимальной. Это фундаментальное свойство позволяет эффективно использовать сплайны при решении практических задач обработки экспериментальной информации. В общем случае для функции y = f(x) требуется найти приближение y = S(x) таким образом, чтобыf(xi) = S(xi) в точках x = xi, a в остальных точках отрезка [a;b] значения функций f(x) и S(x) были близкими между собой. При малом числе экспериментальных точек для решения задачи интерполяции можно использовать один из методов построения интерполяционных полиномов. Однако при большом числе узлов интерполяционные полиномы становятся практически непригодными. Это связано с тем, что степень интерполяционного полинома лишь на единицу меньше числа экспериментальных значений функций. Можно, конечно, отрезок, на котором определена функция, разбить на участки, содержащие малое число экспериментальных точек, и для каждого из них построить интерполяционные полиномы. Однако в этом случае аппроксимирующая функция будет иметь точки, где производная не является непрерывной, т. е. график функции будет содержать точки “излома”. Кубические сплайны лишены этого недостатка. Исследования показали, что гибкая тонкая линейка между двумя узлами достаточно хорошо описывается кубическим полиномом, и поскольку она не разрушается, то аппроксимирующая функция должна быть, по меньшей мере, непрерывно дифференцируемой.
Таким образом, сплайн– это функция, которая на каждом частичном отрезке интерполяции является алгебраическим многочленом, а на всем заданном отрезке непрерывна вместе с несколькими своими производными. Пусть интерполируемая функция f(x)задана своими значениями yi, в узлах хi,
где Потребуем совпадения значений S(x)в узлах с табличными значениями функции f(x):
Число этих уравнений (2n) в два раза меньше числа неизвестных коэффициентов. Для того чтобы получить дополнительные условия, потребуем также непрерывности первой и второй производных сплайна во всех точках, включая узлы. Для этого следует приравнять левые и правые производные S'(x–0), S'(x+0), S"(x–0), S"(x+0) во внутреннем узле xi. Вычислим выражения для производных S'(x), S"(x)последовательным дифференцированием (6.3.4-1):
S'(x) = bi + 2ci(x–xi-1) + 3di(x–xi-l)2, (6.3.4-4)
S''(x) = 2ci + 6di(x–xi-l),(6.3.4-5)
найдем правые и левые производные в узле:
S'(xi–0) = bi + 2сhi + 2dihi,
S'(xi+0) = bi+1, где i = 1,2,..., n -1.
Аналогично поступаем для второй производной:
S"(x–0) = 2ci+6dihi,
S"(х+0) = 2сi+1.
Приравняв левые и правые производные, получаем:
bi+1= bi+2cihi+2dihi2 (6.3.4-6)
сi+1 = сi- + 3dihi, где i = 0, 1,..., n–1. (6.3.4-7)
Уравнения (6.3.4-6), (6.3.4-7) дают еще 2(n–1) условий. Для получения недостающих уравнений накладывают требования к поведению сплайна на концах отрезка интерполяции. Если потребовать нулевой кривизны сплайна на концах отрезка интерполяции (т. е. равенство нулю второй производной), то получим:
сi=0, cn+3dnhn = 0. (6.3.4-8)
Исключив из уравнений (6.3.4-2) – (6.3.4-3) nнеизвестных ai, получаем систему уравнений:
где i=0, 1,...., n - 1. Система (6.3.4-9) состоит из 3(n-1)уравнений. Решив систему (6.3.4-9), получаем значения неизвестных bi, ci, di,определяющих совокупность всех формул для искомого интерполяционного сплайна:
Программа, реализующая метод сплайн-интерполяции, достаточно громоздка, поэтому ограничимся обсуждением решения задачи об интерполяции синуса с помощью сплайнов, используя функции пакетов п.п. 6.3.6.
Поиск по сайту: |
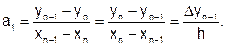
 (6.3.3-9)
(6.3.3-9)
 (6.3.3-10)
(6.3.3-10)
 (6.3.3-11)
(6.3.3-11) (6.3.3-12)
(6.3.3-12) - некоторое промежуточное значение между узлами интерполяции.
- некоторое промежуточное значение между узлами интерполяции. (6.3.3-13)
(6.3.3-13)



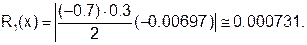
 (6.3.4-1)
(6.3.4-1) — четверка неизвестных коэффициентов. Можно доказать, что задача нахождения кубического сплайна имеет единственное решение.
— четверка неизвестных коэффициентов. Можно доказать, что задача нахождения кубического сплайна имеет единственное решение. (6.3.4-2)
(6.3.4-2) (6.3.4-3)
(6.3.4-3) (6.3.4-9)
(6.3.4-9) где i = 0,1,...,n–1.(6.3.4-10)
где i = 0,1,...,n–1.(6.3.4-10)