 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Раскрытие неопределенностей по правилу Лопиталя ⇐ ПредыдущаяСтр 4 из 4
Неопределенности
Раскрытие неопределенностей
Пример 1. Вычислить Решение. При
По формуле (4) данный предел тоже равен Пример 2.
Замечание 1. В некоторых случаях, после применения формулы (4), отношение производных может оказаться неопределенностью Замечание 2. В целях сокращения вычислений рекомендуется правило Лопиталя применять в сочетании с другими приемами раскрытия неопределенностей.
Пример 3.
Получили предел произведения двух функций. Вычислим их отдельно. Предел второго сомножителя приводит к неопределенности
По теореме о пределе произведения исходный предел равен 0. Пример 4. Вычислить Применение правила Лопиталя приводит к сложному выражению. Проще поступить так. При Тогда
Таким образом, в данном примере мы использовали эквивалентность б.м. и повторное применение правила Лопиталя. Неопределенности
Пример 5. Решение. Неопределенность
Тогда
Пример 6. Решение. Есть неопределенность
При
Тогда
Заключение. Мы рассмотрели некоторые приемы вычисления пределов функций одной переменной. Основное внимание при этом было уделено раскрытию неопределенностей различными методами. Существуют и другие, более тонкие методы раскрытия неопределенностей, не рассмотренные в настоящей работе. С ними вы сможете ознакомиться по книгам, список которых приведен выше. Мы, считаем нужным отметить, что для овладения практикой вычисления пределов необходимо значительное количество упражнений. С этой целью к методическим указаниям приложены варианты контрольных работ. Задачи каждого варианта решить при следующих условиях: 1 – вычислить пределы с помощью алгебраических преобразований; 2 – вычислить пределы с помощью замечательных пределов; 3 – найти пределы, используя эквивалентные бесконечно малые; 4 – раскрыть неопределенности по правилам Лопиталя (при необходимости использовать другие приемы).
Поиск по сайту: |
 . Если функции f(x) иф(x) дифференцируемые в окрестности точки a и являются бесконечно малыми (бесконечно большими) при
. Если функции f(x) иф(x) дифференцируемые в окрестности точки a и являются бесконечно малыми (бесконечно большими) при 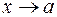 , то из существования предела
, то из существования предела  следует существование
следует существование  , причем
, причем (4).
(4). .
. числитель и знаменатель дроби стремятся к нулю, мы имеем неопределенность
числитель и знаменатель дроби стремятся к нулю, мы имеем неопределенность 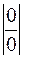 . Рассмотрим предел отношения производных:
. Рассмотрим предел отношения производных: .
. .
. , т.к.
, т.к. 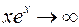 при
при  .
. . Тогда правило Лопиталя применяют еще раз, т.е. переходят к пределу отношения производных второго порядка.
. Тогда правило Лопиталя применяют еще раз, т.е. переходят к пределу отношения производных второго порядка.
 .
.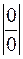 . Чтобы ее раскрыть, применим правило Лопиталя повторно:
. Чтобы ее раскрыть, применим правило Лопиталя повторно: .
. .
. ,
,  , тогда
, тогда  .
.

 .
. . Для применения правила Лопиталя к раскрытию этих неопределенностей путем тождественных преобразований необходимо их свести к неопределенности
. Для применения правила Лопиталя к раскрытию этих неопределенностей путем тождественных преобразований необходимо их свести к неопределенности  .
. . Данное выражение представим в виде
. Данное выражение представим в виде  и вычислим отдельно предел показателя степени:
и вычислим отдельно предел показателя степени:
 .
. .
.
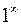 , т.к.
, т.к.  при
при  .
. , поэтому
, поэтому  при
при 

 .
. .
.