 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Применение эквивалентных бесконечно малых
Бесконечно малые Теорема. Пусть функции
Из этой теоремы следует, что если при
Эти равенства означают, что при вычислении пределов множители в числителе или в знаменателе можно заменить на эквивалентные Приведем некоторые пары эквивалентных бесконечно малых величин
Пример 1. Вычислить Решение. Функции Тогда
При помощи замены б.м. на эквивалентную удается очень быстро преодолеть те искусственные , иногда громоздкие преобразования, которые нами использовались при раскрытии неопределенностей другими способами. Чтобы убедиться в этом, вернемся к примеру 3, п.3 и вычислим его с помощью эквивалентных б.м. . При
Преимущества использования бесконечно малых очевидны.
Пример 2. Вычислить Решение. Обозначим
Метод замены переменной, использованный в данном примере, значительно расширяет возможности применения эквивалентных б.м. величин. Замечание. Не рекомендуется заменять под знаком предела слагаемые на эквивалентные им величины. Например, при
В действительности все обстоит по-другому:
Рассмотренные примеры связаны с неопределенностью
Пример 3. Вычислить Решение. Неопределенность
При
Пример 4. Вычислить При
Т.к. при Тогда
В зависимости от возможных значений показателя степени функции
Поиск по сайту: |
 и
и 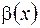 называются эквивалентными при
называются эквивалентными при 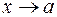 , если
, если 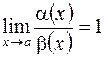 Обозначается эквивалентность так:
Обозначается эквивалентность так: 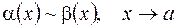 . Применение эквивалентных б.м. является очень эффективным способом раскрытия неопределенностей. В основе следующая теорема.
. Применение эквивалентных б.м. является очень эффективным способом раскрытия неопределенностей. В основе следующая теорема. являются эквивалентными при
являются эквивалентными при 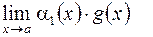 , то существует
, то существует 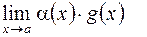 , причем
, причем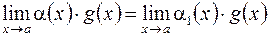 . (3)
. (3)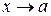
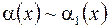 ,
,  , то
, то 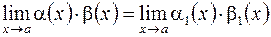 ;
;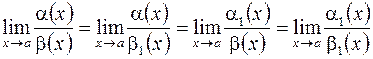 .
. ;
;  ;
;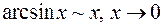 ;
;  ;
;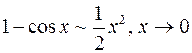 ;
; 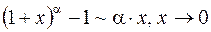 .
.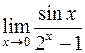 .
.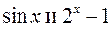 являются б.м. при
являются б.м. при  , заменим их эквивалентными б.м.:
, заменим их эквивалентными б.м.:  , при
, при 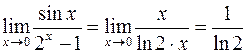 .
.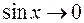 , поэтому
, поэтому 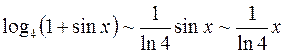 ; бесконечно малая
; бесконечно малая 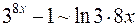 . Тогда
. Тогда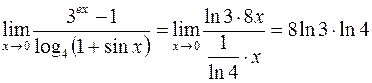 .
.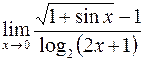 .
.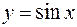 и заметим, что при
и заметим, что при 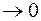 . Тогда
. Тогда 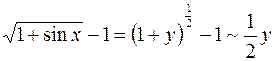 при
при 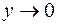 , т.е.
, т.е. 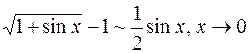 . При
. При  . Тогда
. Тогда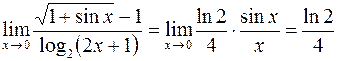 .
. ;
; 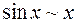 . Если перейти к эквивалентным функциям в примере
. Если перейти к эквивалентным функциям в примере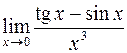 , то получим
, то получим  .
.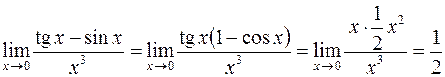 .
.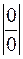 , но эквивалентные б.м. можно использовать при раскрытии и других неопределенностей.
, но эквивалентные б.м. можно использовать при раскрытии и других неопределенностей.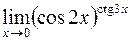 .
.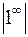 . Применим следующие преобразования:
. Применим следующие преобразования: .
. , тогда
, тогда 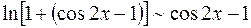 . В свою очередь,
. В свою очередь,  . Поэтому
. Поэтому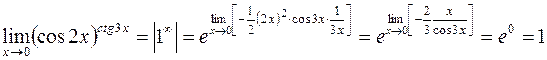 .
. , где
, где 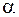 - произвольное положительное число.
- произвольное положительное число. данный предел можно вычислить путем умножения и деления на сопряженное выражение. Для других значений
данный предел можно вычислить путем умножения и деления на сопряженное выражение. Для других значений 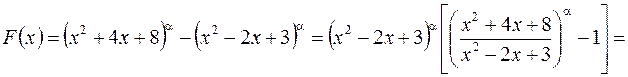
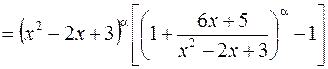 .
.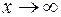
 , то
, то  .
.
 .
.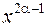 ведет себя по-разному при
ведет себя по-разному при  . Если
. Если  , то
, то  . Тогда искомый предел равен 0. Если
. Тогда искомый предел равен 0. Если  , то он равен
, то он равен 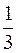 , и наконец, если
, и наконец, если 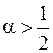 , то
, то  , предел равен
, предел равен 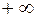 .
.