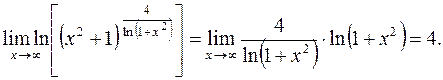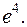|
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Простейшие приемы раскрытия неопределенностей
Читатель, знакомый с понятием неопределенности, обратил внимание на то, что почти все примеры, рассмотренные выше, относятся именно к этому случаю. Это объясняется тем, что основные сложности при вычислении пределов как раз связаны с раскрытием неопределенностей; пределы, вычисляемые по формуле (1) или с использованием арифметических операций над пределами, с точки зрения совершенства техники вычисления пределов, интереса не представляют. Рассмотрим сначала неопределенности Напомним, что неопределенностью Заметим, что если одна из функций при Условно это обстоятельство записывают так:
Пример 1. Вычислить Решение. При
Пример 2.Вычислить Решение. Значение = Пример 3.Вычислить Решение. Имеем неопределенность ( воспользовались равенством
По теореме о пределах произведения искомой предел равен
Пример 5.
Пример 6.Вычислить Решение. Неопределенность
при Приводя к общему знаменателю, получим:
Перейдем к рассмотрению неопределенностей других видов. Неопределенность
Пример 7.
Пример 8.Вычислить Решение. Т.к.
Неопределенность
Пример 9. Решение. Основание
Тогда
Обозначим выражение
Пример 10. Решение. В данном примере тоже имеем неопределенность Воспользуемся формулой (2):
Неопределенность
Пример 11. Решение. Выражение
По такой же схеме раскрывается и неопределенность В целях упрощения соответствующих выкладок рекомендуется выражения предварительно прологарифмировать. Пусть
Пример 12. Решение. Неопределенность вида
Следовательно, исходный предел равен
Поиск по сайту: |
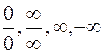 .
.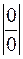 называется
называется 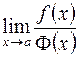 , когда
, когда 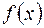 и
и  являются, бесконечно малыми при
являются, бесконечно малыми при 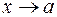 (а может быть конечным числом, или
(а может быть конечным числом, или 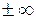 ). Неопределенности
). Неопределенности 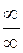 или
или  это
это 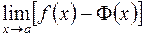 , когда обе функции
, когда обе функции 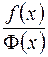 не будет неопределенностью. Например, если
не будет неопределенностью. Например, если 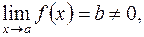

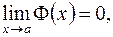
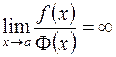 .
. . Аналогичный смысл имеют и следующие равенства:
. Аналогичный смысл имеют и следующие равенства: 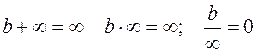 .
.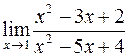 .
.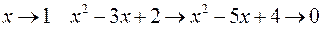 . Имеем неопределенность
. Имеем неопределенность  .
. .
.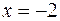 не принадлежит области определения данной функции, причем
не принадлежит области определения данной функции, причем 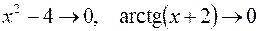 при
при 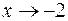 . Имеем неопределенность
. Имеем неопределенность 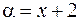 . При
. При 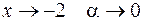 . Тогда
. Тогда 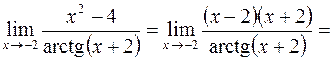
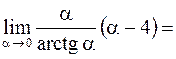
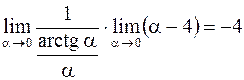 . Здесь мы воспользовались тем, что
. Здесь мы воспользовались тем, что 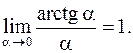
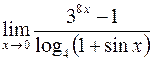 .
.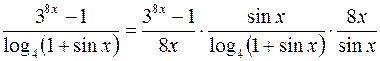 и вычислим предел каждого сомножителя отдельно (см.п.2)
и вычислим предел каждого сомножителя отдельно (см.п.2) 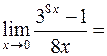
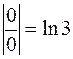 .
.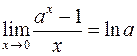 );
);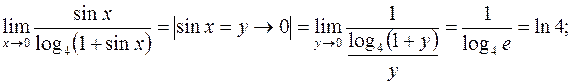
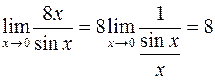 .
.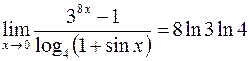 .
.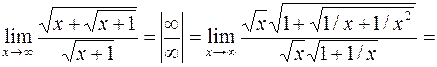
 .
.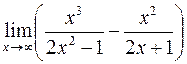 .
.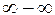 , т.к.
, т.к.
 ,
,  при
при 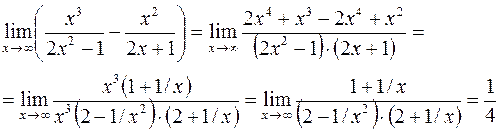 .
.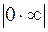 . Неопределенность этого вида возникает при вычислении
. Неопределенность этого вида возникает при вычислении 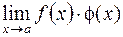 , когда
, когда  ,
, 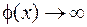 при
при 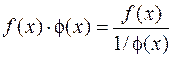 или
или  .
.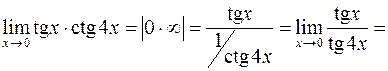
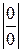 =
=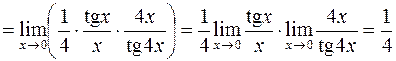 .
. .
. . При
. При 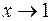 имеем
имеем 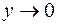 . Поэтому
. Поэтому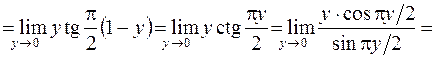

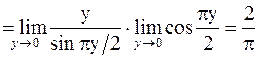 .
.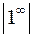 . Говорят, что
. Говорят, что  есть неопределенность
есть неопределенность 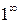 . Если
. Если 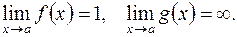 Данная неопределенность иногда сводится ко второму замечательному пределу. Для этогооснование
Данная неопределенность иногда сводится ко второму замечательному пределу. Для этогооснование 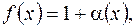 где
где 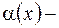 б.м. при
б.м. при 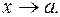 В других случаях неопределенность этого вида может быть сведена к неопределенности
В других случаях неопределенность этого вида может быть сведена к неопределенности 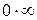 путем преобразования:
путем преобразования: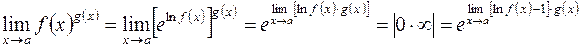 (2)
(2)
 при
при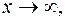 следовательно, имеем неопределенность
следовательно, имеем неопределенность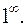 Сведем ее ко второму замечательному пределу. Для этого заметим, что
Сведем ее ко второму замечательному пределу. Для этого заметим, что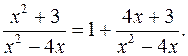
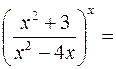
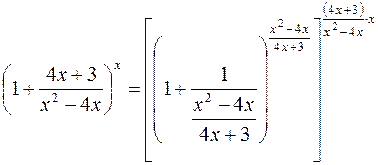
 видим, что при
видим, что при  тогда
тогда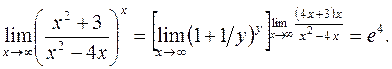
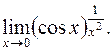
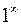 .
.
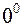 . Данная неопределенность связана с пределами вида
. Данная неопределенность связана с пределами вида 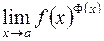 , когда функции
, когда функции 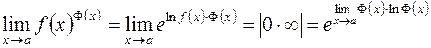 .
.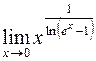 .
.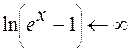 при
при  , тогда
, тогда  . Таким образом, имеем неопределенность
. Таким образом, имеем неопределенность 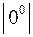 . Раскроем вышеуказанным способом:
. Раскроем вышеуказанным способом:
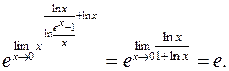
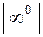 .
. , тогда
, тогда 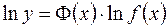 . Предел
. Предел  представляет собой неопределенность уже изученного вида
представляет собой неопределенность уже изученного вида 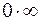 . Допустим, что одним из указанных выше приемов нам удалось ее раскрыть и мы получили конечный предел
. Допустим, что одним из указанных выше приемов нам удалось ее раскрыть и мы получили конечный предел 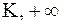 или
или 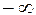 . Тогда
. Тогда  будет, соответственно, равен
будет, соответственно, равен 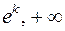 или
или 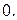 Точно также можно поступить и в случае неопределенностей
Точно также можно поступить и в случае неопределенностей 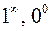 .
.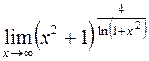 .
.