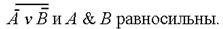|
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Решение логических задач. Примеры решения задач ⇐ ПредыдущаяСтр 7 из 7
Примеры решения задач Пример 1 Какой логической операции соответствует таблица истинности?
F=A → B Таблица истинности соответствует логической функции «импликация». Пример 2 Найти значение логического выражения при А=0 (false), В=1 (True), С=0 (False). Решение: подставим значения переменных в выражение и вычислим его согласно приоритету выполнения операций:
Ответ: данное логическое выражение имеет значение True. Пример 3 Найти значение логического выражения: (А<В) v (В>2) v (А ≠ 5) при А=5, В=-4. Решение: Подставим значения переменных в выражение и вычислим его согласно приоритету выполнения операций: (5<-4) v (-4>2) v (5 ≠ 5)=0 v 0 v 0=0. Пример 4 Упростить логическое выражение: (А & В) v (А & Решение: Воспользуемся законом диструбтивности и вынесем за скобки А: (А & В) v (А & По закону исключённого третьего В v А & (В v Таким образом (А & В) v (А & Составим таблицу истинности для выражения (А & В) v (А &
Пример 5 По заданной логической схеме составить логическое выражение и заполнить для него таблицу истинности.
Решение: Используя обозначения логических элементов, составим логическое выражение Заполним для F таблицу истинности
Пример 6 Какое из приведённых имён удовлетворяет логическому условию: (первая буква согласная → вторая буква согласная) Λ (предпоследняя буква гласная → последняя буква гласная)? 1) КРИСТИНА 2) МАКСИМ 3) СТЕПАН 4) МАРИЯ Решение: Имя должно удовлетворять условию, значит, F=1. Заменим выражения на логические переменные: первая буква согласная – А вторая буква согласная – В предпоследняя буква гласная – С последняя буква гласная – D (A→B)Λ(C→D) = 1. Расставляем приоритеты логических операций. Сначала должна выполняться конъюнкция. Чтобы выражение было равно 1, необходимо, чтобы (A→B) = 1 и (C→D) = 1. Теперь рассмотрим импликации. В каждой из них есть по 3 возможных варианта, когда импликация равна 1. A→B = 1.
C→D=1.
Теперь будем проверять каждое имя. КРИСТИНА: А=1, В=1, С=0, D=1 .A→B=1.C→D=1. Следовательно, это имя подходит. МАКСИМ: А=1, В=0, С=1, D=0. A→B=0. C→D=0. Следовательно, это имя не подходит. СТЕПАН: А=1 ,В=1, С=1, D=0 .A→B=1 .C→D=0. Следовательно, это имя не подходит. МАРИЯ: А=1,В=0,С=1,D=1.A→B=0.C→D=1. Следовательно, это имя не подходит. Пример 7 Дан фрагмент таблицы истинности выражения F:
Какое выражение соответствует F? 1) X Λ Y Λ Z 2) X V Y V Z 3) X V Y V Z 4) XΛYΛZ Решение: Будем решать подстановкой предлагаемых вариантов. 1) F=X Λ Y Λ Z = 1 только в случае, когда X, Y, Z = 1. Проверяем по таблице. Этому условию не удовлетворяют вторая и третья строки таблицы. 2) F=XVY V Z. Подставляем значения из таблицы: для первой строки F=0 V 0 V 1=1 в случае, когда хотя бы одно из значений X, Y или Z =1 для второй строки F = 0 V 0 V 0=0. Следовательно, не подходит. 3) F=X V Y V Z=1 Проверяем по таблице. Подходит для всех трёх строк таблицы. 4) F=XΛYΛZ. Подставляем значения из таблицы: F = 0 Λ 0 Λ 0=0. Следовательно, не подходит. Ответ: выражение 3) F=X V Y V Z=1 Пример 8 Укажите, какое логическое выражение равносильно выражению: A V (B ΛC): 1) A V B V C 2) A V (B Λ C) 3) A V B V C 4) A V B V C Решение: выносим за скобки операцию отрицания AV(BΛC)=AV(BΛC) двойное отрицание логического выражения AV(BΛC) даёт выражение Ответ: AV(BΛC) = A V (B Λ C). Тесты 1. Наука, изучающая законы и формы мышления, называется: а) алгеброй; б) геометрией; в) философией; г) логикой. 2. Повествовательное предложение, в котором что-то утверждается или отрицается, называется: а) выражением; б) вопросом; в) высказыванием; г) умозаключением. 3. Какое из следующих высказываний является истинным: а) город Париж – столица Англии; б) 3+5=2+4; в) II + VI = VIII; г) томатный сок вреден. 4. Объединение двух высказываний в одно с помощью союза «и» называется: а) инверсией; б) конъюнкцией; в) дизъюнкцией; г) импликацией. 5. Логической операцией не является: а) логическое деление; б) логическое сложение; в) логическое умножение; г) логическое отрицание. 6. Логическая функция – это: а) простое высказывание; б) составное высказывание; в) вопросительное предложение; г) логическая операция. 7. Объединение двух высказываний в одно с помощью оборота «если…, то…» называется: а) инверсией; б) конъюнкцией; в) дизъюнкцией; г) импликацией. 8. Таблица, содержащая все возможные значения логического выражения, называется: а) таблицей ложности; б) таблицей истинности; в) таблицей значений; г) таблицей ответов. Задания Задание 1. Какой логической операции соответствует таблица истинности?
Задание 2. Какой логической операции соответствует таблица истинности?
Задание 3. Найти значения приведённых ниже логических выражений:
(X > Y) V (Z <4 ) при X = 5, Y = 7, Z = 0.
(a < z) V (z > -10) & (a ≠ 5) при a = 8, z = -6.
Задание 4. Задано логическое выражение Задание 5. Упростить логическое выражение Задание 6. Доказать данное равенство с помощью таблицы истинности.
Задание 7. По заданным логическим выражениям составить логические схемы и заполнить таблицы истинности: · Записать составное высказывание «(2 • 2 = 4 и 3 • 3 = 9) или (2 • 2 ≠ 4 и 3 • 3 ≠ 9)» в форме логического выражения. · Построить таблицу истинности. Задание 8. Доказать, используя таблицы истинности, что логические выражения
Задание 9. Вадим, Сергей и Михаил изучают различные иностранные языки – китайский, японский и арабский. На вопрос: “какой язык изучает каждый из них”, – один ответил: «Вадим изучает китайский, Сергей не изучает китайский, а Михаил не изучает арабский». Потом выяснилось, что в этом ответе только одно утверждение верно, а два других ложны. Какой язык изучает каждый из молодых людей? Задание 10. Три одноклассника – Влад, Тимур и Юра встретились спустя 10 лет после окончания школы. Выяснилось, что один из них стал врачом, другой физиком, а третий юристом. Один полюбил туризм, другой бег, третий – регби. Юра сказал, что на туризм ему не хватает времени, хотя его сестра – единственный врач в семье, заядлый турист. Врач сказал, что он разделяет увлечение коллеги. Забавно, но у двоих из друзей в названиях их профессий и увлечений не встречается ни одна буква их имён. Определите, кто, чем любит заниматься в свободное время и у кого какая
Поиск по сайту: |
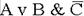 ,
, =0 v 1 &
=0 v 1 &  =0 v 1& 1=0 v 1=1 (True).
=0 v 1& 1=0 v 1=1 (True).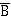 ). Правильность упрощения проверить с помощью таблиц истинности.
). Правильность упрощения проверить с помощью таблиц истинности.
 .
.
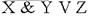
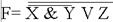
 А & В V C при А =0(False), В = 1(True), C = 0 (False).
А & В V C при А =0(False), В = 1(True), C = 0 (False). A V В при A = False, B = False.
A V В при A = False, B = False. & C при А =False, В = False, C = True.
& C при А =False, В = False, C = True.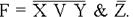 Составить логическую схему для данного выражения и заполнить таблицу истинности.
Составить логическую схему для данного выражения и заполнить таблицу истинности. V
V  . Правильность упрощения проверить с помощью таблицы истинности.
. Правильность упрощения проверить с помощью таблицы истинности.
 X ↔ Y = (X & Y) V (X & Y)
X ↔ Y = (X & Y) V (X & Y)