 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Закон исключённого третьего
Высказывание может быть либо истинным, либо ложным – третьего не дано. Это означает, что результат логического сложения высказывания и его отрицания всегда принимает значение «истина»: А v Ā=1. Закон двойного отрицания Если дважды отрицать некоторое высказывание, то в результате мы получим исходное высказывание:
Законы де Моргана (общей инверсии)
Важное значение для выполнения преобразований логических выражений имеют законы алгебраических преобразований. Многие из них имеют аналоги в обычной алгебре. Закон коммутативности (переместительный) В обычной алгебре слагаемые и множители можно менять местами. В алгебре высказываний можно менять местами логические переменные при операциях логического умножения и логического сложения: Логическое умножение А & В = В & А. Логическое сложениеAvВ= AvВ. Закон ассоциативности (сочетательный) Если в логическом выражении используются только операция логического умножения или только операция логического сложения, то можно пренебрегать скобками или произвольно их расставлять: Логическое умножение Логическое сложение (А & B) & С =A & (B & С). (Av В)v С = A v (B v С). Закон дистрибутивности (распределительный) В отличие от обычной алгебры, где за скобки можно выносить только общие множители, в алгебре высказываний можно выносить за скобки как общие множители, так и общие слагаемые:
Рассмотрим в качестве примера применения законов логики преобразование логического выражения. Пусть нам необходимо упростить логическое выражение (А & В) v (А & Воспользуемся законом дистрибутивности и вынесем за скобки А: (А & В) v (А & По закону исключённого третьего В v
Логические элементы Работа современных вычислительных машин сводится к обработке последовательностей нулей и единиц, которыми закодирована различная информация (числовая, графическая звуковая), и пересылки этой информации. Такую обработку производит арифметико-логическое устройство, являющееся частью процессора. Состоит оно из логических элементов. Логическими элементами компьютеров являются электронные схемы И, ИЛИ, НЕ, И—НЕ, ИЛИ—НЕ и другие (называемые также вентилями), а также триггер. С помощью этих схем можно реализовать любую логическую функцию, описывающую работу устройств компьютера. Обычно у вентилей бывает от двух до восьми входов и один или два выхода. Чтобы представить два логических состояния — “1” и “0” в вентилях, соответствующие им входные и выходные сигналы имеют один из двух установленных уровней напряжения. Например, +5 вольт и 0 вольт. Высокий уровень обычно соответствует значению “истина” (“1”), а низкий — значению “ложь” (“0”). Каждый логический элемент имеет своё условное обозначение, которое выражает его логическую функцию, но не указывает на то, какая именно электронная схема в нём реализована. Это упрощает запись и понимание сложных логических схем. Работу логических элементов описывают с помощью таблиц истинности.
Поиск по сайту: |
 =А.
=А. = Ā &
= Ā & 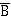 ;
; = Ā
= Ā 

