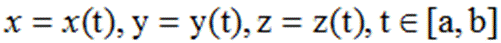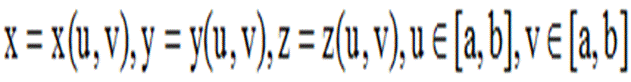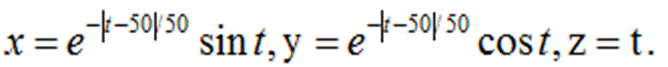Plot(x,y,'color_style_marker')

22 -18 12

-6 10 -6

16 -18 20

Баған мен жол сәйкес келсе матрица көбейтіледі. Егер өлшемдері сәйкес келмесе қосу орындалмайды.

>> a=[1 2 3;1 2 3]

a =

1 2 3

1 2 3

A 3*2

17. Сызықтық теңдеулер жүйесін шешіңіз:

>> A=[3 3 4 5;2 6 4 6;3 4 5 5;1 9 3 6];

>> b=[1;4;0;3];

>> x=A\b

x =

-4.5000

-1.6250

0.6250

3.3750

18. Сызықтық теңдеулер жүйесін шешіңіз

>> A=[2 1 5 2;5 2 2 6;2 2 1 2;1 3 3 1];

>> b=[1;3;;0;2];

>> x=A\b

x =

-5.4762

0.5238

0.3810

4.7619

19. Матрицалардың қосындысы мен көбейтіндісін есептеңіз

>> A=[5 8 10;4 -5 5;-9 1 3];

>> B=[1 4 8;-8 5 9;-8 5 6];

>> c=A+B

c =

6 12 18

-4 0 14

-17 6 9 ----БҰЛ ҚОСУ

>> A=[5 8 10;4 -5 5;-9 1 3];

>> B=[1 4 8;-8 5 9;-8 5 6];

>> c=A*B

c =

-139 110 172

4 16 17

-41 -16 -45 ---- БҰЛ КӨБЕЙТУ

20. Сызықтық теңдеулер жүйесін шешіңіз:

>> A=[3 6 5 7;4 6 3 5;2 3 2 6;2 4 3 6];

>> b=[3;0;4;3];

>> c=A\b

c =

1.0000

-2.0000

1.0000

1.0000

21. Мына формулармен анықталатын, үшөлшемді сызықтарды құру есебін жазыңыз

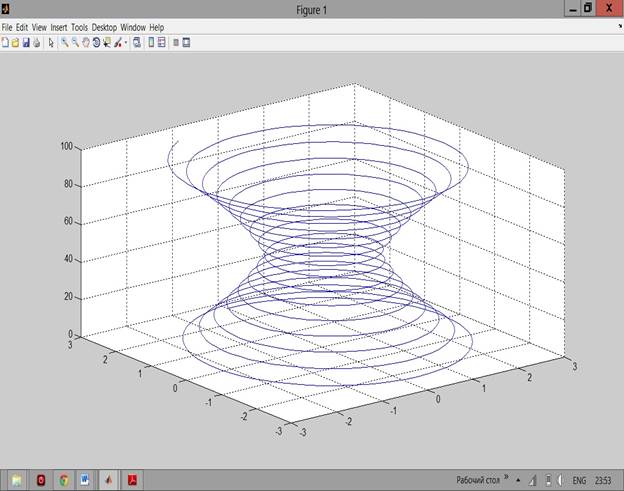
>> t=[0:0.1:100];

>> x=exp(abs(t-50)/50).*sin(t);

>> y=exp(abs(t-50)/50).*cos(t);

>> z=t;

>> plot3(x,y,z)

>> grid on

22. Мына формулармен анықталатын, үшөлшемді беттерді құру есебін жазыңыз

T=[1:10];

X=sin(t);

Y=cos(t);

Z=t;

[x,y]=meshgrid[-2:0.01:2];

Plot(x,y,z)

23. Мына координаталарымен анықталатын, нүкте қозғалысын жазыңыз

t=[0:0.001:10];

>> x=[sin(t)./(t+1);

y=cos(t)./(t+1);

??? y=cos(t)./(t+1);

Comet(x,y)

24. Мынандай координатамен қозғалатын нүктенің бағытын тұрғызыңыз

>> t=[0:0.1:100];

>> x=exp(abs(t-50)/50).*sin(t);

>> y=exp(abs(t-50)/50).*cos(t);

>> z=t;

>> comet3(x,y,z)

41. Арифметикалық амалдарды Матлаб жүйесінде шешудің негізгі жолы. Қандай терезелер қолданылады. Мысал келтіріңіз.

MatLab – техникалық есептеулер үшін қажетті тіл. Ол есептер мен оның шешімдерін математикаға жақын түрде өрнектеу үшін керекті тиімді ортада бағдарламалау, визуализациялау және есептеулерден тұрады. Жұмыс ортасы келесі негізгі элементтерден тұрады:

- меню;

- тізімі, батырмалары бар саймандар тақтасы;

Workspace, Current Directory командалары(айнымалыларды қарау жәнеағымдағы каталогты орнату үшін қажет) бар терезе;

Командаларды енгізуге және нәтижені шығаруға арналған Command Window

терезесі;

Бұрын енгізілген командаларды қайта орындау және қарау үшін керекті Command History терезесі;

Айнымалылар –әдетте мағынасы әр түрлі кейбір мәліметтерді сақтай алатын атыбар объектілер.Осы мәліметтерге байланысты айнымалылар сандық және символдық, векторлық немесе матрицалық болып бөлінеді. Айнымалылар математика мен бағдарламалауда кең тараған объект болып табылады. MatLab бағдарламалау тілінде шамасы анықталған айнымалыларды ғана беруге болады. Ол үшін меншіктеу операциясы қолданылады, ол = таңбасымен енгізіледі.

Айнымалы аты = шама

Айнымалы типтері алдын ала декларацияланады. Олардың шамасы айнымалыға меншіктеледі. Егер осы шама вектор немесе матрица болса, онда айнымалы вектор немесе матрица болады. Тек бір мәні бар айнымалы 1х1 өлшемді матрица ретінде қарастырылады.

Айнымалы атының (оның идентификаторы)қанша символдан тұратыны маңыздыемес, алайда бастапқы 31 символы ғана сақталады және идентификацияланады. Кез – келген айнымалының аты басқа айнымалының, функцияның, процедуралардың атымен сәйкес келмеуі керек, яғни ерекше болуы керек. Аты әріптен басталуы керек, әріптен, саннан және асты сызылған символдан тұруы мүмкін. Айнымалы атына бос орын мен арнайы таңба қосылмайды, мысалы +, -, *, /және т. б., себебі осындай жағдайда дұрыс интерпретацияланбайды.

Мағынасы бар аттарды қолдану керек, мысалы бірінші объектінің жылдамдығын білдіретін айнымалы үшін speed_1

Айнымалылар қарапайым және индекстелген болуы мүмкін, яғни вектор немесе матрица элементтері қолданылуы мүмкін. Символдық шамалар да қолданылуы мүмкін, онымен қоса символдық шамалар апострофпен бекітіледі, мысалы s='Demo'. Айнымалы аттарын тек латын әріптерімен, санымен және әр түрлі символдарымен жазылу керек (оператор символы қолданылмайды).

Кескіндеме редакторы – бұл MatLab жүйесінің арнайы жаңа графикалық әдісі. Ол M_файлдармен құрылып қойылған немесе графиктің командалық жолындағы командалармен құрылған графиктерді редакторлау үшін, сонымен қатар тұтынушы берілген тип бойынша графикті құру үшін арналған. Графикті редакторлауда график терезесінен, осы терезенің менюінен және MatLab жүйесінің терезесіндегі Graphics менюінен шығаруға болады. Егер графикті тұрғызуға керекті массив енгізілген болса және жұмыс аумағының браузері ашық болатын болса, онда Graphics менюінің график тұрғызу мүмкіншілігі үшін артықшылығы командалар жиынтығымен көбейеді.

MatLab жүйесінің керемет қырларының бірі есептеуді визуализациялау. Бір айнымалысы бар функциялар графиктерін сызу мысалдарын көрсетейік.

Plot функциясы көмегімен график сызып көрейік.Ол кіріс аргументтерінебайланысты әртүрлі формада болады. Егер у-вектор болса, онда plot(y) у элементтерінің индексіне байланысты элементтердің үзік сызықты графигін шығарып береді. Ал, егер plot(х,y) функциясы бірдей өлшемді екі векторлық аргументтерден тұрса,онда х мәндерінетәуелді у-тің графигі шығады.

Мысалы, y = sin(t) функциясының [0;2] аралығындағы мәнін график түрінде шығару үшін келесі команданы енгізсек жеткілікті

» t = 0:pi/100:2*pi;

» y = sin(t);

» plot(t,y)

44. Екі айнмалыдан түратын функцияның f(x,y), f(t,x), f(y,z) Matlab жүйесінде шешудың мәні, анализ жасаңыз.

Кескіндеме редакторы – бұл MatLab жүйесінің арнайы жаңа графикалық әдісі. Ол M_файлдармен құрылып қойылған немесе графиктің командалық жолындағы командалармен құрылған графиктерді редакторлау үшін, сонымен қатар тұтынушы берілген тип бойынша графикті құру үшін арналған. Графикті редакторлауда график терезесінен, осы терезенің менюінен және MatLab жүйесінің терезесіндегі Graphics менюінен шығаруға болады. Егер графикті тұрғызуға керекті массив енгізілген болса және жұмыс аумағының браузері ашық болатын болса, онда Graphics менюінің график тұрғызу мүмкіншілігі үшін артықшылығы командалар жиынтығымен көбейеді.

MatLab жүйесінің керемет қырларының бірі есептеуді визуализациялау. Екі айнымалысы бар функциялар графиктерін сызу мысалдарын көрсетейік.

Plot функциясы көмегімен график сызып көрейік.Ол кіріс аргументтерінебайланысты әртүрлі формада болады. Егер у-вектор болса, онда plot(y) у элементтерінің индексіне байланысты элементтердің үзік сызықты графигін шығарып береді. Ал, егер plot(х,y) функциясы бірдей өлшемді екі векторлық аргументтерден тұрса,онда х мәндерінетәуелді у-тің графигі шығады.

Мысалы, y = sin(t) функциясының [0;2] аралығындағы мәнін график түрінде шығару үшін келесі команданы енгізсек жеткілікті

» t = 0:pi/100:2*pi;

» y = sin(t);

» plot(t,y)

Нәтижесі 5.1 суреттегідей болады.

Егер алдыңғы өрнекке y2 = sin(t-0.25) және y3 = sin(t-0.5) функцияларын қоссақ, онда 3 түрлі түстегі қисықты (5.2 сурет) шығарып береді:

>> t = 0:pi/100:2*pi;

>> y1 = sin(t);

>> y2 = sin(t-0,25);

>> y3 = sin(t-0,5);

>> plot(t,y1,t,у2,t,у3)

Сондай-ақ сызықтың түсін, стилін және маркерін көрсетуге болады, мысалы:

plot(x,y,'color_style_marker')

color_style_marker 1, 2 немесе 3-символдық қатар (ол ' ' тырнақшасына алынып жазылады):

- түс қатарлары - 'c', 'm', 'y', 'r', 'g', 'b', 'w', и 'k'. Ол сианға, фуксинға, сарыға,

қызылға, жасылға, көкке, аққа және қараға (cyan, magenta, yellow, red, green, blue, white, and black.) сәйкес келеді.

- сызықтың стилінің қатары - '-' тұтас сызық, '- -' үзік сызық, ':' қос нүктелік, '-.' нүктелік, және 'none' бос қатар сызығы.

- маркер қатары - '+', 'o', '*' және 'x'.

Мысалы, plot(x,y,'y:+') өрнегі сары, қос нүктесі бар, +-тен құралған сызықты шығарады. Бірақ ол тек бір функциядан тұратын графикке арналған, егер екі немесе одан да көп функция болса, онда тек екі орынды символдық қатарды көрсету керек, әйтпесе қате шығады.

Келесі мысалда (5.3 суретте) графикке абцисса мен ордината остерін, сызық түрлерін көрсетейік және торлайық.

>> t=0:pi/50:1.5*pi;

>> y1=t.*cos(t);

>> y2=t.*cos(2*t);

>> plot(t,y1,'g^',t,y2,'r*');

>> xlabel('x');

>> ylabel('y');

>> legend('y1','y2')

>> grid on

>> title('Example 2');

Екі өлшемді (2D) графиктерге қарағанда үш өлшемді графиктерді форматтаудың қосымша мүмкіндіктері болады.

Екі өлшемді графиктерді тұрғызудағы қолданылатын функциялар

45. Үш айнмалыдан түратын функцияның f(x,y), f(t,x), f(y,z) Matlab жүйесінде шешудың мәні, анализ жасаңыз.

MatLab-тың кеңістіктегі графиктік мүмкіндіктері үлкен. Онда үш өлшемді графиктер сызу үшін негізінен plot3, mesh және surf функциялары қолданылады. Олардың ішінде ең қарапайымы plot3 функциясы.

MatLab-тың кеңістіктегі графиктік мүмкіндіктері үлкен. Онда үш өлшемді графиктер сызу үшін негізінен plot3, mesh және surf функциялары қолданылады. Олардың ішінде ең қарапайымы plot3 функциясы.

plot3(…) командасыplot(…)командасына ұқсайды,бірақ ол y(x)бір айнымалысыбар функцияға емес, z(x,y) екі айнымалысы бар функцияға арналған. Ол кеңістіктің (3D) аксонометриялық кескінін береді. Қарапайым жағдайда ол өлшемдері бірдей векторлардың X,Y,Z үш аргументінің функциялары болып табылады. Төртінші аргумент сызық түсін, нүктесін көрсетеді.

Айталық z=f(x,y) функциясының графигін сызу керек болсын. Ол plot3(x,y,z) функциясы арқылы орындалады. Әрине бұл функцияны қолданудан алдын x,y және z-тің мәндері анықталған болуы тиіс.

Мысалы:

» x=-1:0.1:1;

» y=-2:0.2:2;

» z=exp(-x.^2-y.^2);

» plot3(x,y, z)

» grid on

>> bar3 Үш өлшемді бағаналық диаграмма

>> bar3h Горизонтальды орналасуы бар үш өлшемді бағаналық диаграмма

>> comet3 Үш өлшемді кеңістікте нүктенің траектория бойымен қозғалысы

>> contourf Боялған облыстардағы деңгей сызықтарының графигі

>> fill3 Үш өлшемді график кеңістігінде көпбұрыштардың боялуы

>> pie3 Секторлы диаграмма

>> quiver3 Үш өлшемді кеңістікте берілген өріс бағыттарының графигі

>> slice Үштік өзгергіштердің функция қималары

>> stem3 Үш өлшемді кеңістікте дискреттік мағыналардың графигі

>> trimesh Үшбұрышты ұяшықтары бар үш өлшемді бет

>>

>> trisurf Үшбұрышты ұяшықтары бар үш өлшемді торлы бет

>> waterfall Тор қабырғалары болмайтын үш өлшемді бет

>>

46. Бірнеше айнмалыдан түратын теңдеулерден алынған графиктеріне өзгертулер жасау. Xlabel, Ylabel, Zlabel, Title. Line color.

Сондай-ақ сызықтың түсін, стилін және маркерін көрсетуге болады, мысалы:

Поиск по сайту: