\  (2).
Различают глобальную и локальную интерполяцию. Простейшим видом глобальной интерполяции является параболическая интерполяция, когда, используя описанные выше условия (2), для отыскания неизвестных n + 1 коэффициентов а0, а1, . . ., аn выражения (1) получают систему из n + 1 уравнений (2).
Различают глобальную и локальную интерполяцию. Простейшим видом глобальной интерполяции является параболическая интерполяция, когда, используя описанные выше условия (2), для отыскания неизвестных n + 1 коэффициентов а0, а1, . . ., аn выражения (1) получают систему из n + 1 уравнений
 (3).
Для интерполяции используют интерполяционную формулу Лагранжа (3).
Для интерполяции используют интерполяционную формулу Лагранжа  (4).
Для построения интерполяционной формулы Лагранжа в MathCAD используют функцию if, записанной в виде if(cond, tval, fval) -возвращает значение tval, если cond отличен от 0 (истина); возвращает значение fval, если cond равен 0 (ложь).
Интерполяция при большом числе узлов приводит к необходимости работать с многочленами высокой степени, 50-й или 100-й. Это приводит к проблемам при вычислениях. Поэтому часто используют интерполяцию кусочными многочленами (локальная интерполяция).
При локальной интерполяции между различными узлами выбираются различные многочлены невысокой степени. В MathCAD есть для этого следующие возможности: средства линейной интерполяции (функция linterp) и интерполяции сплайном (функция interp) – линейным (lspline), параболическим (pspline) и кубическим (cspline).
Интерполирование функций полиномами
Классическим методом интерполяции таблично заданных функций является интерполяция полиномами Lm(x): (4).
Для построения интерполяционной формулы Лагранжа в MathCAD используют функцию if, записанной в виде if(cond, tval, fval) -возвращает значение tval, если cond отличен от 0 (истина); возвращает значение fval, если cond равен 0 (ложь).
Интерполяция при большом числе узлов приводит к необходимости работать с многочленами высокой степени, 50-й или 100-й. Это приводит к проблемам при вычислениях. Поэтому часто используют интерполяцию кусочными многочленами (локальная интерполяция).
При локальной интерполяции между различными узлами выбираются различные многочлены невысокой степени. В MathCAD есть для этого следующие возможности: средства линейной интерполяции (функция linterp) и интерполяции сплайном (функция interp) – линейным (lspline), параболическим (pspline) и кубическим (cspline).
Интерполирование функций полиномами
Классическим методом интерполяции таблично заданных функций является интерполяция полиномами Lm(x):
 Старшая степень переменной x определяет степень полинома. Очевидно, что полином степени m полностью определяется m+1 параметром ai. Поэтому для интерполяции функции, заданной в n узлах можно использовать полином степени m = n - 1. Сравнивая выражение для Lm(x) и общее определение для математической модели, линейной по отношению к параметрам, получим, что:
Старшая степень переменной x определяет степень полинома. Очевидно, что полином степени m полностью определяется m+1 параметром ai. Поэтому для интерполяции функции, заданной в n узлах можно использовать полином степени m = n - 1. Сравнивая выражение для Lm(x) и общее определение для математической модели, линейной по отношению к параметрам, получим, что:


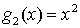 , ... , , ... ,  , ... , , ... ,  Система линейных уравнений в матричной форме примет вид
Система линейных уравнений в матричной форме примет вид
 В рамках линейной алгебры доказывается, что определитель этой матрицы (он называется определителем Вандермонда) отличен от нуля, если все xi различны, поэтому система уравнений будет иметь единственное решение.
Интерполирование полиномами помимо самостоятельной ценности в качестве инструмента решения задачи интерполирования функций, играет так же важную роль при численном решении многих других математических других задач, например, вычислении определенных интегралов, решении обыкновенных дифференциальных уравнений и многих других.
Задание по теме № 3-2. (продолжение) Решение систем линейных уравнений. Аппроксимация и интерполяция.
Ответы на задачи необходимо предоставить с точностью до шести значащих цифр.
При выполнении задания используйте методы решения систем линейных уравнений и задачи, которые к ним сводятся – интерполяция функциями и полиномами, задачи о составе смесей (в лекциях рассмотрены).
1. Зависимость теплоемкости метана от температуры описывается уравнением
В рамках линейной алгебры доказывается, что определитель этой матрицы (он называется определителем Вандермонда) отличен от нуля, если все xi различны, поэтому система уравнений будет иметь единственное решение.
Интерполирование полиномами помимо самостоятельной ценности в качестве инструмента решения задачи интерполирования функций, играет так же важную роль при численном решении многих других математических других задач, например, вычислении определенных интегралов, решении обыкновенных дифференциальных уравнений и многих других.
Задание по теме № 3-2. (продолжение) Решение систем линейных уравнений. Аппроксимация и интерполяция.
Ответы на задачи необходимо предоставить с точностью до шести значащих цифр.
При выполнении задания используйте методы решения систем линейных уравнений и задачи, которые к ним сводятся – интерполяция функциями и полиномами, задачи о составе смесей (в лекциях рассмотрены).
1. Зависимость теплоемкости метана от температуры описывается уравнением
 Найдите значение констант a, b, c, d и вычислите теплоемкость метана при 300 °С и 400 °С, если известно, что
Найдите значение констант a, b, c, d и вычислите теплоемкость метана при 300 °С и 400 °С, если известно, что
| Т, К
|
|
|
|
| | СР, Дж/(моль·К)
| 40,74
| 52,5
| 58,05
| 67,27
| 2. Даны четыре емкости с растворами кислоты различной концентрации. Если смешать растворы в определенном массовом соотношении, то получится кислота заданной процентной концентрации:
| Соотношение
| Концентрация кислоты, %
| | 1:1:1:1
|
| | 4:3:2:1
|
| | 4:1:1:4
|
| | 4:1:4:1
|
| Определите, какова концентрация кислоты в каждом из четырех сосудов.
3. Зависимость теплоемкости некоторого вещества от температуры описывается уравнением

Найдя значение констант a, b, c, d, e, вычислите теплоемкость метана при 300 K и 420 K, если известно, что
| Т, К
|
|
|
|
|
| | СР, Дж/(моль·К)
| 34,2
| 39,5
| 43,2
| 48,3
| 56,1
| 4. Состав равновесного пара над жидкой смесью бензол-толуол в зависимости от ее состава был исследован экспериментально
| % Бензола в жидкости
| % Бензола в равновесном паре
| |
|
| |
| 37.23
| |
| 71.374
| |
| 91.254
| |
|
| Аппроксимируйте экспериментальные данные полиномом максимальной степени и вычислите состав пара при содержании бензола в жидкости в 40% и 75%.
5. Экспериментально определенные температуры кипения смеси бензол-толуол в зависимости от состава приведены в таблице:
| % Бензола в жидкости
| t, °С
| |
| 110.05
| |
|
| |
| 92.3
| |
| 87.29
| |
| 84.99
| |
| 80.13
| Опишите экспериментальные данные полиномом максимальной степени и вычислите температуру кипения при содержании бензола в жидкости в 40% и 60%.
6. Экспериментально определенные температуры кипения смеси бензол-толуол в зависимости от состава приведены в таблице:
| % Бензола в жидкости
| t, °С
| | 0.001
| 110.05
| |
| 105.31
| |
| 101.46
| |
| 95.05
| |
| 89.74
| Аппроксимируйте экспериментальные данные следующей функцией

(ω –процентная доля бензола в жидкости) и вычислите температуру кипения при содержании бензола в жидкости в 15% и 45%.
7. Зависимость теплоемкости некоторого вещества от температуры описывается уравнением

Найдя значение констант a, b, c, d, e, вычислите теплоемкость метана при 300оС и 400оС, если известно, что
| Т, К
|
|
|
|
|
| | СР, Дж/(моль·К)
| 34,2
| 39,5
| 43,2
| 48,3
| 56,1
| 8. Экспериментальная зависимость теплоемкости некоторого вещества от температуры приведена в таблице
| Т, К
|
|
|
|
|
|
| | СР, Дж/(моль·К)
| 34,2
| 39,5
| 43,2
| 48,3
| 56,1
| 59,1
| Аппроксимируйте зависимость полиномом наибольшей степени и найдите теплоемкость при температурах 300 и 520 К.
9. Рассчитайте коэффициенты полинома четвертой степени, проходящего через следующие точки: (0,1), (2,2), (4,3), (5, -1), (6.-3). Постройте график данной зависимости на отрезке от 0 до 6. Найдите значение полинома при x=3.
| ещество
| Пик с массой
| |
|
|
|
|
|
|
|
|
|
|
|
| | СH4
|
|
|
|
|
|
|
|
|
|
|
|
| | Этан
|
|
|
|
|
|
|
|
|
|
|
|
| | С2H4
|
|
|
|
|
|
|
|
|
|
|
|
| | C2H2
|
|
|
|
|
|
|
|
|
|
|
|
| Задачи для самостоятельного решения по теме 3-2
"Решение систем нелинейных уравнений"
1. Найдите решение системы уравнений в окрестности точки x0=y0=z0=0.5 с точностью до пяти значащих цифр:
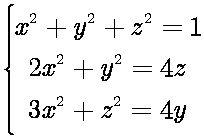
2. Найдите решение системы уравнений с точностью до пяти значащих цифр:

3. Найдите решение системы уравнений в окрестности точки x0=y0=z0=1 с точностью до пяти значащих цифр:

4. Уравнение Ван-дер-Ваальса имеет вид

Определите константы Ван-дер-Ваальса (a и b) для этана, исходя из определенных экспериментально значений молярных объемов при двух значениях давления. Если входящие в уравнение величины имеют размерность литр, атмосфера, моль и градус Кельвина, то универсальная газовая постоянная R будет равна 0,08206 л∙атм/(моль∙К).
Экспериментальные данные для 1 моль (n = 1) этана при 400К:
р = 3,2486 атм при V = 10 л р = 29,577 атм при V = 1 л.
5. Найдите решение системы уравнений:

6. Найдите минимум функции и ее минимальное значение в окрестности точки (x0,y0,z0)= (1,1,1) с точностью до 4-х значащих цифр:

7. Найдите решение системы уравнений с точностью до пяти значащих цифр:

8. Найдите решение системы уравнений с точностью до пяти значащих цифр:

9. Найдите решение системы уравнений с точностью до пяти значащих цифр:

10. Уравнение состояния реального газа Бертло для 1 моль газа имеет вид

Определите константы уравнения (a и b), исходя из определенных экспериментально значений молярных объемов при двух значениях давления.
Если входящие в уравнение величины имеют размерность литр, атмосфера, моль и градус Кельвина, то универсальная газовая постоянная R будет равна 0,08206 л∙атм/(моль∙К).
Экспериментальные данные при 400К: р = 3,2486 атм при V = 10 л
р = 29,577 атм при V = 1 л.
11.Найдите решение системы уравнений с точностью до шести значащих цифр:

12.Найдите минимум функции и ее минимальное значение с точностью до 6-ти значащих цифр:

13. Найдите решение системы уравнений с точностью до шести значащих цифр:

14. Найдите максимум функции и ее максиимальное значение с точностью до 6-ти значащих цифр:

15. Найдите минимум функции и ее минимальное значение с точностью до 6-ти значащих цифр:
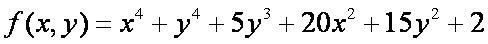
16. Найдите решение системы уравнений с точностью до шести значащих цифр:

17. Найдите решение системы уравнений с точностью до шести значащих цифр:

18.Найдите решение системы уравнений с точностью до шести значащих цифр:

19.Найдите решение системы уравнений с точностью до шести значащих цифр:

20. Найдите минимум функции и ее минимальное значение с точностью до 6-ти значащих цифр:
  , , 
21.Найдите минимум функции и ее минимальное значение с точностью до 6-ти значащих цифр:
  , , 
|

 (1),
(1),
 (2).
Различают глобальную и локальную интерполяцию. Простейшим видом глобальной интерполяции является параболическая интерполяция, когда, используя описанные выше условия (2), для отыскания неизвестных n + 1 коэффициентов а0, а1, . . ., аn выражения (1) получают систему из n + 1 уравнений
(2).
Различают глобальную и локальную интерполяцию. Простейшим видом глобальной интерполяции является параболическая интерполяция, когда, используя описанные выше условия (2), для отыскания неизвестных n + 1 коэффициентов а0, а1, . . ., аn выражения (1) получают систему из n + 1 уравнений
 (3).
Для интерполяции используют интерполяционную формулу Лагранжа
(3).
Для интерполяции используют интерполяционную формулу Лагранжа  (4).
Для построения интерполяционной формулы Лагранжа в MathCAD используют функцию if, записанной в виде if(cond, tval, fval) -возвращает значение tval, если cond отличен от 0 (истина); возвращает значение fval, если cond равен 0 (ложь).
Интерполяция при большом числе узлов приводит к необходимости работать с многочленами высокой степени, 50-й или 100-й. Это приводит к проблемам при вычислениях. Поэтому часто используют интерполяцию кусочными многочленами (локальная интерполяция).
При локальной интерполяции между различными узлами выбираются различные многочлены невысокой степени. В MathCAD есть для этого следующие возможности: средства линейной интерполяции (функция linterp) и интерполяции сплайном (функция interp) – линейным (lspline), параболическим (pspline) и кубическим (cspline).
Интерполирование функций полиномами
Классическим методом интерполяции таблично заданных функций является интерполяция полиномами Lm(x):
(4).
Для построения интерполяционной формулы Лагранжа в MathCAD используют функцию if, записанной в виде if(cond, tval, fval) -возвращает значение tval, если cond отличен от 0 (истина); возвращает значение fval, если cond равен 0 (ложь).
Интерполяция при большом числе узлов приводит к необходимости работать с многочленами высокой степени, 50-й или 100-й. Это приводит к проблемам при вычислениях. Поэтому часто используют интерполяцию кусочными многочленами (локальная интерполяция).
При локальной интерполяции между различными узлами выбираются различные многочлены невысокой степени. В MathCAD есть для этого следующие возможности: средства линейной интерполяции (функция linterp) и интерполяции сплайном (функция interp) – линейным (lspline), параболическим (pspline) и кубическим (cspline).
Интерполирование функций полиномами
Классическим методом интерполяции таблично заданных функций является интерполяция полиномами Lm(x):
 Старшая степень переменной x определяет степень полинома. Очевидно, что полином степени m полностью определяется m+1 параметром ai. Поэтому для интерполяции функции, заданной в n узлах можно использовать полином степени m = n - 1. Сравнивая выражение для Lm(x) и общее определение для математической модели, линейной по отношению к параметрам, получим, что:
Старшая степень переменной x определяет степень полинома. Очевидно, что полином степени m полностью определяется m+1 параметром ai. Поэтому для интерполяции функции, заданной в n узлах можно использовать полином степени m = n - 1. Сравнивая выражение для Lm(x) и общее определение для математической модели, линейной по отношению к параметрам, получим, что:


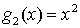 , ... ,
, ... ,  , ... ,
, ... ,  Система линейных уравнений в матричной форме примет вид
Система линейных уравнений в матричной форме примет вид
 В рамках линейной алгебры доказывается, что определитель этой матрицы (он называется определителем Вандермонда) отличен от нуля, если все xi различны, поэтому система уравнений будет иметь единственное решение.
Интерполирование полиномами помимо самостоятельной ценности в качестве инструмента решения задачи интерполирования функций, играет так же важную роль при численном решении многих других математических других задач, например, вычислении определенных интегралов, решении обыкновенных дифференциальных уравнений и многих других.
Задание по теме № 3-2. (продолжение) Решение систем линейных уравнений. Аппроксимация и интерполяция.
Ответы на задачи необходимо предоставить с точностью до шести значащих цифр.
При выполнении задания используйте методы решения систем линейных уравнений и задачи, которые к ним сводятся – интерполяция функциями и полиномами, задачи о составе смесей (в лекциях рассмотрены).
1. Зависимость теплоемкости метана от температуры описывается уравнением
В рамках линейной алгебры доказывается, что определитель этой матрицы (он называется определителем Вандермонда) отличен от нуля, если все xi различны, поэтому система уравнений будет иметь единственное решение.
Интерполирование полиномами помимо самостоятельной ценности в качестве инструмента решения задачи интерполирования функций, играет так же важную роль при численном решении многих других математических других задач, например, вычислении определенных интегралов, решении обыкновенных дифференциальных уравнений и многих других.
Задание по теме № 3-2. (продолжение) Решение систем линейных уравнений. Аппроксимация и интерполяция.
Ответы на задачи необходимо предоставить с точностью до шести значащих цифр.
При выполнении задания используйте методы решения систем линейных уравнений и задачи, которые к ним сводятся – интерполяция функциями и полиномами, задачи о составе смесей (в лекциях рассмотрены).
1. Зависимость теплоемкости метана от температуры описывается уравнением
 Найдите значение констант a, b, c, d и вычислите теплоемкость метана при 300 °С и 400 °С, если известно, что
Найдите значение констант a, b, c, d и вычислите теплоемкость метана при 300 °С и 400 °С, если известно, что



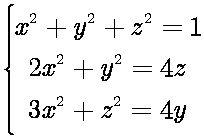













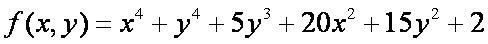





 ,
, 
