 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Обчислення координат точок в теодолітному полігоні
Лінійні та кутові вимірювання на місцевості встановлюють геометричну взаємозалежність точок земної поверхні, визначають планове положення цих точок на площині у прийнятій системі координат. Вимірювання виконуються відносно вихідних, або початкових точок, координати яких визначень заздалегідь або задані. В міру віддалення від вихідних точок нагромаджуються похибки, які неминуче супроводжують вимірювання, і, отже, точність одержаних координат точок місцевості знижується. Виникає потреба попереднього встановлення планового положення початкових точок в єдиній системі координат. Зв’язані між собою єдиною системою координат вихідні точки утворюють планові геодезичні сітки. Планове положення вихідних точок можна встановити геодезичним методом визначення координат точок прокладанням так званих теодолітних ходів. Ходом у топографії називають деяку сукупність точок, розташованих і закріплених на місцевості так, щоб забезпечити послідовне (від точки до точки) вимірювання відстоней між ними, або сторін ходу кутів, утворених цими сторонами, та перевищень між точками. Хід може бути замкнутим (полігоні) або розімкнутим. Теодолітним ходом називають хід, кути кого вимірюють теодолітом, а довжини ліній – за допомогою світла – або оптичного далекоміра, землемірної стрічки. Довжина сторони ходу не повинна перевищувати 350м і бути меншою 20м. Перед початком вимірювань точки теодолітного ходу, або точки повороту, закріплюють на місцевості. При виборі на місцеположення точок керуються зручністю подальшого використання їх та забезпеченням довгострокового збереження. Як правило, вимірюють кути між сторонами ходу (кути повороту), що лежать ліворуч за ходом і більш зручні в подальших обчисленнях. При необхідності (якщо більш за 1,50) визначають кути похилу, і вводять поправки у виміряні довжини сторін. Для визначення координат точок ходу зо допомогою формул прямої геодезичної задачі. Необхідно знати початковий дирекційний кут вихідної сторони та координати вихідних точок ходу (в існуючій або умовній системі). Ці дані можна отримати шляхом так званої прив’язки теодолітного ходу до пунктів державної геодезичної сітки, тобто включенням у нього пунктів існуючої опорної сітки. Хід не прив’язаний до пунктів геодезичної сітки, має назву вільною, таким ходом може бути замкнутий теодолітний хід. Вихідні координати однієї з точок та початковий дирекційний кут у ньому вибирають умовно. В цьому випадку вихідний дирекційний кут може дорівнювати виміряному магнітному азимуту. Кут орієнтування інших сторін ходу одержують шляхом обчислень на основі геометричної залежності між ними і кутами повороту сторін теодолітного ходу: αі = αі-1 - 1800 + βі ; де βі - лівий кут по ходу між стороною, дирекційний кут якої відомий, та стороною, для якої цей кут визначається. Читають формулу так: дирекційний кут наступної сторони дорівнює дирекційному куту попередньої сторони „мінус” 1800 + лівий по ходу горизонтальний кут. Результати обчислень координат точок теодолітного ходу за даними польових робіт через різні причини відхиляються від теоретично можливих. Різниці між ними, або нев’язки, не повинні перевищувати встановлених значень, тобто мають бути допустимими. Допустимі нев’язки ліквідують шляхом внесення в результаті обчислень – поправок. Цей процес має назву ув’язки результатів обчислення. Приклад: Нехай на місцевості проклали замкнутий теодолітний хід (рис.). Рис. Схема теодолітного полігона
α1-2
S2-3
5 β5
S4-5 β3
β4 3
Вихідні дані й польові виміри подані в табл. Подальшу роботу виконують постанно. І. Ув’язка (вирівнювання) кутових вимірів: а) Виміряні кути (β1 … - друга графа) підсумовують і одержують значення б) обчислюють теоретичну суму кутів багатокутника, за формулою , де n – число кутів по ходу; в) визначають різницю між практичною і теоретичною сумами кутів або кутову нев’язку f βпр. за формулою: f βпр.= г) визначають допустиму кутову нев’язку f βдоп. за формулою:
У нашому прикладі д) Ув’язка кутів складається з визначення поправок v1 v2… і внесення їх у польові виміри і отримання виправлених значень кутів, сума яких повинна дорівнювати теоретичній. У теодолітних ходах кутову нев’язку розподіляють з оберненим знаком порівку на всі кути, тобто поточна поправка визначається за формулою:
е) одержують виправлені значення кутів за формулою: β випрі = β вим + Контроль: сума виправлених кутів дорівнює теоретичній. ІІ Обчислення дирекційних кутів сторін полігона і перехід від них до румбів. α 2-3 = α 1-2 + 1800 – β2 α 3-4 = α 2-3 +1800 – β3… звернуть обчислення α 1-2= α 5-1+1800 – β1; В ході обчислень при необхідності додають або віднімають 3600 з тим, щоб остаточне значення дирекційного кута не було від′ємним або більшим 3600. Контроль: обчислений початковий дирекційний кут повинен дорівнювати вихідному значенню. У пр-ді 80020′. З метою спрощення подальших підрахунків від дирекційних кутів переходять до румбів сторін (за формулами). ІІІ Обчислення приросту координат. а) приріст координат знаходять за формулами пряиої геодезичної задачі:
∆XAB = Scos α; ∆YAB = Scos α; Отримані значення приросту виписують у відповідні графи. б) потім контролюють правильність підрахунків. Відомо, що алгебраїчні (з знаком) суми приросту в замкнутому полігоні повинні дорівнювати 0. Практичні значення сум відрізняються від 0, тому виникають лінійні нев’язки f∆x f∆y. Їх значення отримують підсумовуванням обчислених приростів. в) визначають загальну абсолютну лінійну нев’язку полігона.
г) відносну похибку
IV Ув’язка приросту координат. а) спочатку одержують (вносять) поправки у визначенні прирости координат:
Де Знак поправки завжди обернений до знака нев’язки. Поправки визначають до 0,001м, а потім заокруглюють до 0,01м. б) Контроль: сума поправок повинна дорівнювати нев’язці з протилежним знаком. У нашому прикладі f = +0,14м у периметрі 318,08м. На один десяток метрів припадає 0,004м. Довжина S1-2 = 60 десятків метрів отже 0,004*6=0,03м – це поправка до першого приросту. Аналогічно знаходило поправки до інших приростів повинна дорівнювати 0. V Обчислення координат точок полігона. Координати точок полігона визначають послідовно за формулою прямої геодезичної задачі: X2 = X1+∆X1-2 X3 = X2+∆X2-3 Y2 = Y1+∆Y1-2 Y3 = Y2+∆Y2-3
Контролюють обчислення визначенням координат першої точки: X1 = X5+∆X5-1 Y1 = Y5+∆Y1-2 Обчислені координати і повинні дорівнювати вихідним.
Поиск по сайту: |



 S1-2
S1-2  β2
β2 1
1 β1
β1 S5-1
S5-1

 S3-4
S3-4 практ ;
практ ; доп=
доп= 
 ′; тобто практична похибка не перевищує допустиму, отже, можна приступати до ув’язку кутів.
′; тобто практична похибка не перевищує допустиму, отже, можна приступати до ув’язку кутів. і = f βпракт : n
і = f βпракт : n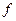 абс =
абс = 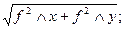



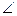 - периметр Si – прокладеня 1-2, 2-3…
- периметр Si – прокладеня 1-2, 2-3…