 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Статистична ймовірність ⇐ ПредыдущаяСтр 3 из 3
На практиці обчислити ймовірності випадкових подій можна лише для обмеженого класу задач як для дискретних, так і для неперервних просторів елементарних подій (множини Ώ). Для більшості задач, особливо економічних, обчислити ймовірності практично неможливо. У цьому разі використовується статистична ймовірність. Насамперед уводиться поняття відносної частоти випадкової події W (A). Відносною частотою випадкової події А W(A) називається відношення кількості експериментів m, при яких подія А спостерігалася, до загальної кількості n проведених експериментів:
Як і для ймовірності випадкової події, для відносної частоти виконується нерівність
Теорія ймовірностей вивчає лише такі випадкові події, в яких спостерігається стабільність відносних частот, а саме: у разі проведення k серій експериментів існує така константа Р(А), навколо якої групуватимуться відносні частоти досліджуваної випадкової події А, тобто Wі (А). І це групування буде тим ближчим до цієї константи, чим більшим буде число n експериментів. На рис. 6 показано, як Wі (А) змінюється зі збільшенням n експериментів.
Рис. 6 Імовірність випадкової події визначається так: упевнившись, що існує стабільність відносних частот випадкової події Wі (А), задаємось малим додатним числом e і проводимо серії експериментів, збільшуючи їх число n. Якщо на якомусь кроці серії експериментів виконуватиметься нерівність
1. Що називається вірогідною; неможливою подією? Навести приклади. 2. Яка подія називається випадковою? Навести приклади. 3. Яка подія називається елементарною; складеною випадковою подією? Навести приклади. 4. Що називається простором елементарних подій? Навести приклади. 5. Сумою двох випадкових подій А і В називається ... 6. Добутком двох випадкових подій А і В називається ... 7. Різницею двох випадкових подій А і В називається ... 8. Дати класичне означення ймовірності випадкової події. 9. Переставленням із n елементів називається ... 10. Розміщенням із n елементів по m називається ... 11. Комбінацією із n елементів по m називається ... 12. Що таке алгебра подій? 13. Аксіоми теорії ймовірностей. 14. Відомо, що Аі (і = 1, …, n) утворюють повну групу. Чому дорівнює 15. Відомо, що А 16. Відомо, що випадкові події А, В, С є попарно сумісними і сумісними в сукупності. Довести, що 17. Відомо, що випадкові події А, В, С, D є попарно і в сукупності сумісними. Довести, що 18. Що називається відносною частотою випадкової події? 19. Що називається геометричною ймовірністю? 20. Що таке статистична ймовірність? Приклади до теми 1. Маємо 10 лотерейних білетів. На кожний із них може випасти виграш із певною ймовірністю. Побудувати простір елементарних подій (множину Ώ) — числа білетів, на які випаде виграш, а також такі випадкові події: А — із 10 білетів виграють не більш як три; В — із 10 білетів виграють не менш як п’ять. Обчислити Р (А), Р (В), Відповідь.
2. Задано дві множини цілих чисел: Ώ1 = {1, 2, 3, 4, 5, 6, 7, 8}, Ώ2 = {1, 2, 3, 4, 5, 6}. Із кожної множини навмання беруть по одному числу. Побудувати простір елементарних подій для цього експерименту і такі випадкові події: А — сума цифр буде кратною 3; В — сума цифр буде кратною 7. Обчислити: Р (А), Р (В), Відповідь. 3. Гральний кубик підкидається один раз, а монета чотири рази. Побудувати простір таких елементарних подій — поява числа на гральному кубику і поява герба на монеті, а також випадкові події: А — на гральному кубику з’явиться число, кратне двом, і герб при цьому випаде не менш як двічі; В — на гральному кубику з’явиться число, кратне трьом, і герб при цьому випаде не більш як тричі. Обчислити: Р (А), Р (В), Відповідь. 4. В електромережу ввімкнено 15 електролампочок. Кожна з них може перегоріти із певною ймовірністю. Визначити простір елементарних подій (множину Ώ) — числа електролампочок, що не вийдуть із ладу, і такі випадкові події: А — число електролампочок, що не вийдуть із ладу, буде не більшим від чотирьох; В — від трьох до шести. Обчислити: Р (А), Р (В), Відповідь. 5. Відомо, що Р (А) = 0,9. Чому дорівнює 6. В якому разі 7. Відомо, що А Ì Ώ, В Ì Ώ. Чому дорівнює
8. В якому разі 9. Відомі значення 10. Відомі значення 11. В якому разі А \ В = А? 12. В якому разі 13. В якому разі 14. Відомо, що Аі Ì Ώ (і = 1, …, n). Чому дорівнює 15. Відомо, що Аі Ì Ώ (і = 1, n). Чому дорівнює 16. Відомі значення 17. Відомо, що А1, А4, А3, А4 є між собою несумісними і утворюють повну групу. Знайти значення Р(А1), Р(А2), Р(А3), Р(А4), якщо: Р(А1) = 0,5Р(А2) + 0,8Р(А3); Р(А2) = 0,8Р(А3) + 0,2Р(А4); Р(А3) = 0,8Р(А4). 18. Монета підкидається 20 раз. Яка ймовірність того, що при цьому герб з’явиться 7 або 17 раз? Відповідь. 19. На кожній із п’яти однакових карток написана одна із цифр 1, 2, 3, 4, 5. Навмання картки розкладають в один рядок. Обчислити ймовірність таких випадкових подій: 1) А — цифри на картках утворюють зростаючу послідовність; 2) В — спадну послідовність; 3) С — цифри 1, 2 розміщуватимуться в такій послідовності на початку рядка; 4) D — цифра 1 стоятиме на першому місці, а 5 — на останньому. Відповідь.
20. Виконується переставлення чисел 1, 2, 3 ... 10. Знайти ймовірність того, що числа 1) 1, 2; 2) 1, 2, 3, 4 будуть розміщені в наведеному порядку. Відповідь. 1) 21. Задано множину цілих чисел Ώ = {1, 2, 3, 4, 5}. Числа навмання розміщують у рядок. Яка ймовірність того, що при цьому утвориться парне п’ятицифрове число? Відповідь. 22. Маємо тринадцять однакових карток:
Відповідь. 23. Задана множина цілих чисел Ώ = {1, 2, 3, 4, 5, 6, 7, 8, 9}. Яка ймовірність того, що навмання взяті чотири числа, розміщені в рядок, утворять число 1936? Відповідь. 24. Числа 1, 2, 3, 4, 5 написані на п’яти однакових картках. Навмання послідовно по одній вибирають три картки й розкладають їх у рядок. Яка ймовірність того, що при цьому утвориться парне трицифрове число? Відповідь. 25. Дев’ять пасажирів навмання розміщуються у трьох вагонах. Обчислити ймовірність таких випадкових подій: 1) А — у кожному вагоні виявиться по три пасажири; 2) В — у першому вагоні виявиться 4 пасажири, у другому — 3 і в третьому — 2 пасажири. Відповідь.
26. В урні міститься 4 червоних, 5 синіх і 6 зелених кульок. Навмання із урни беруть три кульки. Яка ймовірність того, що вони виявляться одного кольору або всі три будуть мати різні кольори? Відповідь. 27. В урні міститься 20 кульок, пронумерованих відповідно від 1 до 20. Кульки із урни виймають по одній із поверненням. Таким способом кульки виймалися 10 раз. Яка ймовірність того, що номери кульок утворять зростаючу послідовність? Відповідь. 28. Підкидається n штук гральних кубиків. Обчислити ймовірність таких випадкових подій: 1) А — сума випадкових цифр дорівнюватиме n ; 2) В — сума цифр, що випали, дорівнюватиме n + 1. Відповідь. 1) 29. 20 студентів, серед яких 10 чоловічої статі, а решта — жіночої, навмання групуються в пари. Яка ймовірність того, що кожна пара складається зі студентів різної статі? Відповідь. 30. У бригаді робітників 5 чоловіків і 10 жінок. Яка ймовірність того, що навмання розбиваючи їх на 5 груп по три чоловіки, у кожній із них виявиться один чоловік. Відповідь. 15 робітників можна розбити на 5 трійок так: Отже, 31. Задано множину Ώ = {0 £ х £ p, 0 £ у £ 1}. Яка ймовірність того, що навмання взяті два числа x, y утворять координати точки, яка належить області А = {0 £ х £ p, 0 £ у Відповідь. Р (А) = 0,5. 32. У мішень, яка має вигляд кола, вписано квадрат. По ній здійснюється один постріл. Вважається при цьому, що влучення в коло мішені є подією вірогідною. Яка ймовірність того, що куля влучить у квадрат. Відповідь.
Поиск по сайту: |
 . (16)
. (16) .
.
 , то за ймовірність випадкової події береться одне з чисел Wі або Wі – 1. Ця ймовірність називається статистичною.
, то за ймовірність випадкової події береться одне з чисел Wі або Wі – 1. Ця ймовірність називається статистичною. ?
? В ¹ Ø. Чому дорівнює
В ¹ Ø. Чому дорівнює  ? Довести.
? Довести. ...
... ...
... .
.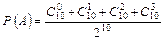 ;
; ;
; 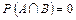 .
.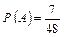 ;
; 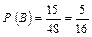 ;
;  ;
; 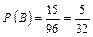 ;
; 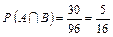 .
.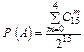 ;
; 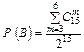 ;
;  .
.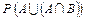 , якщо А Ì Ώ, А
, якщо А Ì Ώ, А 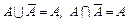 ?
?
 ?
? ,
,  ?
?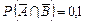 ,
, 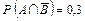 ,
,  . Знайти
. Знайти  ,
, 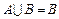 ?
? ?
? ?
? ?
? . Знайти
. Знайти  .
. ;
;  ;
; 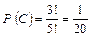 ;
; .
. ; 2)
; 2)  .
. .
. ,
, які навмання розкладають у рядок. Яка ймовірність того, що при цьому дістанемо слово «паралелепіпед».
які навмання розкладають у рядок. Яка ймовірність того, що при цьому дістанемо слово «паралелепіпед». .
. .
. .
. ;
; .
. .
. .
. ; 2)
; 2)  .
.
 .
. ; 10 жінок можна розбити на 5 груп, по дві жінки в кожній групі так:
; 10 жінок можна розбити на 5 груп, по дві жінки в кожній групі так: 
 ; 5 чоловіків можна розмістити в 5 групах 5! способами.
; 5 чоловіків можна розмістити в 5 групах 5! способами.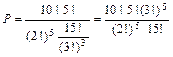 .
. }.
}. .
.