 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Класичне означення ймовірностіСтр 1 из 3Следующая ⇒
Приклад 1 1. У земних умовах вода, нагріта до температури 100 °С, набуває стану кипіння. 2. Якщо в урні міститься 10 однакових кульок, пронумерованих від 1 до 10, то кулька, навмання взята із цієї урни, має номер, що міститься в межах від 1 до 10. Подія називається неможливою, якщо в результаті експерименту, проведеного з додержанням певного комплексу умов, вона не настає ніколи. Неможлива подія позначається символом Æ (порожня множина). Приклад 2 1. В урні міститься 10 однакових кульок, пронумерованих від 1 до 10. Навмання береться одна кулька. Поява кульки з номером 12 буде подією неможливою. 2. Якщо на дослідній ділянці посіяти 100 зернин ячменю, то подія, котра полягає в тому, що на момент збирання врожаю на цій ділянці з’явиться колосок пшениці, є неможливою. Подія називається випадковою, якщо за певного комплексу умов у результаті експерименту вона може настати або не настати залежно від дії численних дрібних факторів, урахувати які дослідник не в змозі. Випадкові події позначають символами А, В, С, … або А1, А2, А3,…, Аk; В1, В2, …, Вn. Отже, випадкові події пов’язані експериментами, наслідки яких є неоднозначними. Приклад 3 1. Монету підкидають один раз. (Тут і далі припускаємо, що падає монета на рівну і тверду підлогу.) Поява герба (цифри) — подія випадкова. 2. Якщо на дослідній ділянці в лабораторних умовах посіяно 100 зернин ячменю, то не можна передбачити наперед, скільки зернин проросте. Отже, подія, яка полягає в тому, що проросте від 1 до 100 зернин, є випадковою. 1. Прості та складені випадкові події. Теорія ймовірностей як один із розділів математики досліджує певний вид математичних моделей — моделі випадкових подій, а не самі такі події. Математичні моделі, як відомо, відбивають найістотніші властивості досліджуваних об’єктів, абстрагуючись від неістотних. Для математичного опису випадкових подій — наслідків експерименту — застосовують такі точні поняття: прості (елементарні) та складені випадкові події, простір елементарних подій. Подія, що може відбутися внаслідок проведення однієї і лише однієї спроби (експерименту), називається простою (елементарною) випадковою подією. Елементарні події позначаються wі (і = 1, 2, 3,…) і в теорії ймовірностей, так само як, скажімо, точка в геометрії, не поділяються на простіші складові. Приклад 1. Монету підкидають один раз. Визначити елементарні події цього експерименту. Розв’язання. Можливі такі елементарні випадкові події: w1 = г (монета випаде гербом); w2 = ц (монета випаде цифрою). Приклад 2. Монету підкидають тричі. Визначити елементарні події цього експерименту. Розв’язання. Триразове підкидання монети — це одна спроба. Елементарними випадковими подіями будуть: w1 = ггг (тричі випаде герб); w2 = ццц (тричі випаде цифра);
w4 = гцг (герб випаде двічі); w5 = цгг
w7 = цгц (герб випаде один раз). w8 = ццг Отже, цьому експерименту відповідають вісім елементарних подій. Приклад 3. Задано дві множини цілих чисел W1 = w1 = 1; 1; w5 = 2; 1; w9 = 3; 1; w2 = 1; 2; w6 = 2; 2; w10 = 3; 2; w3 = 1; 3; w7 = 2; 3; w11 = 3; 3; w4 = 1; 4; w8 = 2; 4; w12 = 3; 4. Випадкова подія називається складеною, якщо її можна розкласти на прості (елементарні) події. Складені випадкові події позначаються латинськими великими літерами: A, B, C, D, … . Приклад 4. Задано множину чисел W = {1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12}. Навмання із цієї множини беруть одне число. Побудувати такі випадкові події: 1) з’явиться число, кратне 2; 2) число кратне 3; 3) число, кратне 5. Ці випадкові події будуть складеними. Позначимо їх відповідно А, В, С. Тоді А = Елементарні випадкові події wі Î A, wj Î B, wk Î C, які належать відповідно складеним випадковим подіям А, В, С, тобто є елементами цих множин, називають елементарними подіями, які сприяють появі кожної із зазначених подій унаслідок проведення експерименту (wі сприяють появі події А, wj — події В, wk — події С). Кожному експерименту (спробі) з випадковими результатами (наслідками) відповідає певна множина W елементарних подій wi, кожна з яких може відбутися (настати) внаслідок його проведення: wі Î W. Множину називають простором елементарних подій. Приклад 5. Гральний кубик, кожна грань якого позначена певною цифрою від 1 до 6, підкидають один раз. При цьому на грані випадає одна із зазначених цифр. Побудувати простір елементарних подій для цього експерименту (множину Ώ) і такі випадкові події: 1) А — випаде число, кратне 2; Розв’язання. Оскільки кубик має шість граней, то в результаті експерименту може випасти одна із цифр від 1 до 6. Отже, Ώ = {1, 2, 3, 4, 5, 6}; 1) А = {2, 4, 6}; 2) В = {3, 6}. Приклад 6. Монету підкидають чотири рази. Побудувати простір елементарних подій для цього експерименту і такі випадкові події: 1) А — герб випаде двічі; 2) В — герб випаде не менш як тричі. Розв’язання. Шуканий простір елементарних подій: Ώ = {гггг, гггц, ггцг, гцгг, ццгг, ггцц, гццг, гцгц, цгцг, ццгг, цггц, гццц, цгцц, ццгц, цццг, цццц}; 1) А = {ггцц, ццгг, гцгц, цгцг, гццг, цггц}; 2) В = {гггг, гггц, ггцг, гцгг, цггг). Простір елементарних подій може бути як дискретним, так і неперервним. Якщо множина є зчисленною (зліченною), тобто всі її елементи можна перелічити або принаймні пронумерувати (кожній елементарній події поставити у відповідність один і тільки один елемент нескінченної послідовності натуральних чисел 1, 2, 3, …), то простір елементарних подій називають дискретним. Він може бути обмеженим і необмеженим. У противному разі (тобто коли кожній елементарній події не можна поставити у взаємно однозначну відповідність певне натуральне число) простір елементарних подій називають неперервним. У розглянутих раніше прикладах простори елементарних подій були дискретними. Приклади неперервних (недискретних) просторів елементарних подій дістанемо, розглянувши: 1) розміри однотипних деталей (діаметр, довжина), що їх виготовляє робітник або верстат-автомат; 2) покази приладів, що вимірюють масу, силу струму, напругу, опір і т. ін. Отже, поняття елементарної події, простору елементарних подій є основними в теорії ймовірностей, як точка та пряма в аксіоматично побудованій евклідовій геометрії. Сама природа елементарних подій у теорії ймовірностей при цьому неістотна. Простір елементарних подій є математичною моделлю певного ідеалізованого експерименту в тому розумінні, що будь-який можливий його наслідок описується однією і лише однією елементарною подією — наслідком експерименту. Мовою теорії множин випадкова подія А означується як довільна непорожня підмножина множини W (А Ì W). Операції над подіями üДодавання. Сумою двох подій А і В називається така подія С = А
Рис. 1 Операція А üМноження. Добутком двох подій А і В називається така подія С = А Операція А
Рис. 2 üВіднімання. Різницею двох подій А і В називається така подія
Рис. 3 Приклад. Задано множину цілих чисел Ώ = {1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15}. Навмання з неї беруть одне число. Побудувати випадкові події: 1) А — узяте число кратне 2; Визначити А Розв’язання. 1) А = {2, 4, 6, 8, 10, 12, 14}; 2) В = {3, 6, 9, 12, 15}. Звідси дістаємо: А А∩В = {2, 4, 6, 8, 10, 12, 14} ∩ {3, 6, 9, 12, 15} = {6, 12}; А \ В = {2, 4, 6, 8, 10, 12, 14} \ {3, 6, 9, 12, 15} = {2, 4, 8, 10, 14}. Якщо А∩В ¹ Æ, то випадкові події А і В називають сумісними. Якщо А∩В = Æ, то такі випадкові події А і В називають несумісними. Повна група подій. Протилежні події. Якщо А1 Приклад. При одноразовому підкиданні грального кубика обов’язково з’явиться одна із цифр, що є на його гранях, а саме: А1 = 1, А2 = 2, А3 = 3, А4 = 4, А5 = 5, А6 = 6. Отже, випадкові події Аі (і = Дві несумісні випадкові події, що утворюють повну групу, називають протилежними. Подія, яка протилежна А, позначається
Рис. 4 Випадкові події А, В, С (А Ì Ω, В
8. А 9. А 10. А 11. А 12. 13. 14. 15. А 16. 17. Елементарні випадкові події задовольняють такі твердження: 1) між собою несумісні; 2) утворюють повну групу; 3) є рівноможливими, а саме: усі елементарні події мають однакові можливості відбутися внаслідок проведення одного експерименту. Для дискретного простору Ω перші два твердження можна записати так: 1) ωі Для кількісного вимірювання появи випадкових подій і їх комбінацій уводиться поняття ймовірності події, що є числом такої ж природи, як і відстань у геометрії або маса в теоретичній механіці. Класичне означення ймовірності Імовірністю випадкової події А називається невід’ємне число Р(А), що дорівнює відношенню числа елементарних подій m (0 Р (А) = Для неможливої події Р (Æ) = 0 (m = 0); Для вірогідної події Р (Ω) = 1 (m = n). Отже, для довільної випадкової події
Приклад 1. У ящику міститься 15 однотипних деталей, із яких 6 бракованих, а решта — стандартні. Навмання з ящика береться одна деталь. Яка ймовірність того, що вона буде стандартною? Розв’язання. Число всіх рівноможливих елементарних подій для цього експерименту: n = 15. Нехай А — подія, що полягає в появі стандартної деталі. Число елементарних подій, що сприяють появі випадкової події А, дорівнює дев’яти
Приклад 2. Гральний кубик підкидають один раз. Яка ймовірність того, що на грані кубика з’явиться число, кратне 3? Розв’язання. Число всіх елементарних подій для цього експерименту n = 6. Нехай В — поява на грані числа, кратного 3. Число елементарних подій, що сприяють появі В, дорівнює двом (m = 2). Отже,
Приклад 3. Два гральні кубики підкидають по одному разу. Побудувати простір елементарних подій — множину Ώ і такі випадкові події: А — сума цифр виявиться кратною 4; В — сума цифр виявиться кратною 3. Обчислити Р (А), Р (В), Р (А Розв’язання. Простір елементарних подій — множину W запишемо у вигляді таблиці:
Отже, простір елементарних подій W містить n = 36 пар чисел. Події А і В визначимо з допомогою побудованої таблиці так: елементарні події, які сприяють появі А (сума цифр кратна 4), заштриховані вертикальними лініями, а для В (сума кратна 3) — горизонтальними лініями. Звідси маємо: число елементарних подій, що сприяють появі А, дорівнює дев’яти (m1 = 9), а число елементарних подій, що сприяють появі В, — дванадцяти (m2 = 12), число елементарних подій, що сприяють появі події А Остаточно дістаємо:
Приклад 4. У кожній із трьох урн містяться червоні та сині кульки. Із кожної урни навмання беруть по одній кульці. Побудувати простір елементарних подій для цього експерименту — множину W і такі випадкові події: А — серед трьох навмання взятих кульок дві виявляються червоного кольору; В — серед трьох кульок дві виявляються синього кольору. Обчислити Р (А), Р (В), Р (А Розв’язання. Позначимо появу кульки червоного кольору як Ч, а синього кольору як С. Тоді простір елементарних подій буде такий: = {ЧЧЧ, ЧЧС, ЧСЧ, СЧЧ, ЧСС, СЧС, ССЧ, ССС}, n = 8. Події: А = {ЧЧС, ЧСЧ, СЧЧ}, m1 = 3; В = {ССЧ, СЧС, ЧСС}, m2 = 3. Події А і В є несумісними (А Обчислюємо: Приклад 5. В електричну мережу увімкнено чотири електролампочки. При проходженні електричного струму в мережі кожна електролампочка із певною ймовірністю може перегоріти або не перегоріти. Побудувати простір елементарних подій (множину W) — числа електролампочок, які не перегорять, і такі випадкові події: А — із чотирьох електролампочок перегорять не більш як дві; В — не менш як три. Обчислити Р (А), Р (В), Р (А Розв’язання. Нехай Аi (і = W = {А1 А2 А3 А4, А1 А2 А3 Випадкові події: А = {А1 А2 В = {А1 А2 А
4. Елементи комбінаторики При розв’язуванні задач з теорії ймовірностей побудувати простір елементарних подій (множину W) можна не завжди. Для більшості прикладних задач така побудова пов’язана з виконанням великого обсягу робіт, а нерідко й взагалі неможлива. Щоб обчислити ймовірність тієї чи іншої випадкової події для певного класу задач із дискретним і обмеженим простором елементарних подій, необхідно вміти обчислити кількість n усіх елементарних подій (елементів множини W) і число m елементарних подій, які сприяють появі випадкової події. Існує клас задач, в яких для обчислення n і m використовуються елементи комбінаторики: переставлення, розміщення та комбінації. У комбінаториці оперують множинами однотипних елементів. Загалом множини бувають упорядковані та невпорядковані. Множину називають упорядкованою, якщо при її побудові істотним є порядок розміщення елементів. У противному разі множину називають невпорядкованою. Переставлення. Переставленням із n елементів називають такі впорядковані множини з n елементів, які різняться між собою порядком їх розміщення. Кількість таких упорядкованих множин обчислюється за формулою
де n набуває лише цілих невід’ємних значень. Оскільки 1! = 0! Отже, 0! = 1. Приклад 1. На кожній із шести однакових карток записано одну з літер Я, І, Р, Е, О, Т. Яка ймовірність того, що картки, навмання розкладені в рядок, утворять слово
Розв’язання. Кількість усіх елементарних подій (елементів множини Ω) n = 6! = 6 × 5 × 4 × 3 × 2 × 1 = 720. Кількість елементарних подій, що сприяють появі слова ТЕОРІЯ,
Приклад 2. Задано множину цілих чисел Ω = {1, 2, 3, 4, 5}. Її елементи навмання розставляють у рядок. Обчислити ймовірності таких випадкових подій: А — розставлені в ряд числа утворюють зростаючу послідовність; В — спадну послідовність; С — цифра 1 стоятиме на першому місці, а 5 — на останньому; D — цифри утворять парне п’ятицифрове число. Розв’язання. Простір елементарних подій для цього експерименту міститиме n = 5! = 1 × 2 × 3 × 4 × 5 = 120 несумісних, рівноймовірних елементарних подій. Кількість елементарних подій, що сприяють появі А, дорівнює одиниці (m1 = 1). Кількість елементарних подій, що сприяють появі В, дорівнює одиниці (m2 = 1). Для випадкової події С m3 = 3! Для випадкової події D m4= 4! 2 = 48. Обчислюємо:
Розміщення. Розміщенням із n елементів по m (0 Кількість таких множин обчислюється за формулою
Наприклад, Приклад 1. Маємо дев’ять однакових за розміром карток, на кожній з яких записано одну з цифр: 1, 2, 3, 4, 5, 6, 7, 8, 9. Навмання беруть чотири картки і розкладають в один рядок. Яка ймовірність того, що при цьому дістанемо
Розв’язання. Кількість елементарних подій множини W буде Кількість елементарних подій, що сприяють появі 1, 9, 7, 3, дорівнює одиниці (m = 1). Позначимо цю випадкову подію через В. Тоді
Приклад 2. У кімнаті перебувають 10 студентів. Яка ймовірність того, що два і більше студентів не мають спільного дня народження? Розв’язання. Вважаємо, що рік має 365 днів. Для кожного студента в загальному випадку існує 365, а для 10 студентів — 36510 можливих днів народження. Отже, маємо n = 36510 елементарних подій множини Ω. Позначимо через В випадкову подію, яка полягає в тому, що дні народження студентів не збігаються. Кількість елементарних подій, що сприяють появі В, Остаточно маємо: Комбінації. Комбінаціями з n елементів по Кількість таких множин
Приклад 1. У цеху працює 10 верстатів-автоматів, кожний із яких може з певною ймовірністю перебувати в роботоздатному стані або в стані поломки. Яка ймовірність того, що під час роботи верстатів-автоматів із ладу вийдуть три з них? Розв’язання. Оскільки кожний верстат-автомат може перебувати у двох несумісних станах — роботоздатному або нероботоздатному, то кількість усіх елементарних подій множини Ω буде n = 210. Позначимо через А випадкову подію — із ладу вийде три верстати з десяти. Тоді кількість елементарних подій, що сприяють появі А, буде
Отже,
Приклад 2. У шухляді міститься 10 одинотипних деталей, 6 із яких є стандартними, а решта бракованими. Навмання із шухляди беруть чотири деталі. Обчислити ймовірність таких випадкових подій: А — усі чотири деталі виявляються стандартними; В — усі чотири деталі виявляються бракованими; D — із чотирьох деталей виявляються дві стандартними і дві бракованими. Розв’язання. Кількість усіх елементарних подій множини Ω
кількість елементарних подій, що сприяють події А:
кількість елементарних подій, що сприяють появі В:
кількість елементарних подій, що сприяють появі D:
Обчислимо ймовірності цих подій:
Поиск по сайту: |
 w3 = ггц
w3 = ггц , W2 =
, W2 =  . Із кожної множини навмання беруть по одному числу. Визначити елементарні події цього експерименту — появу пари чисел.
. Із кожної множини навмання беруть по одному числу. Визначити елементарні події цього експерименту — появу пари чисел. В (С = А + В), яка внаслідок експерименту настає з настанням принаймні однієї з подій А або В. Подію А
В (С = А + В), яка внаслідок експерименту настає з настанням принаймні однієї з подій А або В. Подію А 
 В (С = АВ), яка внаслідок експерименту настає з одночасним настанням подій А і В.
В (С = АВ), яка внаслідок експерименту настає з одночасним настанням подій А і В.

 A2
A2  = W, то такі випадкові події утворюють повну групу, а саме: внаслідок експерименту якась із подій Аі обов’язково настане.
= W, то такі випадкові події утворюють повну групу, а саме: внаслідок експерименту якась із подій Аі обов’язково настане.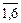 ) утворюють повну групу:
) утворюють повну групу:  = Ω =
= Ω =  . Протилежні події у просторі елементарних подій ілюструє рис. 4. Він унаочнює також співвідношення: А
. Протилежні події у просторі елементарних подій ілюструє рис. 4. Він унаочнює також співвідношення: А  = Ω, А∩
= Ω, А∩ 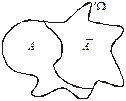
 Ω, С
Ω, С 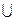 А = А, А
А = А, А 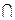 А = А.
А = А.
 В = В
В = В  = Æ.
= Æ.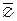 = Ω.
= Ω.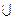 (А
(А 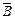 ) = А; В = В
) = А; В = В 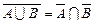 .
.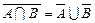 .
.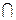 ωj = Æ, і
ωj = Æ, і  ј; 2)
ј; 2)  = Ω.
= Ω. m
m 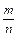 . (1)
. (1) . (2)
. (2)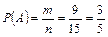 .
. .
. .
.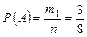 ;
; 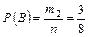 ; Р (А
; Р (А 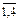 ) відповідно першу, другу, третю та четверту електролампочку, що не перегорять, а
) відповідно першу, другу, третю та четверту електролампочку, що не перегорять, а 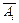 — що перегорять. Тоді простір елементарних подій буде:
— що перегорять. Тоді простір елементарних подій буде: А1 А2
А1 А2  А4, А1
А4, А1  А3 А4,
А3 А4,  А2 А3 А4, А1 А2
А2 А3 А4, А1 А2 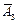
 ,
, 
 А3 А4,
А3 А4, 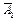 А2
А2  А4, А1
А4, А1  А3
А3 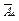 , А1
, А1 
 А4,
А4,  А2 А3
А2 А3  , А1
, А1  ,
, 
 А3
А3 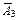 А4,
А4,  ;
; 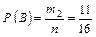 ;
;  .
. , (3)
, (3) , то при n = 1 маємо
, то при n = 1 маємо .
. ;
;  ;
; ;
;  .
. ) називаються такі впорядковані множини, кожна із яких містить m елементів і які відрізняються між собою порядком розташування цих елементів або хоча б одним елементом.
) називаються такі впорядковані множини, кожна із яких містить m елементів і які відрізняються між собою порядком розташування цих елементів або хоча б одним елементом. . (4)
. (4) .
. .
. .
.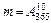 .
. .
.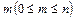 називаються такі множини з m елементів, які різняться між собою хоча б одним елементом.
називаються такі множини з m елементів, які різняться між собою хоча б одним елементом. . (5)
. (5) .
. .
. ;
; ;
; ;
;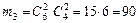 .
. ;
; ;
; .
.