 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Аксіоми теорії ймовірностей та їх наслідки
Загалом функції дійсних змінних бувають визначеними не на всій множині дійсних чисел, а лише на певній її підмножині, яку називають областю визначення функції. Імовірність також не завжди можна визначити для будь-яких підмножин множини Ω (простору елементарних подій). Тому доводиться обмежуватися певним класом підмножин, до якого висуваються вимоги замкненості відносно операцій додавання, множення та віднімання. Нехай задано довільний простір елементарних подій — множину Ω і Q — деяка система випадкових подій. Система подій називається алгеброю подій, якщо: 1. Ώ Î Q. 2. Із того, що А Î Q, В Î Q, випливає: що А Із тверджень 1 і 2 дістаємо, що Ø = Ώ \ Ώ, а отже, Ø Ì Q. Найменшою системою, яка буде алгеброю подій, є Q = (Ø, Ώ). Якщо Ώ — обмежена множина, то система Q також буде обмеженою. Якщо множина містить n елементів, то кількість усіх підмножин буде 2n. Якщо Ω є неперервною множиною, то система Q утворюється квадровними підмножинами множини Ω, які також утворюють алгебру подій. Числова функція Р, що визначена на системі подій Q, називається ймовірностю, якщо: 1. Q є алгеброю подій. 2. Для будь-якого А Ì Q існує 3. Р (Ω) = 1. 4. Якщо А і В є несумісними (А
Для розв’язування задач з нескінченними послідовностями подій, наведені аксіоми необхідно доповнити аксіомою неперервності. 5. Для будь-якої спадної послідовності
Трійка (Q, Ω, Р), де Q є алгеброю подій і Р задовольняє аксіоми 1—5, називається простором імовірностей. Приклад 1. Задано множину цілих чисел Ω = {1, 2, …, 30}. Навмання з цієї множини беруть одне число. Яка ймовірність того, що воно виявиться кратним 5 або 7? Розв’язання. Простір Ω містить n = 30 елементарних подій. Позначимо через А подію, що полягає в появі числа, кратного 5, а через В у появі числа, кратного 7. Тоді дістанемо:
Згідно з (6) маємо:
Приклад 2. Садівник восени посадив 10 саджанців яблуні. Кожний із саджанців може прийнятись або не прийнятись із певною ймовірністю. Яка ймовірність того, що з 10 саджанців навесні наступного року приймуться 6 або 2? Розв’язання. Множина Ω містить n = 210 елементарних подій. Нехай А — випадкова подія, яка полягає в тому, що число саджанців, котрі проросли, дорівнює 6; В — число саджанців, що проросли, дорівнює 2. Кількість елементарних подій, які сприяють появі А:
Кількість елементарних подій, що сприяють появі В:
Оскільки А
Приклад 3. У ящику міститься 13 однакових деталей, серед яких 5 є бракованими, а решта — стандартними. Навмання з ящика беруть чотири деталі. Яка ймовірність того, що всі чотири деталі виявляться стандартними або бракованими? Розв’язання. Множина Ω містить Згідно з (6) дістанемо:
Наслідки аксіом 1. Якщо випадкові події А1, А2, А3, … Аn є несумісними попарно, то
2. Якщо випадкові події А1, А2, А3, … Аn утворюють повну групу, то
Із рівності А
Якщо
Справді:
Оскільки
Отже,
3. Формула додавання для n сумісних випадкових подій має такий вигляд:
Наприклад, для трьох сумісних випадкових подій формулу (12) можна записати так:
4. Якщо випадкова подія А сприяє появі
Приклад 1. В урні містяться 30 однакових кульок, які пронумеровані від 1 до 30. Навмання із урни беруть одну кульку. Яка ймовірність того, що номер кульки виявиться кратним 3 або 5? Розв’язання. Кількість усіх елементарних подій множини Ω n = 30. Позначимо через А = {3, 6, 9, 12, 15, 18, 21, 24, 27, 30} (m1 = 10) —
Згідно з (10) дістанемо
Приклад 2. Чотири спортсмени мають виконати норму майстра спорту. Кожний із них може виконати її із певною ймовірністю. Яка ймовірність того, що із чотирьох спортсменів норму майстра спорту виконують не менш як два спортсмени; не більш як три? Розв’язання. Позначим через А1 А2 А3 А4 випадкові події, що відповідно перший, другий, третій та четвертий спортсмени виконають норму майстра, а через W = {А1 А2 А3 А4, А1 А2 А3 Випадкові події: А = {А1 А2 В = {А1 А2 А3 А Шукана ймовірність:
Приклад 3. Випадкові події А1, А2, А3, А4 є попарно несумісними і утворюють повну групу. Знайти Р (А1), Р (А2), Р (А3), Р (А4), коли відомо, що Р (А1) = 0,2 Р (А2), Р (А2) = 0,8 Розв’язання. Оскільки випадкові події А1, А2, А3, А4 є попарно несумісними і утворюють повну групу, то згідно з (8) дістаємо:
За умовою задачі знаходимо: Р (А2) = 0,8 Р (А3) = 0,8 × 0,5 Р (А4) = 0,4 Р (А4). Р (А1) = 0,2 Р (А2) = 0,2 × 0,4 (А4) = 0,08 Р (А4). Отже, 0,08 Р (А4) + 0,4 Р (А4) + 0,5 Р (А4) + Р (А4) = 1;
Поиск по сайту: |
 В Î Q , А
В Î Q , А  В Î Q, А \ В Î Q.
В Î Q, А \ В Î Q. .
. . (6)
. (6) подій із Q, такої, що
подій із Q, такої, що  Ø, випливає рівність
Ø, випливає рівність .
. ;
; ;
; Ø.
Ø. .
. .
. .
. .
.
 . Позначимо через В появу чотирьох бракованих деталей. Кількість елементарних подій, що сприяють появі В,
. Позначимо через В появу чотирьох бракованих деталей. Кількість елементарних подій, що сприяють появі В,  .
.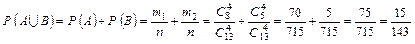 .
. . (7)
. (7) . (8)
. (8) = Ω і аксіом 3, 4 випливає, що
= Ω і аксіом 3, 4 випливає, що
 . (9)
. (9) Ø, то
Ø, то . (10)
. (10) , то
, то 
 Ø). (11)
Ø). (11) і при цьому
і при цьому  = Ø, то
= Ø, то
 .
. (12)
(12)
 . (13)
. (13) , то
, то . (14)
. (14) є подіями сумісними.
є подіями сумісними. .
. — відповідно випадкові події, що перший, другий, третій та четвертий спортсмени не виконають норму. Тоді простір елементарних подій для цього експерименту буде:
— відповідно випадкові події, що перший, другий, третій та четвертий спортсмени не виконають норму. Тоді простір елементарних подій для цього експерименту буде: , А1 А2
, А1 А2  А4, А1
А4, А1  А3 А4,
А3 А4,  А2 А3 А4, А1 А2
А2 А3 А4, А1 А2  .
. .
. ;
; ;
; ;
; .
.