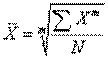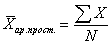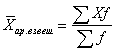Методические указания и решение типовых задач

Средние величины И показатели вариации

Средней величиной называют показатель, который характеризует обобщенное значение признака или группы признаков в исследуемой совокупности. Средние величины используются на этапе обработки и обобщения полученных первичных статистических данных. Потребность определения средних величин связана с тем, что у различных единиц исследуемых совокупностей индивидуальные значения одного и того же признака, как правило, неодинаковы.Если исследуется совокупность с качественно однородными признаками, то средняя величина выступает здесь как типическая средняя.

Понятие и виды средних величин. Средняя величина - это обобщающий показатель статистической совокупности, который погашает индивидуальные различия значений статистических величин, позволяя сравнивать разные совокупности между собой. Существует 2 класса средних величин: степенные и структурные.

К структурным средним относятся мода и медиана, но наиболее часто применяются степенные средние различных видов.

Степенные средние величины.Степенные средние могут быть простыми и взвешенными.Простая средняя величина рассчитывается при наличии двух и более несгруппированных статистических величин, расположенных в произвольном порядке по следующей общей формуле:

Взвешенная средняя величина рассчитывается по сгруппированным статистическим величинам с использованием следующей общей формулы:

где X – значения отдельных статистических величин или середин группировочных интервалов;
m - показатель степени, от значения которого зависят следующие виды степенных средних величин:
при m = -1 средняя гармоническая;
при m = 0 средняя геометрическая;
при m = 1 средняя арифметическая;
при m = 2 средняя квадратическая;
при m = 3 средняя кубическая.

Главным условием, при котором можно использовать степен­ные средние в статистическом анализе, является однородность со­вокупности, т.е. она не должна содержать исходные данные, рез­ко отличающиеся по своему количественному значению (в лите­ратуре они носят название аномальных наблюдений).

Продемонстрируем важность этого условия на следующем примере. Допустим, вычисляется средняя заработная плата рабо­тающих на малом предприятии :

Таблица 6.1

Тогда средний размер заработной платы составит:

А теперь предположим, что в нашу совокупность добавился всего лишь один человек, но с окладом в 50000 руб. (очевидно, это директор предприятия). В таком случае вычисляемая средняя будет совсем другая:

Как видим, значение средней превышает 7000 руб., т. е. она больше всех значений признака за исключением одного единственного наблюдения, Для того чтобы таких случаев не проис­ходило на практике, и средняя не теряла бы своего смысла (в дан­ном примере она уже не выполняет роль обобщающей характе­ристики совокупности, которой должна быть), при расчете сред­ней следует аномальные, резко выделяющиеся наблюдения либо исключить из анализа и тем самым сделать совокупность одно­родной, либо разбить совокупность на однородные группы и вычислить средние значения по каждой группе и анализировать не общую среднюю, а среднегрупповые значения.

Средняя арифметическая.Средняя арифметическая - это самая часто используемая средняя величина, которая получается, если подставить в общую формулу m=1. Средняя арифметическая простая имеет следующий вид:

где X - значения величин, для которых необходимо рассчитать среднее значение; N - общее количество значений X (число единиц в изучаемой совокупности).
Например, предположим, что у нас имеются данные о величине рентабель­ности по 10 малым предприятиям (%):10, 12, 12, 15, 15, 15, 17, 17,20,20.

Тогда средняя рентабельность составит:

Средняя арифметическая взвешенная имеет следующий вид:

где f - количество величин с одинаковым значением X (частота).

Теперь обобщим (систематизируем) наши данные, для чего сгруппируем их .Запишем выражение для вычисления среднего уровня рента­бельности в табличной форме:

Таблица 6.2

Поиск по сайту: