 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Математичні моделі деяких ситуацій та процесів
Приклад 1. (Закон природного зростання). Законом природного зростання називають такий закон, за яким швидкість зростання речовини пропорційна кількості речовини. Треба знайти формулу для визначення кількості речовини у будь-який момент часу, якщо відомо, що у початковий момент часу, тобто при Розв’язання. Позначимо через
де За умовою задачі повинна виконуватись рівність
Отже, математична модель закону природного зростання речовини є задача Коші для диференціального рівняння першого порядку вигляду (1)з початковою умовою вигляду (2). Рівняння (1)досить просте, тому можна знайти його загальний розв'язок. Дійсно, рівняння (1)можна записати у вигляді
Якщо диференціали двох функцій рівні, то функції можуть відрізнятись лише довільною сталою, тому
Звідси, потенціюванням знаходимо
Формула (3)дає вираз для кількості речовини як функції часу. Вона містить довільну сталу Використовуючи початкові умови (2),одержимо:
Отже, формула (3)тепер буде мати вигляд
Це і є шукана формула. За законом природного зростання (4)зростає кількість живих клітин, кристалів, населення. Приклад 2. (Закон радіоактивного розпаду). Відомо, що радіоактивний розпад речовини здійснюється так: швидкість розпаду речовини у будь-який момент часу пропорційна кількості речовини, що не розпалась. Треба знайти формулу, за якою можна визначити кількість речовини Розв'язання. Використовуючи механічний зміст похідної та умову задачі, закон радіоактивного розпаду речовини можна записати у вигляді
де коефіцієнт Рівняння (5)аналогічне рівнянню (1)і тому можна записати шукану формулу у вигляді
Приклад 3. (Рівняння руху). Нехай матеріальна точка Розв'язання. Згідно з механічним змістом похідних першого та другого порядків, вектор
є швидкість, а вектор
є прискоренням руху точки За законом Ньютона
де сила Рівняння (7)називають основним рівнянням механіки. Це рівняння еквівалентне трьом рівнянням у координатній формі
Отже, одержали, що математична модель руху є диференціальне рівняння другого порядку (7)або система диференціальних рівнянь (8). Приклад 4. (Зростання інвестицій). Економісти встановили, що швидкість зростання інвестованого капіталу у будь-який момент часу Розв'язання. Спочатку побудуємо математичну модель цієї задачі. Позначимо: тоді За умовою задачі маємо:
Одержали задачу Коші для диференціального рівняння першого порядку аналогічного рівнянню (1). Тому загальним розв'язком диференціального рівняння буде функція
Згідно з початковою умовою при
Отже, розв'язком задачі Коші (9)буде функція
Це означає, що при умовах задачі інвестиції з часом зростають за експоненціальним законом.
Поиск по сайту: |
 , кількість речовини дорівнювала
, кількість речовини дорівнювала  .
. шукану кількість речовини в момент
шукану кількість речовини в момент 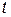 . Тоді швидкість зростання речовини є швидкість зміни функції
. Тоді швидкість зростання речовини є швидкість зміни функції 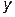 . Згідно з механічним змістом похідної та умовою задачі закон природного зростання речовини можна записати у вигляді
. Згідно з механічним змістом похідної та умовою задачі закон природного зростання речовини можна записати у вигляді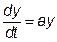 ,(1)
,(1) – коефіцієнт пропорційності.
– коефіцієнт пропорційності. . (2)
. (2) або
або 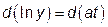 .
. .
. . (3)
. (3) , яка може приймати довільні числові значення. Тому формула (3)дає не один, а нескінченну кількість розв'язків задачі.
, яка може приймати довільні числові значення. Тому формула (3)дає не один, а нескінченну кількість розв'язків задачі. .
. . (4)
. (4)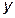 , яка ще не розпалась, у будь-який момент часу
, яка ще не розпалась, у будь-який момент часу  , (5)
, (5) від'ємний тому, що функція
від'ємний тому, що функція  . (6)
. (6) масою
масою  рухається в просторі. Радіус-вектор цієї точки позначимо
рухається в просторі. Радіус-вектор цієї точки позначимо  . Координати точки
. Координати точки 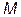 є і координатами радіус-вектора
є і координатами радіус-вектора  у вигляді функції часу
у вигляді функції часу 

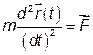 , (7)
, (7) .
.

 . (8)
. (8) неперервного зростання капіталу. Треба знайти закон зростання інвестованого капіталу, враховуючи величину початкової
неперервного зростання капіталу. Треба знайти закон зростання інвестованого капіталу, враховуючи величину початкової  інвестиції
інвестиції  .
. – величина інвестованого капіталу у момент
– величина інвестованого капіталу у момент  – швидкість зміни величини інвестиції,
– швидкість зміни величини інвестиції,  .
. . (9)
. (9) . (10)
. (10) .
. . (11)
. (11)