 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Основні поняття та задачі теорії диференціальних рівняньСтр 1 из 3Следующая ⇒
Міністерство освіти і науки України Державний університет ТеЛЕКОМУНІКАЦІЙ
КАФЕДРА ВИЩОЇ МАТЕМАТИКИ ЗАТВЕРДЖУЮ Завідуючий кафедрою ________________Барабаш О.В. “ ____ “ _____________ 2015 року
Тільки для викладачів СЕМЕСТР 2 Л Е К Ц І Я № 1(19) МОДУЛЬ 1(4) Тема 1(8): „Звичайні диференціальні рівняння” Основні поняття та задачі теорії диференціальних рівнянь. Теорема про існування розв’язку задачі Коші. Розв’язування ДР першого порядку: з відокремленими змінними та подільними змінними, однорідних, лінійних, Бернуллі.
з навчальної дисципліни вища математика
напряму підготовки телекомунікації
освітньо-кваліфікаційного рівня бакалавр Лекція розроблена кандидатом фіз.-мат. наук, доцентом Онищенко В.В.
Обговорено на засіданні кафедри (ПМК) Протокол № __________ “ ____ “ _____________ 2015 року
Київ – 2015
Навчальні цілі: Ознайомити студентів з основними поняттями та задачами теорії диференціальних рівнянь, з правилами та методами ДР першого порядку: з відокремленими змінними, однорідними, лінійними, Бернуллі.
Виховні цілі:Обґрунтувати, що якісне вивчення математичного аналізу сприяє: - розвитку логічного та аналітичного мислення, пам’яті; - можливості самостійно вивчати сучасну науково-технічну літературу; - вмінню коротко і зрозуміло висловлювати свої думки; - акуратності і точності записів, уважності, дисциплінованості; - вмінню конспектувати, красиво оформлювати записи робочих зошитів для практичних занять та індивідуальних робіт; - набуттю навичок систематизації матеріалу, що вивчається.
Час:1,5 години.
ПЛАН ПРОВЕДЕННЯ ЛЕКЦІЇ ТА РОЗРАХУНОК ЧАСУ
Введення. Перевірити наявність студентів на лекції 5 хвилин
Навчальні питання: 1. Основні поняття та задачі теорії диференціальних рівнянь 20 хвилин 2. Математичні моделі деяких ситуацій та процесів 10 хвилин 3. Диференціальні рівняння з відокремлюваними змінними 15 хвилин 4. Однорідні диференціальні рівняння першого порядку 15 хвилин 5. Рівняння лінійні та Бернуллі 20 хвилин
Заключення5 хвилин
НАВЧАЛЬНО-МАТЕРІАЛЬНЕ ЗАБЕЗПЕЧЕННЯ Бажано мати: 1. крейду і вологу губку;
НАВЧАЛЬНІ МАТЕРІАЛИ
ТЕКСТ ЛЕКЦІЇ ЗВИЧАЙНІ ДИФЕРЕНЦІАЛЬНІ РІВНЯННЯ Основні поняття та задачі теорії диференціальних рівнянь.
Означення 1. Звичайними диференціальними рівняннями називають такі рівняння, які містять шукану функцію однієї змінної та її похідні або диференціали. Це означення у загальному вигляді математично можна записати так
Означення 2. Найвищий порядок похідної, що містить диференціальне рівняння, називають порядком диференціальногорівняння. Наприклад, рівняння Означення 3. Загальним розв'язком диференціального рівняння Загальний розв'язок диференціального рівняння може бути і не розв'язаним відносно Означення 4. Якщо у загальному розв'язку (інтегралі) диференціального рівняння замість довільних сталих записати фіксовані постійні числа, то одержаний розв'язок називають частиннимрозв'язком цього рівняння. Найчастіше сталі Означення 5. Сумісне завдання диференціального рівняння та відповідної кількості початкових умов називають задачею Коші. Наприклад, для диференціального рівняння першого порядку задачу Коші можна записати у вигляді
Для диференціального рівняння другого порядку задачу Коші можна записати у вигляді
У дослідженнях різноманітних життєвих та економічних проблем найчастіше використовують диференціальні рівняння першого та другого порядків певних типів та відповідні їм задачі Коші. В теорії звичайних диференціальних рівнянь можна виділити дві основні задачі: 1) знаходження диференціального рівняння та початкових умов, які описують ситуацію або процес, який досліджують; 2) розв'язування заданої задачі Коші або знаходження загального розв'язку заданого диференціального рівняння. Розглянемо декілька прикладів розв'язування цих основних задач.
Поиск по сайту: |
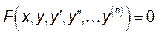 .
.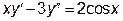 – другого порядку; рівняння
– другого порядку; рівняння  – третього порядку; рівняння
– третього порядку; рівняння 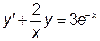 та
та  – першого порядку.
– першого порядку. -го порядку називають функцію
-го порядку називають функцію 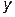 , яка залежить від аргументу
, яка залежить від аргументу  та
та  ,
, 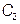 , …,
, …, 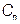 , тобто має вигляд
, тобто має вигляд 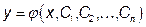 яка, при її підстановці у рівняння, перетворює рівняння у тотожність.
яка, при її підстановці у рівняння, перетворює рівняння у тотожність. . У цьому випадку його називають загальним інтегралом диференціального рівняння.
. У цьому випадку його називають загальним інтегралом диференціального рівняння.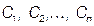 обирають не довільно, а так, щоб розв'язок рівняння задовольняв деяким початковим умовам. Для знаходження я довільних сталих треба задати
обирають не довільно, а так, щоб розв'язок рівняння задовольняв деяким початковим умовам. Для знаходження я довільних сталих треба задати 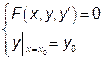 .
. .
.