 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Моделювання стаціонарних систем. Нелінійні системи
Стационарное состояние системы моделируется системой нелинейных уравнений. Если имеем систему с локализованными свойствами, тогда модель представляет собой систему нелинейных конечных (не дифференциальных) уравнений. Если моделируется система с распределенными свойствами, тогда матем. модель будет представлять собой систему дифференциальных уравнений в частных производных (без времени). Рассмотрим методы решения конечных уравнений и их систем, используемые в моделировании. Метод бисекций Для этого метода характерны слабые требования для функции F(x): требуется лишь ее непрерывность. Кроме того, должен быть определен отрезок [a,b] такой, что F(a)×F(b) < 0 . При этих условиях сходимость итерационного процесса гарантируется. Пример уравнения, которое не решается методом бисекций: (x-a)2 = 0 . Пусть [a,b] - начальный отрезок. Абсолютная ea и относительная er погрешности получаемого решения связаны соотношением: ea = er (b-a) . Число обращений к процедуре вычисления F(x), необходимое для получения относительной погрешности er равно:
Методы хорд и случайного поиска в среднем имеют такие же характеристики, как и метод бисекций.
Метод Ньютона Этот метод требует непрерывность функции F(x) и ее производной. Для начала работы итерационного процесса необходимо задать начальное приближение x0. При этом точка x0 должна принадлежать области сходимости, которая определяется свойствами функции F(x). Область сходимости представляет собой некоторую окрестность точки - точного решения уравнения. В отличие от метода бисекций, отсутствует возможность контроля абсолютной погрешности получаемого решения. В качестве меры погрешности используются величины ef, ex , а соответствующие условия завершения итераций имеют вид: |F(xk)| < ef , |xk+1 – xk| < ex . При наличии сходимости, скорость сходимости очень высока. Метод итераций Преобразуем (если это возможно) уравнение (1) к следующему виду: x = G(x) . Запишем итерационную формулу следующим образом:
Метод решения уравнения, основанный на использовании последней итерационной формулы, называется методом итераций. Пусть x – искомое решение, а x0 – начальное приближение. Критерием сходимости процедуры (5) является условие "xÎ[x0,x]: |G¢(x)|<1 . Для контроля погрешности используются такие же условия, как и для метода Ньютона.
Системы нелинейных уравнений Рассмотрим методы решения систем уравнений вида: F(x) = 0 . Метод Ньютона и его модификации. Проблема вырождения Пусть k - номер приближения, обозначим через Dk вектор-приращения для k-того шага: Dk+1 = xk+1 - xk . Величина вектора-приращения находится путем решения СЛУ следующего вида: P(xk)× Dk+1 = -F(xk) , где P(xk) - матрица Якоби для системы уравнений в точке xk . Область сходимости Областью сходимости является R-окрестность точки в пространстве Rn, обладающая свойством: В общем случае чем точнее выбрано начальное приближение, тем выше вероятность попадания в область сходимости. Метод Ньютона-Рафсона Итерационная формула содержит дополнительный параметр lk:
который называется шаговый множитель. Он выбирается из интервала [0,1]. С уменьшением величины шагового множителя область сходимости расширяется, однако скорость сходимости при этом падает. Проблема вырождения В некоторых случаях при выполнении очередного шага может оказаться, что определитель матрицы Якоби равен нулю (вырождение системы). Тогда дальнейший счет по формуле (2) становится невозможным. Вырождение системы может порождаться не только свойствами самой системы, но и машинной погрешностью. Вообще вырождение обычно имеет место для т.н. жестких систем. Контроль погрешности Также, как и в случае решения одного уравнения итерационным методом, условие завершения итераций можно записать одним из двух способов: 1) 2) Здесь k - номер итерации, i - номер компонента соответствующего вектора. Метод градиента Пусть имеем задачу (5.6.1). Рассмотрим следующую функцию:
Решению исходной системы уравнений соответствует точка минимума последней функции. Задача, таким образом, сводится к задаче многомерной оптимизации. Для ее решения часто используют метод градиента (метод кратчайшего спуска), который будет рассмотрен далее.
15. Моделювання динаміки систем. Системи з локалізованими та розподіленими
Уравнения переходных процессов В математическом моделировании все системы делят на системы с сосредоточенными параметрами и системы с распределенными параметрами. Поведение во времени систем первого вида описывается обыкновенными дифференциальными уравнениями (задача Коши). Поведение систем второго типа описывают дифференциальными уравнениями в частных производных. Рассмотрим систему с сосредоточенными параметрами. Для описания динамики такой системы используется система дифференциальных уравнений, которая, в общем случае может быть представлена так:
К этим уравнениям необходимо добавить еще систему начальных условий. Путем соответствующей замены переменных (и ценой увеличения числа уравнений) последнюю систему всегда можно преобразовать так, что она будет содержать производные только лишь первого порядка. С учетом начальных условий задача будет иметь следующий вид:
Решением задачи является набор функций x1(t), x2(t), … , xn(t) . Для численного решения такой задачи могут быть использованы т.н. неявные методы. Довольно часто систему уравнений (1) удается разрешить относительно производных, тогда задача принимает следующий вид:
Такого рода дифференциальную задачу называют задачей Коши. Задачу Коши можно представить в векторной форме:
В дальнейшем значок вектора будем опускать. Будем иметь в виду, что если речь идет о системе уравнений, то x понимается как вектор искомых функций, а F(x,t) – как вектор правых частей системы уравнений. Таким образом, задачу Коши для системы уравнений, так же как и для одного уравнения, будем записывать следующим образом:
Если задача решается численно, всегда задан некоторый конечный интервал интегрирования [0,T] . Для построения алгоритма используется дискретизация по t и конечные разности. Результат численного решения Задачи Коши имеет табличную форму представления искомых функций (что не мешает затем получать графики).
В математическом моделировании все системы делят на системы с сосредоточенными параметрами и системы с распределенными параметрами. Поведение во времени систем первого вида описывается обыкновенными дифференциальными уравнениями (задача Коши). Поведение систем второго типа описывают дифференциальными уравнениями в частных производных. Рассмотрим систему с сосредоточенными параметрами. Для описания динамики такой системы используется система дифференциальных уравнений, которая, в общем случае может быть представлена так:
где F - система функций, x - вектор переменных состояния, p(i) - вектор производных по t от x порядка i . К этим уравнениям необходимо добавить еще систему начальных условий. Путем соответствующей замены переменных (и ценой увеличения числа уравнений) последнюю систему всегда можно преобразовать так, что она будет содержать производные только лишь первого порядка. С учетом начальных условий задача будет иметь следующий вид: F(t, x, p) = 0 (1) x(0) = x(0) . Здесь p - вектор первых производных: p = ¶x/¶t . Решением задачи является набор функций x(t). Для численного решения задачи могут быть использованы т.н. неявные методы. Довольно часто систему уравнений (1) удается разрешить относительно производных, тогда задача принимает следующий вид:
Если задача решается численно, всегда задан некоторый конечный интервал интегрирования [0,T] . Для построения алгоритма используется дискретизация по t и конечные разности. Результат численного решения Задачи Коши имеет табличную форму представления искомых функций (что не мешает затем получать графики).
Поиск по сайту: |

 .
. метод сходится к решению.
метод сходится к решению. ,
, ,
, .
. .
.
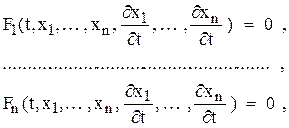 (1)
(1)
 (2)
(2) ,
,
 , (3)
, (3)
 ,
, (2)
(2)